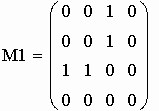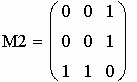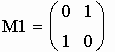Основные источники:
1. Дискретная математика : учебник для студ. учреждений сред. проф. образования / М.С.Спирина, П.А.Спирин. —. 7-е изд., стер. — М.: Издательский центр «Академия», 2012. —. 368 с.
2. М.С.Спирина, П.А.Спирин. Дискретная математика. Изд-во Академия/Academia", 2010 г.
Дополнительные источники:
1. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики. М. Форум - инфри - м 2003 г. 2. Горбатов В.А. Основы дискретной математики. М. Наука 1986 г. 3. Кузнецов О.П., Адельсон - Вильский Г.М. Дискретная математика для инженера. Энергоатомиздат, 1998 г. 4. Нефедов В.Н., Осипова В.А. Курс дискретной математики. М. Издательство МАИ 1992 г. 5. Яблонский С.В. Введение в дискретную математику. М. Наука, 1986 г., 384с.
Интернет ресурсы:
1. М.М. Арсланов, И.Ш. Калимуллин. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.http://www.ksu.ru/f5/k2/bin_files/logika!13.pdf
2. Гиндикин С.Г. Алгебра логики в задачах. Электронная библиотека Московского государственного университета. http://lib.mexmat.ru/books/1383
Раздел 2. Теория графов.(24ч.)
Тема 2.1. Основные понятия и определения графа и его элементов. Самостоятельная работа №13.
Тема: Изучить правило игры, придуманные Гамильтоном в XIX веке, задачу о коммивояжере - задачу математического программирования.
Время выполнения задания – 2ч.
Цель работы: Закрепление знаний по правило игры, придуманные Гамильтоном в XIX веке, а также по задаче о коммивояжере - задаче математического программирования.
Напишите реферат по теме самостоятельной работы и ответе на контрольные вопросы:
Вопросы для самоконтроля:
1. Какого правило игры, придуманные Гамильтоном в XIX веке .
2. Что такое коммивояжер?
3. Каким способом решается задачи математического программирования?
4. Что такое оптимальное решение задачи математического программирования?
Рекомендуемая литература:
Основные источники:
1. Дискретная математика : учебник для студ. учреждений сред. проф. образования / М.С.Спирина, П.А.Спирин. —. 7-е изд., стер. — М. : Издательский центр «Академия», 2012. —. 368 с.
Дополнительные источники:
1. Вентцель Е.С. «Исследование операций, задачи, принципы, методология» М. Наука 1988 г. 5. Кузнецов О.П., Адельсон - Вильский Г.М. Дискретная математика для инженера. Энергоатомиздат, 1998 г. 6. Нефедов В.Н., Осипова В.А. Курс дискретной математики. М. Издательство МАИ 1992 г. 7. Нефедов Ф.А. Дискретная математика для программистов. СПб – Питер. 2001 г.
Интернет ресурсы:
1. М.М. Арсланов, И.Ш. Калимуллин. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.http://www.ksu.ru/f5/k2/bin_files/logika!13.pdf
2. Гиндикин С.Г. Алгебра логики в задачах. Электронная библиотека Московского государственного университета. http://lib.mexmat.ru/books/1383
3. Решение задачи о коммивояжере edu.Nstu.Ru/courses/mo_tpr/files/3.4.Html Тема 2.2. Операции над графами.
Самостоятельная работа №14.
Тема: Операции над графами. Кольцевая сумма.
Время выполнения задания – 2ч.
Цель работы: Закрепление знаний и умений по операциям над графами.
Теоретический материал.
Бинарные операции
Во второй части работы реализуются основные бинарные операции над графами: объединение графов, пересечение графов, кольцевая сумма графов, декартово произведение графов.
1. Выполняем генерацию матриц М1, М2 смежности неориентированных помеченных графов G1, G2.
алгоритм генерации матриц:
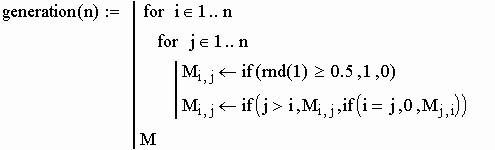
генерация матриц смежности М1 и М2:
|
|
|
|
|
|
m2 - вектор с номерами вершин матрицы М2; номера вершин матрицы М2 можно задавать любые.
2. Выполняем операцию объединения графов G1 и G2, заданных матрицами М1 и М2 соответственно.
алгоритм объединения графов:
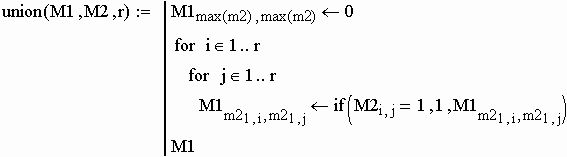
r - размерность второй матрицы (M2).
Объединим матрицы М1 и М2:
|
|
|
|
объединенная матрица М:
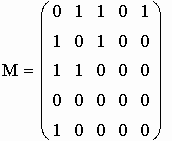
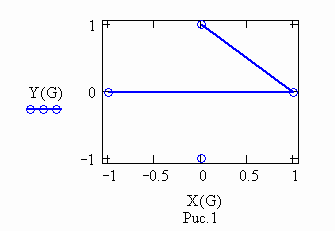
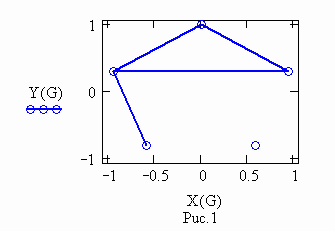
счет вершин в графе ведется по часовой стрелке от левой вершины
граф матрицы М1 вершины имеют номера |
граф матрицы М2 вершины имеют номера |
|
|
|
|
граф
объединенной матрицы М
3. Выполняем операцию пересечения графов G1 и G2, заданных матрицами М1 и М2 соответственно.
|
|
|
|
m2 - вектор с номерами вершин матрицы М2; номера вершин матрицы М2 можно задавать любые.
Алгоритм пересечения графов:
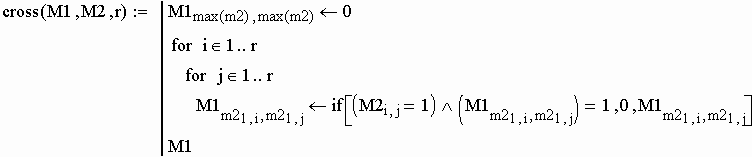
r - размерность второй матрицы (M2). Матрица пересечения графов G1 и G2
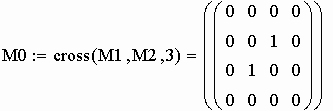
4. Выполняем операцию кольцевой суммы графов G1 и G2, матрицы которых М1 и М2 соответственно (кольцевая сумма аналогична сложению по модулю 2).
Алгоритм кольцевой суммы графов:
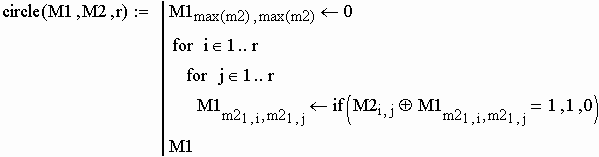
r - размерность второй матрицы (M2).
Матрица кольцевой суммы графов G1 и G2
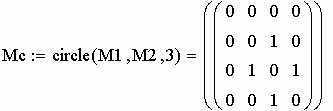
граф матрицы М1 вершины имеют номера |
граф матрицы М2 вершины имеют номера |
|
|
|
|
граф матрицы пересечения графов |
граф матрицы кольцевой суммы графов |
|
|
|
|
5. Задаем графы, содержащие два ребра. Выполним операцию декартова произведения графов.
|
|
|
|
|
|
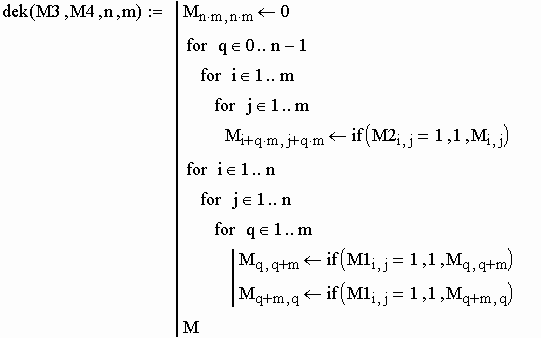
n,m - размерности матриц.
М - матрица декартова произведения графов G1 и G2.
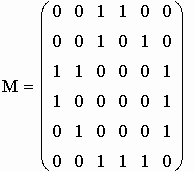
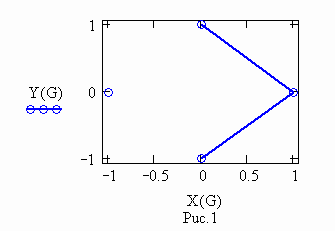
Два исходных графа
|
|
|
|
их декартово произведение
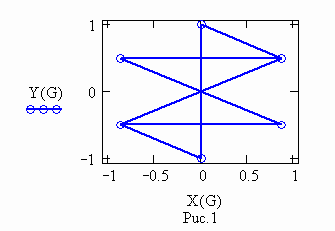
Вопросы для самоконтроля:
1. Дайте определения графу.
2. Что такое «вершина» графа?
3. Что такое «ребро» графа?
4. Какие виды графа знаете?
5. Что такое «кольцевая сумма»?
Рекомендуемая литература: