Основные источники:

1. Дискретная математика : учебник для студ. учреждений сред. проф. образования / М.С.Спирина, П.А.Спирин. —. 7-е изд., стер. — М. : Издательский центр «Академия», 2012. —. 368 с.

2. М.С.Спирина, П.А.Спирин. Дискретная математика. Изд-во Академия/Academia", 2010 г.

Дополнительные источники:

1. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики. М. Форум - инфри - м 2003 г. 2. Горбатов В.А. Основы дискретной математики. М. Наука 1986 г. 3. Карпов В.Г., Мощенский В.А. Математическая наука и Дискретная математика. Минск. Винца школа 1977 г. 4. Кузнецов О.П., Адельсон - Вильский Г.М. Дискретная математика для инженера. Энергоатомиздат, 1998 г. 5. Нефедов В.Н., Осипова В.А. Курс дискретной математики. М. Издательство МАИ 1992 г. 7. Нефедов Ф.А. Дискретная математика для программистов. СПб – Питер. 2001 г.

Интернет ресурсы:

1. М.М. Арсланов, И.Ш. Калимуллин. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.http://www.ksu.ru/f5/k2/bin_files/logika!13.pdf

2. Гиндикин С.Г. Алгебра логики в задачах. Электронная библиотека Московского государственного университета. http://lib.mexmat.ru/books/1383

Самостоятельная работа №10.

Тема: Свойства биноминальных коэффициентов. Треугольник Паскаля.

Время выполнения задания – 2ч.

Цель работы: Закрепление знаний и умений по свойствам биноминальных коэффициентов.

Теоретический материал.

Рассмотрим формулы, которые позволяют достаточно легко и быстро решать большой класс задач. Например, если требуется найти коэффициент, который стоит перед   многочлена  . Для решения достаточно раскрыть все скобки, перемножить, привести подобные и получить ответ. Как видно, это достаточные долгие и нудные вычисления. В данном пункте приводятся формулы, по которым получается сразу ответ, это так называемый Бином Ньютона.

Хорошо известны следующие школьные формулы:

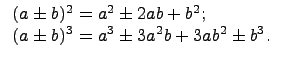
Поставим вопрос о том, можно ли эти формулы обобщить на произвольную натуральную степень   , т.е. рассмотрим следующий многочлен относительно   и   и степени   :

Данное равенство легко получить, раскрыв все скобки и приводя подобные члены. Здесь коэффициенты A_i , где i=1, 2, …, n, являются неизвестными и требуются определения.

Возникает вопрос, а каким образом, каким способом можно найти данные коэффициенты?

Ответ на этот вопрос дает Бином Ньютона:

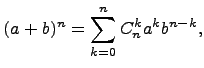
где

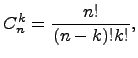
здесь   и по определению  . Коэффициенты   называются биномиальными.

Это равенство можно доказать методом математической индукции.

Приравнивая коэффициенты при одинаковых степенях, получаем выражения для коэффициентов:

Рассмотрим еще один способ получения коэффициентов   в разложении   - это треугольник Паскаля.

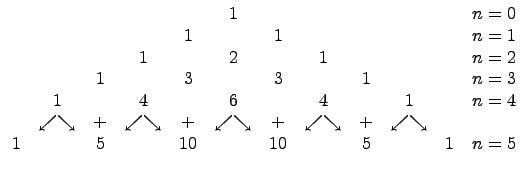
Опишем алгоритм построения данного треугольника. Каждая строка треугольника соответствует конкретной степени   многочлена, значения в строке соответствуют коэффициентам в разложении. Треугольник строится сверху вниз, т.е. от многочлена нулевой степени, каждый раз увеличивая степень на единицу. Стрелками показано какие операции выполняются, т.е. сносятся каждые числа и складываются соседние.

Далее выписывается многочлен данной степени   и расставляются по порядку значения из  -ой строки треугольника.

Пример: Найти разложение:

Решение. В данном примере:   ,   и   , т.е. нужно взять четвертую строку треугольника (где справа стоит   ).

Выписываем разложение с неопределенными коэффициентами:

подставляем вместо   и   , получаем

Теперь берем значения из четвертой строки треугольника и подставляем их поочереди вместо коэффициентов:

Ответ: 

Здесь прослеживается реккурентная связь между коэффициентами. Получаем, что если известны коэффициенты для многочлена (n-1) -ой степени, тогда для многочлена   -ой степени они находятся простым суммированием.

Получается, что элемент, стоящий в   -ой строке ( n=0, 1, 2, … ), и в   -ом столбце ( k=0, 1, 2, …, n ) определяется по формуле

т.е. это будет связь треугольника Паскаля с биномиальными коэффициентами.

Рассмотрим пример, про который говорилось в начале пункта: найти коэффициент, который стоит перед   многочлена (2x+1,5)¹¹?

Решение.Используя бином Ньютона, получаем:

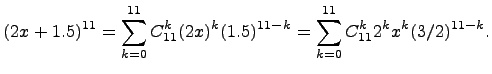
Степень, равная   -и, у   будет при   , получаем, что коэффициент при   равен

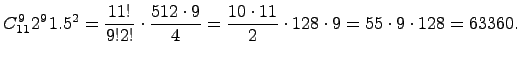
Вопросы для самоконтроля:

1. Дайте определение «треугольник Паскаля».

2. Что такое биноминальные коэффициенты?

3. Что такое бином Ньютона?

Рекомендуемая литература:

Основные источники:

1. Дискретная математика : учебник для студ. учреждений сред. проф. образования / М.С.Спирина, П.А.Спирин. —. 7-е изд., стер. — М. : Издательский центр «Академия», 2012. —. 368 с.

2. М.С.Спирина, П.А.Спирин. Дискретная математика. Изд-во Академия/Academia", 2010 г.

Дополнительные источники:

1. Вентцель Е.С. «Исследование операций, задачи, принципы, методология» М. Наука 1988 г. 2. Горбатов В.А. Основы дискретной математики. М. Наука 1986 г. 3. Нефедов Ф.А. Дискретная математика для программистов. СПб – Питер. 2001 г.

Интернет ресурсы:

1. М.М. Арсланов, И.Ш. Калимуллин. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.http://www.ksu.ru/f5/k2/bin_files/logika!13.pdf

2. Гиндикин С.Г. Алгебра логики в задачах. Электронная библиотека Московского государственного университета. http://lib.mexmat.ru/books/1383

Самостоятельная работа №11.

Тема: Применение комбинаторики при вычислении дискретных математических структур.

Время выполнения задания – 2ч.

Цель работы: Закрепление знаний и умений по применению комбинаторики при вычислении дискретных математических структур

Теоретический материал.

(См. «теоретический материал» из СР №9)

Решите задачи:

1. Сколько существует способов поставить на книжную полку в беспорядке собрание сочинений, состоящий из 7 томов?

2. Из цифр 3, 4, 5, 6 составлены четырехзначные числа. Сколько вариантов таких чисел можно найти, если среди найденных четверок нет чисел, заканчивающихся на 36?

3. Сколько всевозможных кортежей длиной 7 можно составить из слова «кислота»?

4. Сколькими способами можно построить кортежи из букв слова «грамматика»?

5. Сколькими способами можно поставить на полку четырехтомник Пушкина, двухтомник Ахматовой и трехтомник Лермонтова, так, чтобы книги каждого автора стояли рядом?

6. На полке стоят 10 книг, 5 из них – собрание сочинений Л.Н.Толстого. Сколько существует вариантов расстановки книг на полке при условии, что все 5 томов Л.Н.Толстого должны стоять рядом?

7. Сколькими способами можно устроить на летную практику 10 студентов на 3 предприятия города?

8. Придумайте и решите аналогичную задачу.

Вопросы для самоконтроля:

1. Дайте определение комбинаторики.

2. Что такое размещение?

3. Что такое перестановки?

4. Что такое сочетание?

Рекомендуемая литература: