16.Реальное интегрирующее динамическое звено, как упрощенная математическая модель движения судна.

Основываясь на втором законе Ньютона, в общем виде движение подвижного объекта, оснащенного неким движителем, может быть описано формулой:

, где I – момент инерции создаваемый движителем, - угловая скорость, L - сумма моментов сил, действующих на корпус судна в результате перекладки пера руля и внешних факторов. С другой стороны, , здесь - гидродинамические коэффициенты, зависящие от самой конструкции корпуса судна, шага винта, обрастания и т.д. , и представляют собой сложные эмпирические зависимости, которые рассчитываются при испытаниях головной модели в серии.

- угол перекладки пера руля

- скорость изменения положения ДП судна относительно вертикальной оси

- суммарный момент сил внешних факторов, действующих на судно.

Учитывая, что , получаем

Используем преобразование Лапласа и разделим все уравнения на , в результате получим:

Обозначим :

- постоянная времени судна, описывает инерционные характеристики судна.

- коэффициент усиления по управлению. Описывает эффективность воздействия пера руля.

- коэффициент усиления по внешнему воздействию.

Подставим в уравнение, получим:

- основное уравнение для получения передаточной функции.

1. Рассмотрим случай движения судна при и (движение судна при нормальных условиях). - передаточная функция по управляющему воздействию.

2. Рассмотрим движение судна при и (прямолинейное движение судна при воздействии внешних факторов)

- передаточная функция по внешнему фактору.

, где

- усилительное звено

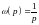- интегрирующее звено

- апериодическое звено

17.Система автоматического управления курсом судна. Режимы работы, структурные схемы, графики переходных процессов.

Различают несколько режимов работы современного авторулевого:

1. Ручное управление

2. Полуавтоматическое (следящий режим)

3. Автоматическое управление

1. Рассмотрим ручное управление

ИД – исполнительный двигатель

РМ – рулевая машина

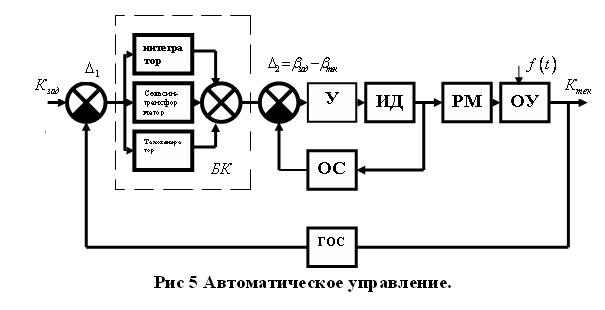
18.Принцип действия блока коррекции системы автоматического управления курсом судна.

Качество регулирования определяется блоком коррекции:

1. Интегратор учитывает (компенсирует) снос судна из-за действия ветра и течения.

2. Тахогенератор влияет на перерегулирование

3. Сельсин-трансформатор вырабатывает сигнал, пропорциональный углу поворота штурвала.

Таким образом качество переходного процесса определяется КОС, интегратором и тахогенератором.

На выходе блока коррекции сигнал представлен следующей формулой:

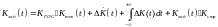
Для подстройки авторулевого к текущим условиям плавания необходимо использовать 3 коэффициента:

19.Устойчивость сау. Алгебраические критерии устойчивости линейных сау. Критерий Рауса-Гурвица.

Устойчивость САУ – способность системы самостоятельно приходить к последующему установившемуся состоянию после приложения воздействия, которое её вывело из равновесия.

Определение, является ли система устойчивой при заданных параметрах, возможно различными методами, которые основываются на установлении факта отрицательности вещественных корней характеристического уравнения без нахождения их значения.

Алгебраический критерий позволяет установить по результатам алгебраических действий над коэффициентами характеристического уравнения устойчива САУ или нет.

1873 год – Раус впервые предложил этот алгебраический критерий

1875 год – Гурвиц улучшил этот критерий, сократив его формулировку.

Определение критерия.

Вещественные части корней характеристического уравнения будут отрицательны, если все коэффициенты и диагональные миноры главного определителя будут положительны.

, где n – порядок характеристического уравнения.

Главный определить характеристического уравнения составляется так, что по главной диагонали выписываются коэффициенты уравнения, начиная с в возрастающем порядке до . От каждого коэффициента главной диагонали по вертикали вверх выписываются коэффициенты с возрастающими, а вниз с убывающими индексами.

Места в матрице с индексами больше n и меньше 0 заполняются нулями.