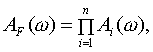10. Сформулируйте критерий устойчивости Михайлова

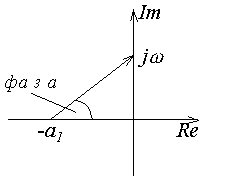
Для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова при изменении от 0 до начинался на вещественной оси в точке и проходил последовательно против часовой стрелки n квадрантов, не обращаясь в ноль и стремясь к в n-ом квадранте.

Доказательство

Утверждение основано на расположении годографа Михайлова на комплексной плоскости, поэтому проанализируем, как связаны корни характеристического уравнения с видом F(j ). Поскольку полином (4.16) можно представить как произведение простых сомножителей

F(p) = (p - ) (p - ),

характеристический комплекс (4.17) также принимает вид:

F(j ) =

Его можно представить в форме

Из выражений (4.18) и (4.21) следует, что

Если характеристическое уравнение системы содержит чисто мнимые корни, то, как следует из (4.22), при определенном значении частоты , так как при этом один из сомножителей обратится в ноль. В случае устойчивой системы корни расположены только в левой полуплоскости плоскости корней и не могут быть чисто мнимыми, следовательно, в ноль годограф Михайлова не обращается.

Определим теперь угол поворота вектора F(j ) при изменении частоты от 0 до . Поскольку , в соответствии с (4.23), есть сумма отдельных , то рассмотрим угол поворота каждого сомножителя выражения (4.20).

Корень характеристического уравнения вещественный отрицательный; Соответствующий сомножитель в (4.20) имеет вид: ( ).

Рис.4.9. Элементарный вектор, соответствующий устойчивому вещественному корню

Изобразим этот элементарный вектор на комплексной плоскости; при изменении от 0 до его вещественная часть остается неизменной и равна , а мнимая часть возрастает до бесконечности. Как видим, угол поворота элементарного вектора, соответствующего устойчивому вещественному корню, равен

Если корень характеристического уравнения вещественный положительный, , то угол поворота элементарного вектора равен

Рассмотрим теперь пару устойчивых комплексно - cопряженных корней и соответствующий им угол поворота произведения

Рис.4.10. Векторы, соответствующие устойчивым комплексно - сопряженным корням

У векторов А, В начальные фазы одинаковы по модулю ( ), но имеют противоположные знаки. При изменении от 0 до один вектор поворачивается на угол, равный , а второй - на угол

Суммарный угол поворота для пары устойчивых комплексно - сопряженных корней равен

Если комплексно - сопряженные корни имеют положительную вещественную часть, то суммарный угол поворота равен

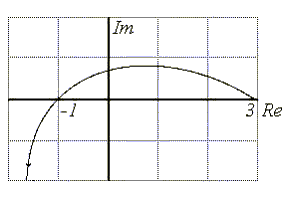
Таким образом, в устойчивой системе каждый из n корней даст приращение фазы , а общий угол поворота F(j ) согласно (4.23) равен , что и требовалось доказать. Вид годографа Михайлова для устойчивых и неустойчивых систем третьего порядка приведен на рис.4.11.

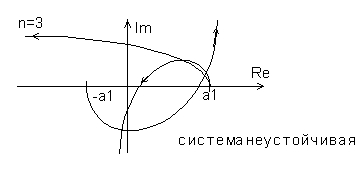
Рис.4.11. Годограф Михайлова для устойчивой и неустойчивой систем

Система будет находиться на границе устойчивости, если годограф Михайлова при некотором значении частоты обращается в ноль, то есть при выполнении условия:

Здесь частота ₀ - есть частота незатухающих колебаний системы.

Пример 4.5.

Вид годографа Михайлова неустойчивой системы шестого порядка:

Пример 4.6.

Вид годографа Михайлова системы третьего порядка в зависимости от вличины коэффициента передачи:

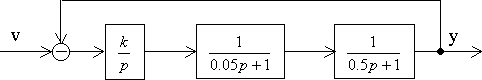
Пример 4.7.

Оценить устойчивость системы, структурная схема которой имеет вид:

Определим передаточную функцию системы

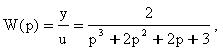
и запишем ее характеристический полином

Заменой p на перейдем к выражению для годографа Михайлова

которое представим в форме

С целью построения годографа Михайлова вычислим значения вещественной и мнимой части при конкретных значениях частоты и занесем их в таблицу.

Рис.4.13. Годограф Михайлова для исследуемой системы

По данным таблицы построим годограф Михайлова Как видим, он проходит последовательно три квадранта, не обращаясь в ноль и стремясь к бесконечности в третьем квадранте. Следовательно, исследуемая система устойчива.