Что такое «Кривая разгона»
Кривой разгона называют процесс изменения во времени выходной переменной, вызванный ступенчатым входным воздействием. Кривая разгона служит для определения динамических свойств объекта.
Запаздывание объекта выражается в том, что его выходная величина начинает изменяться не сразу после нанесения возмущения, а только через некоторый промежуток времени, называемым временем запаздывания.
Под постоянной времени объекта понимается время, в течение которого выходная величина достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости ее изменения в начальный момент времени.
Коэффициент передачи объекта представляет собой изменение выходной величины объекта при переходе из начального в новое установившееся состояние, отнесенное к изменению возмущения на входе [1].
Снятие кривой разгона предусматривает нанесение на объект ступенчатого возмущения путем энергичного изменения степени открытия проходного сечения регулирующего органа, при этом отмечают величину и момент нанесения возмущения. Изменения выходной величины регистрируют до тех пор, пока объект не примет установившееся значение.
Кривая разгона отличается от переходной характеристики тем, что амплитуда «скачка» может быть произвольной, в то время как переходная характеристика есть реакция объекта управления на единичный скачок по управляющей переменной [2].
Кривая разгона получается пересчетом безразмерной кривой разгона по формулам
t = Mt . tб
Δy = My . Δyб
где t – реальное время,
tб – безразмерное время,
Mt – масштаб времени,
My – масштаб регулируемой переменной,
Δy – изменение регулируемой переменной в натуральных единицах,
Δyб – изменение регулируемой переменной в безразмерном виде
Дать определение передаточной функции
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ линейной стационарной системы управления (системы автоматич. регулирования) - Лапласа преобразование отклика системы на воздействие единичной импульсной функции (дельта-функции) 6 (г) при нулевых условиях в момент t=0 (сам этот отклик наз. функцией веса, импульсной переходной функцией или импульсной характеристикой системы).
Эквивалентное определение: ПЕРЕДАТОЧНАЯ ФУНКЦИЯ - есть отношение изображений по Лапласу (см. Операционное исчисление).выходного и входного сигналов с нулевыми начальными данными. П. ф. представляет собой дробно-рациональную функцию W(p).комплексного переменного р;она является коэффициентом в линейном соотношении
(1)
связывающем изображение по Лапласу U(р).входа системы (воздействия, управления) и(t).и изображение по Лапласу Y(р).выхода системы (отклика, реакции) y(t).с нулевыми начальными значениями. В теории управления соотношение (1) принято изображать графически (см. рис.).
Пусть, напр., система управления описывается линейным обыкновенным дифференциальным уравнением с постоянными коэффициентами
(2)
(в реальных системах, как правило,
).
Тогда
(3)
Это же выражение можно получить, если, используя операторную форму записи уравнения (2) с помощью оператора дифференцирования р
определить
П. ф. как отношение входного оператора
системы В(р) к собственному оператору
системы (р). П. ф. (3) системы (2) допускает
следующее толкование: если выбрать
управление
,
где s - комплексное число такое, что
,
то линейное неоднородное уравнение
(2) имеет частное решение
.
П. ф. не следует путать с переходной функцией, к-рая представляет собой отклик системы на воздействие единичной ступенчатой ф у н к ц и и
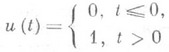
при нулевых начальных условиях.
П. ф. является одним из основных понятий теории линейных стационарных систем управления. Она не зависит от характера приложенных к системе управляющих воздействий, а определяется лишь параметрами самой системы и дает тем самым ее динамич. характеристику. Особую роль в теории управления играет функция W(iw) чисто мнимого аргумента, наз. амплитудно-фазовой, или частотной, характеристикой системы. Понятие П. ф. обобщается и на линейные системы управления иных типов (матричные, нестационарные, дискретные, с распределенными параметрами и др.).