Критерии оценивания
Условие равновесия шайбы 2
Уравнение для границ областей равновесия 2
Определение границ областей равновесия в I случае (пружина) 2
График областей равновесия в I случае 1
Определение границ областей равновесия во II случае (резинка) 2
График областей равновесия во II случае 1
Задача 3. Сложный конденсатор
(Козел С.)
С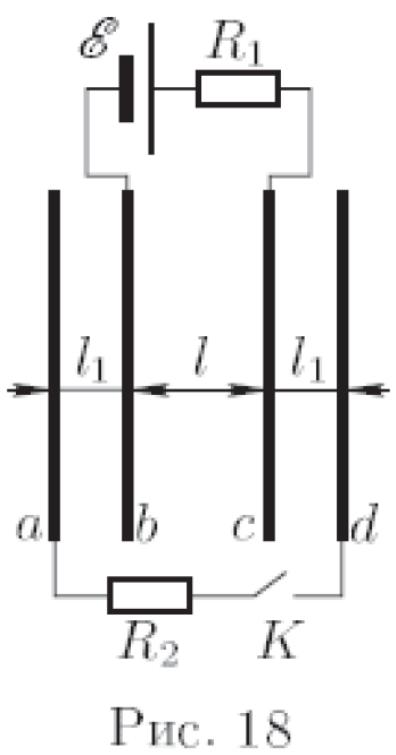
ложный
конденсатор состоит из четырёх одинаковых
пластин площадью 
каждая, расположенных параллельно друг
другу (рис. 18).
Расстояние между средними пластинами
и
равно
.
Расстояние между пластинами
и
,
и
равно
.
Пластины
и
подключены к идеальному источнику
напряжения с
через резистор
.
В начальном состоянии ключ 
разомкнут.
1. Нарисуйте эквивалентную схему сложного конденсатора после замыкания ключа и найдите его ёмкость .
2. Какое количество теплоты 
выделится на резисторах
и
(в сумме) при замыкании ключа
.
Электрическая постоянная
.
Указание. Воспользуйтесь законом сохранения энергии.
Решение
П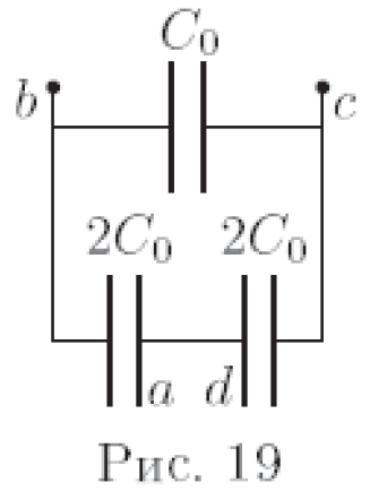
ервоначальная
ёмкость конденсатора (то есть ёмкость
между пластинами
и
)
равна
После замыкания ключа
и установления нового равновесного
состояния все токи обращаются в ноль
и, следовательно, разность потенциалов
между крайними пластинами также
обращается в ноль. Эквивалентная схема
сложного конденсатора имеет вид,
показанный на рисунке 19. Ёмкость
сложного конденсатора равна
.
Следовательно, при замыкании ключа
ёмкость изменилась на
.
Применим закон сохранения энергии:
где
—
работа батареи.
где
—
заряд, протёкший через батарею после
замыкания ключа
.
Изменение
электрической энергии сложного
конденсатора равно:
Таким образом, количество теплоты, выделившейся в схеме на обоих резисторах, равно:
Критерии оценивания
Эквивалентная схема сложного конденсатора 1
Расчёт ёмкости сложного конденсатора 2
Применение закона сохранения энергии 2
Определение работы батареи 2
Определение изменения электростатической энергии 1
Формула для количества теплоты 1
Численное значение 1
Задача 4. Минимальная скорость протона
(Соболев М.)
1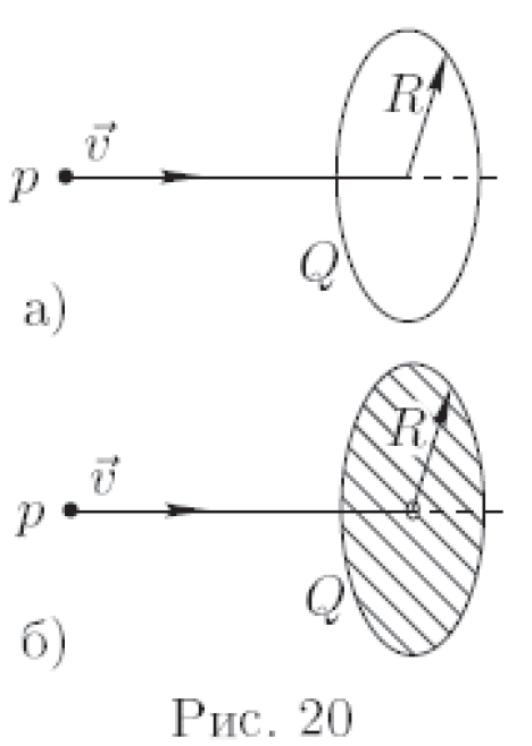
. Тонкое
кольцо радиусом 
однородно заряжено зарядом 
(рис. 20 а). Какую минимальную скорость 
нужно сообщить протону, находящемуся
вдали от кольца, чтобы он пролетел по
оси кольца через его центр?
2. Пусть теперь заряд равномерно распределён по поверхности тонкого диска радиуса (рис. 20 б). В центре диска имеется небольшое отверстие. Какую минимальную скорость нужно сообщить протону в этом случае, чтобы он пролетел через отверстие в диске?
Элементарный заряд 
,
масса протона 
,
электрическая постоянная
.
Решение
1. По принципу суперпозиции потенциал
в центре кольца равен
Потенциальная энергия
протона в центре кольца:
По закону сохранения энергии
.
Тогда
2. Найдём потенциал
в центре равномерно заряженного диска.
Поверхностная плотность заряда на диске
.
Рассмотрим элементарное кольцо радиусом
и толщиной
.
Заряд этого кольца равен
Потенциал, создаваемый элементарным кольцом в его центре, равен
Отсюда потенциал в центре диска:
Как видно,
.
Следовательно,
,
и тогда
