6.4 Жесткость тонкостенных стержней замкнутого профиля при свободном кручении
Для
того, чтобы определить угол закручивания
используем равенство
,
где
- потенциальная энергия деформация
элемента длиной
,
- работа моментов
,
вызвавших деформацию элемента, которой
является чистый сдвиг с напряжением
.
Энергия деформации, сосредоточенная в
точке (плотность энергии) при чистом
сдвиге будет
,
тогда для элемента стержня размером
энергия имеет вид
.
Проинтегрировав по замкнутому контуру
и использовав формулу Бредта, получим
значение потенциальной энергии
.
Работу
момента получим как площадь диаграммы,
определяющей связь между крутящим
моментом и углом закручивания по закону
Гука
.
Используя равенство
,
получим
,
где
является жесткостью замкнутого сечения
при свободном кручении.
В
частном случае, жесткость круглого
тонкостенного сечения равна
.
Для
замкнутого квадратного сечения, при
:
.
Для
такого же стержня открытого сечения
(если в произвольной стенке имеется
разрез), при
,
получим
Их отношение
.
Например,
при
получим
.
Таким образом, при одинаковых условиях углы закручивания замкнутого сечения будут в 300 раз меньше, чем у стержня с прорезью. Также распределения касательных напряжений будут существенно различаться, а деформация открытого профиля будет сопровождаться сильной депланацией.
Пример №1
Сравнить
жесткость и прочность открытого и
замкнутого круглого тонкостенного
профиля при кручении (рис) для
Р
ешение
Характеристики
жесткости и прочности открытого профиля
вычисляется по формулам
и
Характеристики
жесткости и прочности замкнутого профиля
вычисляется по формулам
и
Тогда
и
Пример №2
П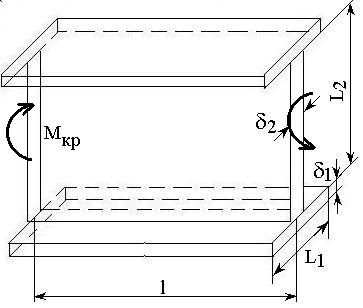
роверить
выполнение условия прочности при
кручении стержня двутаврового профиля
и определить максимальный угол
закручивания возникающий при этом
Решение:
Момент сопротивления при кручении стержней открытого профиля определяется по формуле
Тогда
и условие прочности не выполнено.
Геометрическая
характеристика жесткости сечения
определяется по формуле
,
а угол закручивания равен
.
Такое большое значение угла означает
плохую работу стержней тонкостенного
открытого поперечного сечения на
кручение.
Конспект по сопротивлению материалов III-ий семестр. Автор: к.т.н., доц. А.В. Терентьев