II) консольная балка
Для
консольной балки (см. рис.5.8) для
,
1) записать выражения и построить эпюры поперечных сил и изгибающих моментов
2) проверить выполнение условий прочности по нормальным и касательным напряжениям для сечения в виде двух швеллеров № 10
Решение:
Совмещаем начало координат с правым свободным концом балки (в этом случае не нужно определять реакции, возникающие в заделке)
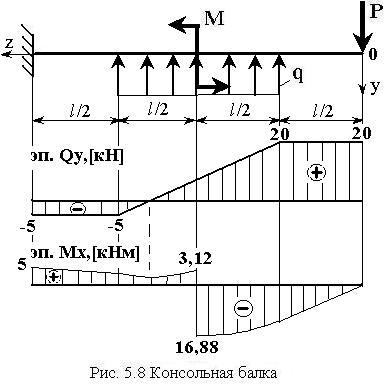
1. Выражения для поперечной силы и изгибающего момента
а) по участкам
EMBED
Equation.3
б) в одну строку
Заносим значения внутренних усилий в характерных точках и строим эпюры
Определяем
координату на третьем участке
,
где поперечная сила равна нулю:
,
при этом
имеет минимум.
2) Проверка выполнения условий прочности
Максимальное
значение изгибающего момента:
,
а максимальное значение поперечной
силы:
.
Для
одного швеллера № 10:
.
=>
условие прочности по нормальным
напряжениям выполнено.
условие прочности по касательным напряжениям выполнено.
5.7 Универсальное уравнение изогнутой оси
В
ертикальные
перемещения центров тяжестей сечений
стержня
называется
прогибом
стержня, а угол между касательной к
искривленной оси балки и горизонталью
называется
углом
поворота
поперечного сечения (см. рис. 5.9). Функция
называется
уравнением
упругой линией
или линией
прогибов
балки, при этом графически строится
изогнутая
ось (упругая линия)
стержня. Для выбранной системы координат
положительным
является перемещение,
направленное вниз, а угол
положителен при повороте против часовой
стрелки. В рамках технической теории
изгиба считаем, что
.
Из
геометрии следует, что
.
Относительная
продольная деформация меняется по
высоте сечения по закону:
,
тогда
.
Если
,
то радиус кривизны
и изогнутая ось направлена выпуклостью
вниз, если
- выпуклостью вверх.
Точное
математическое выражение для кривизны
любой плоской кривой
в случае малых изгибных деформаций
имеет
вид
.
Сравнивая
математическое и физическое выражения
для кривизн, получим что
.
Произведя
двойное дифференцирование полученного
выражения с учетом дифференциальных
зависимостей между внутренними усилиями
при изгибе, получим
.
Полагая
изгибную жесткость стержня постоянной
,
выражения для прогибов, изгибающих
моментов и поперечных сил получим
интегрированием данного выражения:
,
,
,
.
В
данных выражениях константы интегрирования
определяют прогиб, угол поворота,
изгибающий момент и поперечную силу в
начале координат. Они называются
начальными
параметрами.
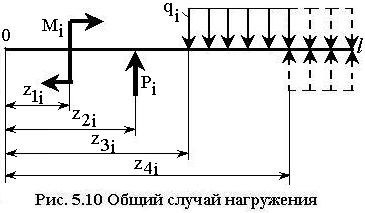
В случае действия произвольного количества нагрузок разного типа (рис. 5.10) полученные выражения можно обобщить
,
,
,
Выражение для прогиба называется универсальным уравнением. В данные выражения должны быть включены все нагрузки (внешние и реактивные), действующие на стержень, кроме сосредоточенных нагрузок, действующих на конце стержня, противоположном началу координат. Каждая- нагрузка учитывается в данных выражениях только при превышении осевой координаты указанного значения. В случае если распределенная нагрузка действует только на части длины стержня, то ее необходимо достроить от конца ее действия до конца стержня противоположного началу координат и учесть данное слагаемое в качестве отдельной нагрузки противоположного направления.
Неизвестные начальные параметры определяются из граничных условий, составленных для левого и правого концов стержня. В случае наличия у стержня промежуточных опор для определения действующих на них реактивных усилий составляются дополнительные условия отсутствия прогибов на них, а неизвестная реакция на опоре учитывается в качестве слагаемого соответствующего силе. При построении эпюр поперечных сил и изгибающих моментов в местах действия соответствующих сосредоточенных усилий происходят скачки. Кроме того, следует проверять выполнение дифференциальных соотношений между внутренними усилиями. Вследствие степенной зависимости от осевой координаты эпюры прогибов и углов поворота являются гладкими функциями, не имеющими скачков и изломов. В точках, где сила равна нулю, момент имеет экстремум, а в точках, где момент равен нулю, кривизна изогнутой оси равна нулю, т.е. имеется точка перегиба.