3.4 Содержание отчёта
3.4.1 Таблица истинности системы ПФ.
3.4.2 Минимизирующие карты Карно.
3.4.3 Аналитическая запись минимизированных функций в заданном базисе.
3.4.4 Функциональные схемы, реализующие систему ПФ.
Электрические принципиальные схемы в среде Proteus.
3.4.8 Выводы.
Контрольные вопросы
Дать определение дешифратора. Привести условное обозначение микросхемы дешифратора на схемах. Пояснить назначение выводов и принцип работы.
Привести схемотехническое представление дешифратора и его формулу, таблицу истинности. Что такое полный и неполный дешифратор?
Построить схему наращивания дешифраторов для получения 16 выходов, используя дешифраторы 2-4.
Построить схему на дешифраторах совместно со схемами ИЛИ для воспроизведения логических функций
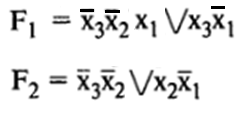
Назвать примеры применения дешифраторов.
Что такое шифратор? Полный, неполный шифратор, условное обозначение, назначение выводов.
Дать определение приоритетного и двоичного шифратора, объяснить принцип работы.
Что такое указатель старшей единицы? Пояснить принцип работы и применение.
4 Практическая работа № 4. Компараторы. Схемы контроля. Сумматоры.
4.1 Цель работы
4.2 Сведения из теории
Цифровые компараторы (от английского compare – сравнивать) выполняют сравнение двух чисел А, В одинаковой разрядности, заданных в двоичном или двоично-десятичном коде. В зависимости от схемного исполнения компараторы могут определять равенство А=В или неравенства А<В, А>В. Результат сравнения отображается в виде логического сигнала на одноименных выходах.
Цифровые компараторы применяются для выявления нужного числа в цифровых последовательностях, для отметки времени в часовых приборах, для выполнения условных переходов в вычислительных устройствах, а также в адресных селекторах.
В сериях цифровых элементов обычно имеются компараторы с тремя выхо- выходами: "равно", "больше" и "меньше" (рис. 2.16). Для краткости записей в индексе выходных функций указывается только слово А.
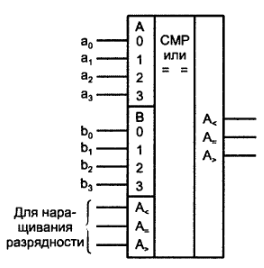
Рисунок 4.1 - Условное обозначение компаратора с 3 выходами
Устройства сравнения на равенство строятся на основе поразрядных опера- операций над одноименными разрядами обоих слов. Слова равны, если равны все одноименные их разряды, т. е. если в обоих нули или единицы. Признак равенства разрядов:
Признак неравенства разрядов:
Признак равенства слов:
Устройство контроля четности
Операция контроля четности двоичных чисел позволяет повысить надежность передачи и обработки информации. Ее сущность заключается в суммировании по модулю 2 всех разрядов с целью выяснения четности числа, что позволяет выявить наиболее вероятную ошибку в одном из разрядов двоичной последовательности. Например, если при передаче кода 1001 произойдет сбой во втором разряде, то на приемном пункте получим код 1101 – такую ошибку определить в общем случае затруднительно. Если же код относится к двоично-десятичному (8-4-2-1), то ошибку легко обнаружить, поскольку полученный код (десятичный эквивалент – число 13) не может в принципе принадлежать к двоично-десятичному.
Обнаружение ошибок путем введения дополнительного бита четности происходит следующим образом. На передающей стороне передаваемый код анализируется и дополняется контрольным битом до четного или нечетного числа единиц в суммарном коде. Соответственно суммарный код называется четным или нечетным. В случае нечетного кода дополнительный бит формируется таким образом, чтобы сумма всех единиц в передаваемом коде, включая контрольный бит, была нечетной. При контроле четности все, естественно, наоборот. Например, в числе 0111 число единиц нечетно. Поэтому при контроле нечетности дополнительный бит должен быть нулем, а при контроле четности – единицей. На практике чаще всего используется контроль нечетности, поскольку он позволяет фиксировать полное пропадание информации (случай нулевого кода во всех информационных разрядах). На приемной стороне производится проверка кода четности. Если он правильный, то прием разрешается, в противном случае включается сигнализация ошибки или посылается передатчику запрос на повторную передачу.
Схема формирования бита четности для четырехразрядного кода содержит четыре элемента Исключающее ИЛИ, выполняющий функции сумматоров по модулю 2 (без переноса) и состоит из трех ступеней. На первой ступени попарно суммируются все биты исходного кода на входах А, В, С, D. На второй ступени анализируются сигналы первой ступени и устанавливается четность или нечетность суммы входного кода. На третьей ступени полученный результат сравнивается с контрольным сигналом на входе Е, задающим вид используемого контроля, в результате чего на выходе F формируется пятый дополнительный бит, четности, сопровождающий информационный сигнал в канале передачи.
Арифметические сумматоры являются составной частью так называемых арифметико-логических устройств (АЛУ) микропроцессоров (МП). Они используются также для формирования физического адреса ячеек памяти в МП с сегментной организацией памяти. Сумматоры выполняют арифметическое (в противоположность логическому) сложение и вычитание чисел. Имеют самостоятельное значение и являются также ядром схем арифметико-логических устройств (АЛУ), реализующих разнообразных операций и являющихся непременной частью всех процессоров. Аппаратная сложность и быстродействие сумматора являются очень важными параметрами и поэтому разработано множество вариантов сумматоров, которые имеют разветвленную классификацию. Выделяя главные варианты, остановимся на следующих типах сумматоров:
одноразрядный сумматор;
сумматор для последовательных операндов;
сумматор для параллельных операндов с последовательным переносом;
сумматор для параллельных операндов с параллельным переносом;
сумматор групповой структуры с цепным переносом;
сумматор групповой структуры с параллельным межгрупповым переносом;
сумматор с условным переносом;
накапливающий сумматор.
Наряду с сумматорами могут быть реализованы вычитатели, однако это почти никогда не делается, поскольку вычитание выполняется через сложение с применением дополнительных либо обратных кодов.