3 Практическая работа № 3. Синтез комбинационных схем с множеством выходов. Схема дешифратора для семисегментного индикатора

3.1 Цель занятия

Изучить способы построения комбинационных схем с множеством выходов в заданном базисе элементов (И, ИЛИ, НЕ; И-НЕ; ИЛИ-НЕ).

3.2 Общие сведения

Рассматривается задача реализации системы ПФ (логического функционала)

y₁ = f ₁ (x₁, x₂ , … , x_n ),

y₂ = f ₂ (x₁, x₂ , … , x_n ),

……………………….

y_m = f _m (x₁, x₂ , … , x_n ),

то есть построения схемы, имеющей n входов x₁, x₂ , … , x_n и m выходов y₁, y₂ , … , y_m , функционирующей в соответствии с системой ПФ f₁, f₂, …,f _m. При подаче на входы комбинации значений x₁, x₂ , … , x_n , соответствующей входному набору ПФ, схема формирует на выходах комбинацию значений сигналов y₁, y₂ , … , y_m, соответствующую значениям ПФ на этом наборе.

Задача реализации системы ПФ отличается от задачи синтеза m схем с n входами и одним выходом тем, что при решении необходимо исключить дублирование в m схемах синтезируемых функций. Исключение дублирования обеспечивается при выполнении совместной минимизации ПФ, входящих в систему. При совместной минимизации требуется найти минимальное покрытие не для каждой ПФ в отдельности, а для всех ПФ системы. Таким образом, критериями оптимальности совместной минимизации являются минимальное число различных термов (конъюнкций или дизъюнкций), используемых для покрытия всех функций системы и минимум рангов этих термов. При этом один и тот же терм может входить в покрытие нескольких функций.

Пример 1 - На рисунке 2.1 приведены карты Карно системы ПФ y1, y2, y3, на которых отмечено её минимальное покрытие из четырех склеек. Следует отметить, что ДНФ функций y1 и y3 не являются минимальными

y1 =x1  x3  x4 +x1  x3 x4 +x1  x2 ,

y2 = x1  x2 x3 +x1  x3  x4 ,

y3 =x1  x2 x3 +x1  x2 +x1  x3 x4.

Полученная КС приведена на рисунке 2.2. При ее формировании использована линия групповой связи, которая обозначает множество электрических линий связи. Входы и выходы каждой из этих связей обозначены одинаковыми именами.

y1: y2: y3:

x1 x2 x1 x2 x1 x2

x3x4	00	01	11	10	x3 x4	00	01	11	10	x3 x4	00	01	11	10
00	0	1	0	0	00	0	0	1	0	00	0	1	1	0
01	0	1	0	0	01	0	0	1	0	01	0	1	1	0
11	1	1	0	0	11	1	1	0	0	11	0	1	0	0
10	1	1	0	0	10	0	0	0	0	10	1	1	0	0

Рисунок 3.1

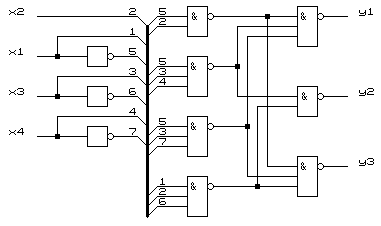
Рисунок 3.2

Пример 2 - Синтезировать в базисе И-НЕ схему дешифратора для управления семисегментным индикатором, работающую согласно таблицы 3.1. При поступлении на вход дешифратора соответствующей комбинации сигналов x1, x2, x3 индикатор должен высвечивать цифры 1, 2, 5, 7.

Наборы входных переменных, отмеченные знаком *, на вход дешифратора не подаются и, следовательно, система ПФ будет не полностью определенной. Расположение сегментов индикатора показано на рисунке 3.3.

Считая, что излучать будет тот сегмент, на который подана логическая единица, составим систему из семи ПФ, каждая из которых определяет работу одного из сегментов индикатора. Например, чтобы на индикаторе высветилась цифра 5, необходимо подать 1 на сегменты a, f, g, c, d, то есть

a = f = g = c = d = 1, b = e = 0.

Таблица истинности системы ПФ представлена в таблице 3.2.

Таблица 3.1
	x1	x2	x3	Инд.
	0	0	0	*
	0	0	1	1
	0	1	0	2
	0	1	1	*
	1	0	0	*
	1	0	1	5
	1	1	0	*
	1	1	1	7

Р
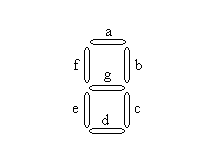
исунок 3.3 - Расположение

сегментов индикатора

Таблица 3.2
x1	x2	x3	Инд.	a	b	c	d	e	f	g
0	0	0	*	*	*	*	*	*	*	*
0	0	1	1	0	1	1	0	0	0	0
0	1	0	2	1	1	0	1	1	0	1
0	1	1	*	*	*	*	*	*	*	*
1	0	0	*	*	*	*	*	*	*	*
1	0	1	5	1	0	1	1	0	1	1
1	1	0	*	*	*	*	*	*	*	*
1	1	1	7	1	1	1	0	0	0	0

Доопределив полученные функции и минимизировав их, получим следующие соотношения:

a = x1 + x2 ; b = + x2 ; c = x3 ;

d = x1 + ; e = ; f = x1 ; g = x1 + .

Воспользовавшись правилом де-Моргана переведем полученные ПФ в базис И-НЕ:

a = ; b = ; c = x3 ;

d = ; e = ; f = x1 ; g = .

Анализируя эти ПФ видим, что b =f , d = g , b участвует в образовании функций d и g:

d = g = .

Функциональная схема дешифратора для семисегментного индикатора, построенная по полученным выше соотношениям, приведена на рисунке 2.4.

Рисунок 3.4

Шифраторы (кодеры) используются чаще всего для преобразования десятичных чисел в двоичный или двоично-десятичный код, например, в микрокалькуляторах, в которых нажатие десятичной клавиши соответствует генерации соответствующего двоичного кода. Поскольку возможно нажатие сразу нескольких клавиш, в шифраторах используется принцип приоритета старшего разряда.

Дешифратор (декодер) – устройство с несколькими входами и выходами, у которого определенным комбинациям входных сигналов соответствует активное со стояние одного из выходов, т.е. дешифратор является обращенным по входам демультиплексором, у которого адресные входы стали информационными, а бывший информационный вход стал входом разрешения. Поэтому часто дешифраторы называют дешифраторами-демультиплексорами и наоборот.

Дешифраторы и демультиплексоры в виде серийных ИМС средней степени интеграции широко используются в информационно-измерительной технике и микропроцессорных системах управления, в частности, в качестве коммутаторов распределителей информационных сигналов и синхроимпульсов, для демультиплексирования данных и адресной логики в запоминающих устройствах, а также для преобразования двоично-десятичного кода в десятичный с целью управления индикаторными и печатающими устройствами.

Дешифраторы как самостоятельные изделия электронной техники имеют 4, 8 или 16 выходов. Если требуется большее число выходов, дешифраторы наращиваются в систему.