В результате минимизации получим мднф для пф и ее инверсии

y =x1 x2 x4 + x1  x2 x4 +x3 ,

y = x3  x4 + x1  x2  x3 + x1 x2  x3 ,

а также МКНФ для ПФ и ее инверсии

y = (x3 +x4 )  (x1 +x2 +x3 )  (x1 + x2 +x3 ) ,

y = (x1 + x2 + x4 )  (x1 +x2 + x4 )  x3 ,

Любая из этих форм ПФ может быть использована для построения КС в базисе Буля (элементов И, ИЛИ, НЕ). Из сравнения этих форм следует, что минимальное число ЛЭ требуется для реализации МКНФ инверсии ПФ. Результат синтеза приведен на рисунке 1.2. Минимальная задержка будет у КС, реализующих прямые формы ПФ, так как для их реализации не требуется дополнительный инвертор для инвертирования функции. На рисунке 1.3 приведен результат синтеза для МДНФ функции.

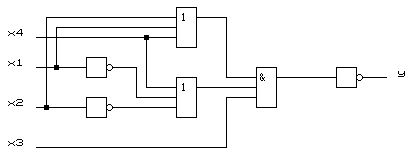
Рисунок 1.2

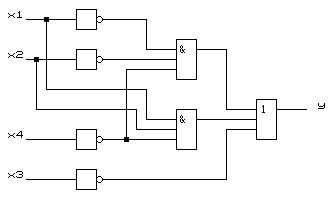
Рисунок 1.3

Для реализации ПФ в базисе И-НЕ используют МДНФ. Выполняют ее двойную инверсии и преобразование Де-Моргана

y =x1 x2 x4  x1  x2 x4  x3 ,

В дальнейшем будем считать инвертор эквивалентным одновходовым элементам И-НЕ, ИЛИ-НЕ. Тогда КС в базисе И-НЕ будет содержать три инвертора, три элемента 3И-НЕ. Схема представлена на рисунке 1.4.

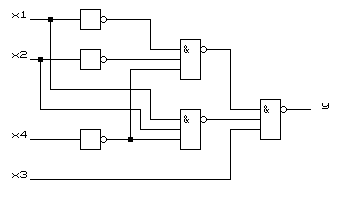
Рисунок 1.4

Для реализации ПФ в базисе ИЛИ-НЕ используют МКНФ. Выполняют ее двойную инверсии и преобразование Де-Моргана. В данном примере более простая реализация будет для преобразованной МДНФ инверсии ПФ

y = x1 + x2 + x4 + x1 +x2 + x4 +x3 ,

КС в базисе ИЛИ-НЕ будет содержать три инвертора, три элемента 3ИЛИ-НЕ. Схема представлена на рисунке 1.5.

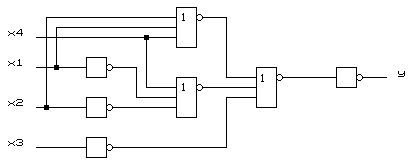
Рисунок 1.5

Если имеются ограничения на число входов ЛЭ и ранг конъюнкции (дизъюнкции) больше допустимого числа входов ЛЭ, то обычно выполняют дополнительные преобразования ПФ, например, факторизацию. Реализуем ПФ на элементах 2И-НЕ

y =x1 x2 x4 + x1  x2 x4 +x3 = (x1 x2 + x1  x2 ) x4 +x3 =

x1 x2  x1  x2 x4  x3 .

Схема представлена на рисунке 1.6.

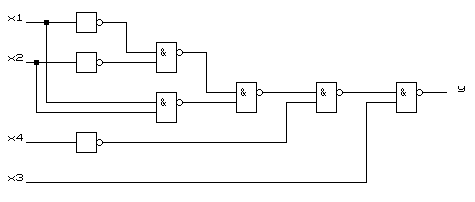
Рисунок 1.6

Оценки сложности и быстродействия КС для рассмотренных вариантов реализации ПФ приведены в таблице 1.1.

Таблица 1.1

Показатель	Вариант реализации
	Рисунок 2	Рисунок 3	Рисунок 4	Рисунок 5	Рисунок 6
Число элементов	6	7	6	7	8
Критерий Квайна	12	13	12	13	13
Относит. задержка	4	3	3	4	5

1.3 Задание

1.3.1 Составить карту Карно в соответствии с заданной функцией по указанному варианту (таблица 1.2).

1.3.2 Провести минимизацию функции. Записать СДНФ и СКНФ после исключения повторяющихся членов.

1.3.3 Разработать электрические схемы в базисах логических элементов:

1) И, ИЛИ, НЕ;

2) И-НЕ;

3) ИЛИ-НЕ.

1.3.4 Выполнить сравнительный анализ полученных схем по сложности и быстродействию.