От кривой рассеяния – к набору структур

Поскольку невозможно однозначно восстановить структуру частицы по данным малоуглового рассеяния, возникает необходимость в решении обратной задачи рассеяния . Из-за потери фазовой информации и усреднения по всем ориентациям, не существует «обратной» формулы Дебая, и, в принципе, очень большое количество структур может быть совместимым с эмпирической кривой рассеяния. В настоящее время разрабатываются различные методы, которые успешно уменьшают неточности и позволяют рассчитывать группы структур и даже структуры низкого разрешения по измеренным кривым рассеяния. Подгонка выполняется, путем измерения собственно I(Q), либо по преобразованию Фурье для функции p(r ). Экспериментальными инвариантами данного метода, с которыми модельная структура должна согласовываться, являются , , D_макс, V и S.

Сферические гармоники

Метод сферических гармоник, развитый в работах X. Штурмана и Д. Свергуна, позволяет определять ab inicio форму молекулы по данным малоуглового рассеяния, используя разложение на сферические гармоники постепенно возрастающего порядка. Для наилучшего сближения рассчитанной структуры и полученной кривой рассеяния применяется метод нелинейной минимизации. Он хорошо работает с однородными частицами приблизительно шарообразными формами, что позволяет получить достаточное приближение при небольшом количестве сферических гармоник. Однако для частиц более сложной формы с «разорванными» поверхностями, метод далек от идеала. На рис. E2.10 в качестве демонстрации возможностей метода сферических гармоник показано восстановление формы димера декарбоксилазы. Существует вариант и для двухкомпонентных частиц (Рис. Е. 2.10 б). Очевидно, что восстановление их формы, требует измерения кривых частицы при разных контрастах.

Рис. Е2.10. (а) Форма димера пируват декарбоксилазы с разрешением L = 4. (А) Вид на молекулу вдоль z-оси. (б) модель (a) повернута на 90^о вокруг х-оси. (в и г) Модель (б) повернута на 45^о и -45^о вокруг Y-оси, соответственно (Кonig et al., 1993). Форма 50S субчастицы рибосом E. coli в двух проекциях. Серым цветом показана форма рибосомной РНК (Serdyuk et al. 1994).

Метод Монте Карло и поиск глобального минимума

Метод Монте-Карло (методы Монте-Карло) − общее название группы численных методов, основанных на получении большого числа реализаций случайного процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи.

Метод поиска глобального минимума, известен под названием simulated annealing, или метод «иммитации отжига». Он базируется на аналогии с физическим процессом кристаллизации металла при постепенном переходе из жидкой фазы в твердую, в результате чего достигается глобальный минимум энергетического состояния.

Методы Монте Карло и поиска глобального минимума были предложены несколькими авторами для первоначального определения структуры с низким разрешением по данным малоуглового рассеяния. Они основаны на более или менее случайных поисках предопределенного конфигурационного пространства для структур, параметры которых наилучшим образом совпадают с данными, не требуют корректировки или минимизации энергетической функции, а главное, длительных расчетов кривых рассеяния по многочисленным моделям. По одному из этих методов в качестве начальной структуры выбирается сфера диаметром, равным максимальному размеру частицы, рассчитанному по кривой рассеяния при помощи функции p(r), и заполненная намного меньшими сферическими модельными атомами. Несложно рассчитать кривую рассеяния, соответствующую модели, и сравнить ее с эмпирической кривой.

К модели можно применить другие ограничивающие условия (выраженные, допустим, как «потери» энергетической функции), например в отношении её компактности или непрерывности занимаемого объема, без разобщенных частей. Метод подыскивает такую конфигурация искусственной модели атома, которая минимизирует функцию, выражающую расхождение между расчетными и эмпирическими кривыми рассеяния.

Генетические алгоритмы

150 лет назад Чарльз Дарвин не мог даже предположить, что математики будут использовать теорию эволюции для вычисления моделей, наиболее подходящих для описания их экспериментальных кривых рассеяния. Дарвиновские термины, используемые ниже, отражают основные этапы создания "лучшей" модели, описывающей экспериментальную кривую рассеяния. Так, термин «хромосома» отражает тот факт, что разработка генетического алгоритма начинается с конструирования двоичной хромосомы, для которой традиционно используются двоичные строки единичной длины. В нашем случае исходные модели создаются при помощи сферических шариков, размещаемых вразброс на решётке, их радиус выбирается меньшим по сравнению с разрешением эксперимента. Решётка представляет ограниченное исследуемое пространство, которое разумно сопоставимо с доступной информацией о максимальных размерах, объёме и радиусе инерции частицы. Обычно набор исходной модели состоит из нескольких сотен структур, называемых «хромосомами», полученных заполнением исследуемого пространства различным количеством шариков. Сконструировав хромосомы мы дальше применяем к ним эволюционный признак выживания сильнейших, позволяя лучшим экземплярам жить, a плохие обрекая на гибель. Традиция разработки генетических алгоритмов предписывает выбирать каждое последующее поколение путем стохастической, но целенаправленной селекции.

После этапа "оценки и соответствия" популяции позволено "воспроизводиться". Часть хромосом, которая обеспечивает кривые рассеяния, наилучшим образом соответствующие данным, сохраняется, чтобы влиться в следующее поколение (обычно это 50% из общей популяции), в то время как остальные удаляются, освобождая место для новых. Применяя два генетических оператора к произвольно выбранным хромосомам в "наиболее соответствующем" наборе, создают новый набор популяции.

Оператор "перехода" обменивается информацией в двух исходных хромосомах согласно предопределённым правилам для получения двух потомков. A оператор "мутации" создаёт новые хромосомы посредством копирования членов "наиболее соответствующего" набора с определённой (маленькой) погрешностью. Затем этап "оценки и соответствия" применяется к следующей популяции, и цикл повторяется до тех пор, пока не достигается "максимальное соответствие", то есть популяция больше не улучшается.

Генетический метод был оттестирован на белках разной формы (βb2-кристаллин, γ-кристаллин, ингибитор рибонуклеазы, лизоцим), структуры которых известны из кристаллографических данных, а кривые рассеяния в интервале Q (0.001- 0.06 Ǻ^-1) были рассчитаны по формуле Е2.27, используя координаты атомов. Рис. Е2.11 демонстрирует действенность генетического алгоритма на двух белках, форма которых далека от сферы.

Число шариков в построенных моделях составляет несколько сотен.

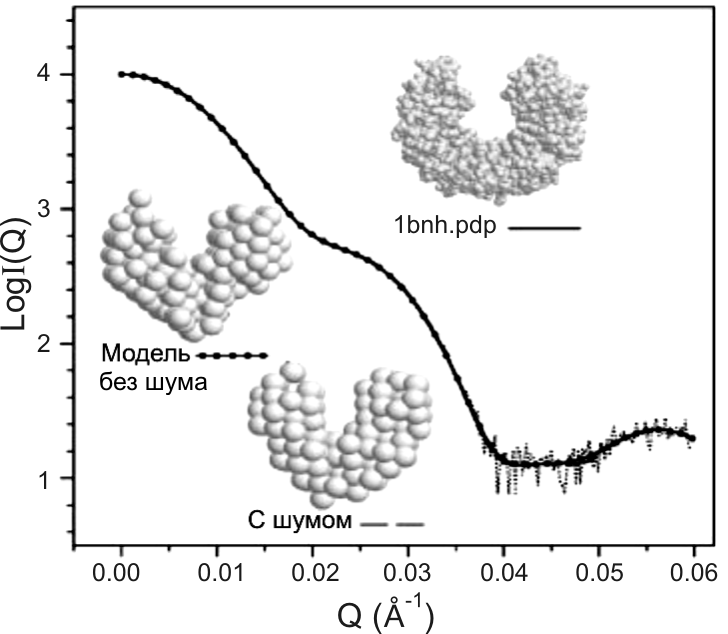
Рис. Е.2.11. Вычисленная по координатам атомов кривая рассеяния в интервале Q (0.001- 0.06 Ǻ^-1) и выведенная модель без наложения и с наложенным шумом для двух белков: βb2-кристаллин (белок состоит из двух глобул, соединенных перемычкой) и ингибитора рибонуклеазы (форма белка напоминает подкову). Атомы водорода и молекулы воды в расчет не принимались (Chacоn P. et al, 1998)

Подытоживая сказанное, заметим, что генетический алгоритм есть не что иное, как оптимизационная процедура, шаги которой описываются с помощью Дарвиновских терминов эволюции. В отличие от других параметрических подходов этот метод извлекает максимальное информационное содержание из кривой рассеяния.