От структуры – к кривой рассеяния

Кривая рентгеновского или нейтронного излучения известных структур элементарных частиц может быть точно рассчитана при помощи формулы Дебая в ее суммарном или интегральном виде (уравнение Е2.3).

Два точечных и два сферических атома

Двухатомная модель представляет особенный интерес для метода триангуляции меченых атомов, в котором сложная частица «упрощается» при помощи контрастной метки. На рис. Е2.7 вы видите две кривые рассеяния – двух точечных и двух сферических атомов, разнесенных на расстояние r₁₂. Первая кривая рассчитана по формуле Дебая, а вторая – с помощью преобразования Фурье. В реальном пространстве структура из двух сферических атомов может рассматриваться как конволюция двух дельта функций со сферой. Амплитуда рассеяния (в обратном пространстве) структуры дается в виде результата соответствующих преобразований Фурье.

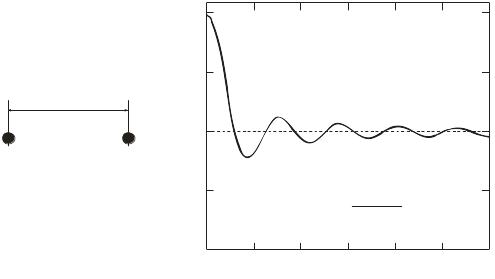
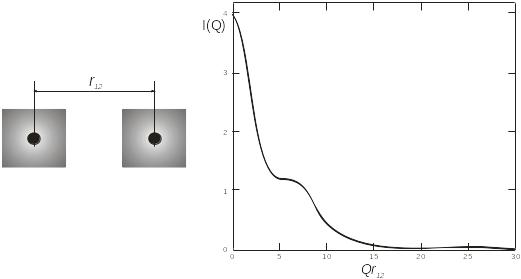
Рис. Е2.7. (a) Вычисления по формуле Дебая (из уравнения Е.2.3) для двух точечных атомов амплитуды рассеяния молекулы (дельта функции), разнесенных на r₁₂:

(б) Кривая рассеяния двух сферических атомов радиуса a = r₁₂/4, разнесенных на расстояние r₁₂.

Сферы и эллипсоиды

Как и в гидродинамике, где коэффициенты трения сначала рассчитываются для простых геометрических форм, первый подход к моделированию кривых рассеяния сводиться к сферам и эллипсоидам. При условии, что сравнение ограничено очень низким разрешением (QR_g ≤ 3), кривая рассеяния любой глобулярной частицы может с успехом аппроксимироваться эллипсоидом вращения с заданной степенью вытянутости. Сферическая частица − предельный случай, представляющий особый интерес. Её уникальность состоит в том, что внутренняя структура такой частицы выражается через распределение плотности рассеяния как функция радиуса, ρ(r), и прямо соответствует среднему вращательному значению. По той же причине сфера является единственной формой, чью амплитуду рассеяния F(Q) можно непосредственно рассчитать из квадратного корня интенсивности рассеяния I(Q). Она соответствует преобразованию Фурье для сферического распределения, а оно способно выражаться в аналитической форме. Пример гомогенной сферы приводится на рис. Е2.8, однако к любому сферическому распределению, включая, например, полые сферы, можно успешно применять метод преобразований Фурье для получения радиальной плотности рассеяния, чтобы определить внутреннюю структуру сферических вирусов при низком разрешении. В диапазоне больших значений QR_g, где появляется первый дополнительный максимум, информационное содержание выше и требуются более сложные формы для успешного моделирования кривой (см. например рис. Е2.4). Но имеются табличные значения I(Q) для сплюснутых и вытянутых эллипсоидов с различными коэффициентами эллипсности, а также для множества других геометрических тел.

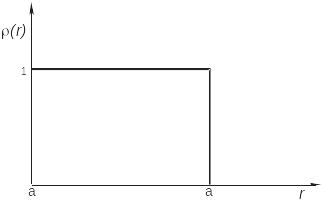
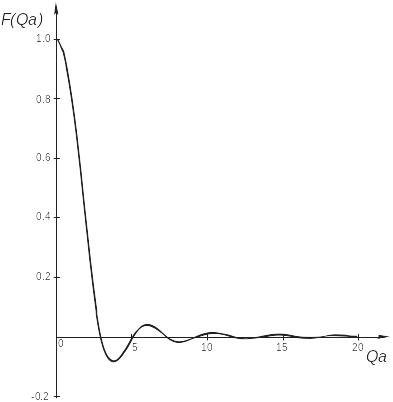
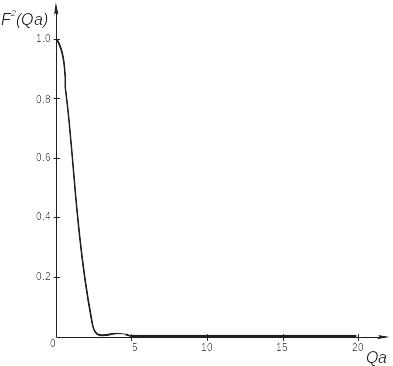
Рис. Е2.8 (a) Распределение границы рассеивающей плотности, ρ(r); (б) амплитуда рассеяния, F(Qa) и (в) интенсивность рассеяния, [F(Qa)]² гомогенной сферы радиуса a. Соответствующими формулами являются

где V – объем сферы, принятый равным 1

Сферы и эллипсоиды

Особый случай представляют собой сферические частицы, для которых (при низком разрешении) усредненная сферическая структура эквивалентна самой структуре. Для них, как в случае сферических вирусов, наиболее эффективен подход, основанный на использовании вариации плотности в малоугловом рассеянии нейтронов ((Jacrot et al., 1977). Основываясь на том факте, что для любой ориентации эллипсоида на пути луча, его проекция равна проекции сферы, были рассчитаны аналитические интегралы для функций рассеяния эллипсоидов. Тогда интенсивность равна сумме интенсивностей от сфер различных радиусов. Результатом является сглаживание второстепенных сферических максимумов. Формулы и таблицы функций интенсивности рассеяния трехосных эллипсоидов даны Мителлбахом и Породом (Mitellbach and Porod, 1962)

Стержни и пластинки

Рассеяние под малыми углами от двух предельных типов асимметричных частиц представляют особый интерес для структурной биологии из-за возможности применения к ДНК и нитевидным комплексам (таким как, например, определенные вирусы), с одной стороны, и мембран с другой. Существуют частицы, у которых один из размеров намного превышает (в десять раз) другой (стержни), и наоборот − один из размеров намного меньше (в десять раз), чем другие два (пластинки). Интуитивно нетрудно догадаться, что флуктуации больших размеров влияют на кривую рассеяния в очень малых областях Q и наоборот. Когда один размер намного превышает другой, соответствующие области Q четко разделены. Можно применить это соображение к формуле Дебая и извлечь выражения для интенсивности рассеяния для очень длинных и очень плоских частиц, которые эквивалентны аппроксимации Гинье для глобулярных частиц.

Расчет по координатам атомов

Кривая рассеяния однозначно вычисляется по известным атомным координатам макромолекулярной структуры в вакууме прямым применением формулы Дебая. Однако в растворе объем v_j должен приписываться каждому атому для расчета контрастной амплитуды каждого атома, m_j = f_j −ρ_{o j}, и отвечать за влияние растворителя. Разработаны специальные программы для таких вычислений. Из-за того, что нейтронная плотность амплитуд рассеяния ρ_o H₂O мала и отрицательна, расчет не очень чувствителен к объемным условиям (m_j = f_j − ρ_oj ) и кривая рассеяния нейтронов в H₂O может считаться разумным приближением к кривой в вакууме.

Для расчета нейтронного рассеяния по атомным координатам можно воспользоваться, например, программой CRYSOL. Но для кривых нейтронного рассеяния нужно знать позиции атомов водорода, которые обычно не включаются в файлы атомных координат, и их необходимо вводить в структуру, используя стереохимические аргументы. Далее программа оценивает выражение:

(Е2.27)

где A_a(Q) – амплитуда рассеяния частицы в вакууме, рассчитанная по атомным позициям, A_s(Q) – амплитуда рассеяния исключенного растворителем объема и A_b(Q) – амплитуда рассеяния гидратационного слоя вокруг частицы. Усреднение проводится по всем ориентациям частицы. A_a(Q) рассчитывается по атомным форм-факторам и позициям. Амплитуда A_s(Q) оценивается по размещению Гауссовых сфер (модельные атомы) в позиции атомов, a граница частицы представляется путем соединения центра масс частицы с самым дальним атомом в каждом направлении. Гидратационная оболочка моделируется толщиной и положением, соответствующим одному слою воды. Исключенный объем частицы и плотность рассеяния гидратационной оболочки нельзя точно определить из кристаллической структуры. При наличии эмпирических данных эти два параметра могут варьироваться для минимизации расхождений между эмпирической и расчетной кривыми рассеяния.