Полидисперсные растворы

Из двух допущений, описанных выше, сделаем менее строгим то, что раствор является монодисперсным. Теперь будем считать, что раствор содержит частицы, неидентичные друг другу. При этом второе допущение о бесконечном разбавлении оставим в силе (взаимодействие между частицами отсутствует).

Рис. Е2.5. (a) Диаграмма Гинье для полидисперсного раствора частиц приблизительно одинакового размера. (б) Диаграмма Гинье для раствора, содержащего мелкие и крупные частицы. Черные пунктирные линии соединяют точки кривой, состоящей из двух частей. Красная вертикальная пунктирная линия соответствует случаю QR_g = 1 для крупных частиц, a зеленая − вертикальная пунктирная линия соответствует случаю QR_g = 1 для более мелких частиц. В примере углы наклона линий данных соотносятся друг с другом с коэффициентом, равным 10, так что радиус инерции более мелких частиц в √10 ≈ 3 раза меньше радиуса более крупных частиц. (в) Диаграмма Гинье для раствора, содержащего частицы, плавно изменяющиеся в размере.

Можно выделить два полезных с экспериментальной точки зрения случая. В первом частицы имеют одинаковую амплитуду рассеяния по величине, но противоположную по вкладу в радиус инерции, так что при этом кривая рассеяния в приближении Гинье достаточно хорошо описывается прямой линией в данном диапазоне Q, где QR_g меньше или равно ~1 для всех частиц (рис. Е2.5а). Измеренные значения I(0) и считаем экспериментальными параметрами. Они соответствуют средневзвешенным значениям амплитуд и радиусам инерции частиц в растворе:

(Е2.23)

(Е2.24)

в котором имеются Nn частиц с амплитудой рассеяния _n и радиусом инерции R_gn. Два этих уравнения служат базой для интерпретации очень важных экспериментов МУР для изучения комплексообразования и взаимосвязей частиц при различных условиях.

Во втором полезном экспериментальном случае частицы имеют различные радиусы инерции, и тогда приближение Гинье удовлетворяет каждому, но в разных диапазонах Q. Это создает ломаную линию графика логарифмической зависимости I от Q², если частицы состоят из двух наборов – больших и малых частиц (как при ассоциации в растворе), или кривую линию, когда размер частиц меняется более плавно (Рис. Е2.5(б) и (в)).

Можно предусмотреть эксперименты по рассеянию под малыми углами для изучения каждого набора частиц в отдельности с достаточной степенью приближения, если распределение по размерам таково, что области значений Q для анализа Гинье четко выражены, как на рис. Е2.5(б). С другой стороны, нельзя извлечь практически никакой информации из изогнутой кривой рассеяния, кроме того, что в данном диапазоне размеров раствор является полидисперсным и при задании форм-фактора частиц рассчитать кривую объемного распределения по размерам. В биохимической части эксперимента потребуются определенные усилия для уменьшения полидисперсности.

Взаимодействующие частицы

Теперь мы сохраним в силе первое допущение относительно монодисперсности, но ослабим второе допущение: раствор больше не считается бесконечно разведенным и каждая частица испытывает воздействие других частиц.

Молекулярное скопление частиц

В литре раствора макромолекул молярной массой M г·моль⁻¹ и концентрацией C мг·мл⁻¹ имеются N частиц:

N = N_AC/M

где N_A – число Авогадро.

Оценим среднее расстояние d между ними, допуская, что они распределены по сетке куба со стороной 10 см:

d = [(10 × 10⁸)/N]^1/3Å

В качестве примера вычислим эти значения для гемоглобина в эритроцитах. Концентрация белка составляет около 300 г ·л⁻¹,^, в общем случае, значение аналогично концентрации в клеточной цитоплазме. Молярная масса гемоглобина − около 64 кДа. Тоgda

Тогда N = 3 × 10²¹

и

d = 66Å

При сферической аппроксимации радиус гемоглобина составляет около 30 Å. Расстояние между частицами в растворе 300 г· л⁻¹ менее 10 Å, что соответствует двум-трем слоям молекул воды

В живой клетке концентрация белков столь высока, что вне организма условия эксперимента по рассеянию под малыми углами были бы очень далеки от бесконечного разведения. Положение и ориентация каждой частицы в концентрированном растворе сильно зависит от других частиц, даже когда отсутствует дальнее взаимодействие между ними, просто хотя бы потому, что вокруг частицы недостаточно места для свободного перемещения или вращения. Для частиц с приблизительно сферической симметрией (при которой все ориентации эквивалентны) влияние высоких концентраций на малоугловую кривую рассеяния можно вычислить с использованием «жидкоподобной» потенциальной функции, при этом межчастичное взаимодействие и упаковка поглощаются молекулами в жидкости. Для ассиметричных частиц задача усложняется многократно, если асимметрия велика (очень длинные или очень плоские частицы), они тогда образуют волокна или пучки.

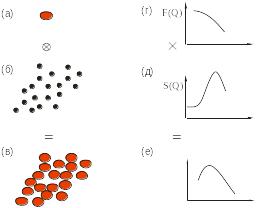
Рис. Е2.6. Слева. (a) Квази-сферическая частица, описываемая некоторым распределением плотности рассеяния. (б) Распределение центров масс частиц (точки) в жидкости. (в) Квази-сферические частицы в жидкости, описываемые как конволюция (a) и (б). (г) Форм-фактор или интенсивность рассеянного излучения частицы в обратном пространстве. (д) «Структурный» фактор жидкости, состоящей из точечных молекул. (е) Интенсивность рассеянного излучения квази-сферическими жидкими молекулами, обусловленная умножением (г) и (д). Напоминаем, что преобразование Фурье для конволюции есть просто умножение (см. Главу A3). Справа. Концентрационная зависимость кривой рассеяния раствора лизоцима при рH 7.0 в 50 мМ Hepes буфере при концентрации от 5 до 200 мг·мл^-1. Кривые рассеяния нормализованы на концентрацию. Резкое уменьшение интенсивности при Q, меньших ≈ 0.02 Å^-1, связано с аппаратурными искажениями (Arai and Hirai, 1999).

Потенциальная функция, описывающая молекулы в жидкости, соответствующее распределение частиц и коэффициент рассеяния (амплитуда волны в обратном пространстве как функция Q) для точечных молекул показаны на рис. Е2.6 (слева). Теперь можно спрогнозировать кривую рассеяния группой частиц со сферической симметрией, которая организована в соответствии с данным межчастичным потенциалом, применяя конволюционно-мультипликационую связь между реальным и обратным пространством. При отталкивающем потенциале коэффициент рассеяния возрастает от Q равного нулю, тогда как форм-фактор обычно уменьшается. В результате кривая рассеяния сглаживается в области аппроксимации Гинье, приводя к кажущимся радиусу инерции и значениям I(0), которые меньше тех, что соответствуют частице в разбавленном растворе. Фактор рассеяния стремится к 1 для больших значений Q, а они не намного больше значений в области аппроксимации Гинье и зависят от близости частиц. Так что эффект от межчастичной интерференции на кривую рассеяния становится ничтожно малым, и высокие макромолекулярные концентрации (если они имеются) могут использоваться для измерения при «высоких» Q. Рис Е2.6 (справа) демонстрирует экспериментальный ход кривой рассеяния для раствора лизоцима в широком интервале концентраций и векторов рассеяния, подтверждающий теоретические прогнозы.