Асимптотическое поведение кривой рассеяния при больших значениях q. Соотношение Порода

В начале 1950-х гг. Пород ввел характеристическую функцию частицы, из которой можно рассчитать асимптотический характер изменения кривой рассеяния при больших значениях Q. При этом необходимо соблюдать условие, которое состоит в том, что частица должна иметь отчетливо выраженную оболочку, за пределами которой находится гомогенный растворитель. Тогда при больших значениях Q, интенсивность I(Q) колеблется вокруг асимптотической линии, соответствующей

(Е2.10)

где S есть площадь наружной поверхности частицы.

При больших значениях Q кривая рассеяния резко падает, как Q⁻⁴. Формально, точное измерение I(Q) в этом диапазоне векторов рассеяния позволяет определить S. На практике, однако, уравнение. Е2.10 редко используется для этой цели. Причина кроется в очень маленькой интенсивности рассеяния частицей (за вычетом растворителя, разумеется) при больших значениях Q (величины на 2-3 порядка, меньше, чем I(0)).

Полная кривая рассеяния. Функция распределения расстояний

Кривая рассеяния измеряется как функция от Q в обратном пространстве. Возникает интересный вопрос: какую информацию содержит она о структуре частицы в реальном пространстве? Напомним, что обратное и реальное пространство математически связаны преобразованием Фурье.

В случае малоуглового рассеяния, при котором I(Q) − это результат вращательного усреднения |F(Q)|², обратное преобразование Фурье I(Q) становится функцией, которая зависит от расстояния r между частями структуры:

(Е2.11)

Эта ситуация похожа на синтез Паттерсона в кристаллографии, который является обратным преобразованием Фурье интенсивности дифрагированной волны. В этом уравнении I(Q) относится к одиночной частице с объемом V. Функция γ (r) является корреляционной функцией, определенной ранее формулой Е2.6 .

Функция Vγ (r) равнозначна радиальной функции Паттерсона. Интеграл от 0 до ∞ в уравнении E2.11 фактически равен интегралу от 0 до D_макс, максимальному расстоянию в частице, поскольку разностная плотность рассеяния равна нулю для r больших, чем D_макс. В случае частицы с однородной плотностью рассеяния (ρ(r) = ρ), мы можем записать:

(Е2.12)

где γ₀(r ) известна как характеристическая функция Порода, которая зависит только от геометрии частицы.

Чтобы избавиться от объема в корреляционной функции, для монодисперсных систем, например, в качестве нормирующего коэффициента естественно выбрать величину :

(E2.13)

Этот же результат появляется в уравнении. E2.12 и в интегральной форме уравнения Дебая (E2.4a), которое сейчас можно записать как преобразование Фурье для Vγ (r):

(Е2.14)

или

(E2.15)

где

(Е2.16)

Функция распределения расстояний

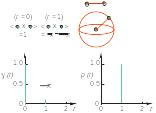
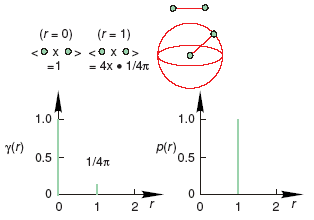
Пусть мы имеем частицу с единичным объемом, состоящим из двух небольших объемов с плотностью рассеяния, равной единице (ρ = 1) и разделенных единичным расстоянием (r = 1). Количество точек, на которые расстояние r удалено от каждого объема, пропорционально площади сферической поверхности 4πr². Применяя уравнение Е2.12 для расчета γ (r), получаем среднее значение произведения величин ρ, разделенных расстоянием 1, равное 1/4π. Здесь же показана соответствующая этому случаю функция p(r) (уравнение. Е2.16). Отметим, что p(r) фактически является функцией распределения расстояний. Её вид говорит нам о том, что в нашем примере существует только одно расстояние со значением 1.

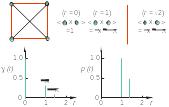
Этот рисунок иллюстрирует те же расчеты, которые были приведены выше, для частицы, состоящей из четырех единичных объемов одинаковой плотности рассеяния. Четыре единичных объема расположены таким образом, что образуют квадрат с единичной стороной. Функция распределения пар расстояний теперь говорит нам, что частица содержит четыре единичных расстояния (стороны квадрата) и два расстояния, умноженные на √2 (диагонали).

Эти примеры наталкивают на мысль, что функция p(r) однозначно определяет структуру и последнюю можно вывести из неё. В принципе так и есть. Действительно если частица содержит всего несколько атомов, то вывести её строения из функции межатомных расстояний не составляет труда. Однако для многоатомных молекул возникает почти непреодолимое препятствие: практическое осуществление такой возможности для сложных молекул упирается в следующую трудность: чем сложнее молекула, чем больше в ней атомов, тем больше вероятность слияния в общие пики функции p(r) различных межатомных векторов

Функция p(r) называется функцией распределения пар расстояний частицы. Она представляет численное распределений "расстояний", соединяющих пары элементов объема в частице, взвешенное по их плотности рассеяния.

Функция распределения пар расстояний является обратным преобразованием Фурье для I(Q) (комбинация уравнений Е2.11 и Е2.16).

(Е2.17)

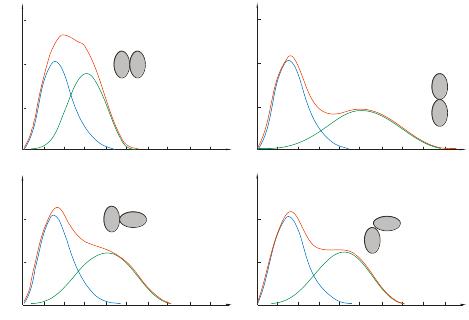
Рис. Е2.4. (a) Интенсивности рассеяния и функции распределения пар расстояний для сферы (черный), сплюснутого (зеленый) и вытянутого эллипсоида вращения (синий) одного и того же объема.(б) Функции распределения пар расстояний димеров. Синяя линия – функция мономера. Красная – димера, а зеленая – разность между ними (по О. Глаттеру) (Glatter and Kratky, 1982)

Таким образом, при условии, что кривая рассеяния известна в интервале векторов от нуля до бесконечности, можно рассчитать функцию p(r) частицы.

Измерение I(Q) при Q = 0 является, конечно же, невозможным, как также невозможно измерить кривую рассеяния при бесконечно больших Q. Интеграл поддается вычислению, если мы заполним отсутствующие части кривой путем экстраполяции в контексте одиночной частицы. Например, кривую можно проэкстраполировать до Q = 0, использовав аппроксимацию Гинье, и до Q→∞ при больших значениях Q, использовав соотношение Порода. Функции распределения пар расстояний для частиц различной формы показаны на рис. Е2.4.