Электрофоретическое рассеяние света

Рассеяние света от движущихся частиц получило название частотного эффекта Доплера.

По аналогии со звуковой волной, сдвиг Доплера на оптической частоте света равен:

(31.19),

где ν₀ – исходная частота источника света, взятая в качестве эталона, а c – скорость света для рассеянного света). Если источник света движется под некоторым углом θ по отношению к детектору, то значение сдвига Доплера уменьшается на фактор sin θ:

q u (31.20)

Уравнение 31.20 показывает, что, измеряя ν, можно получить значение скорости частиц u, поскольку значение вектора рассеяния q определяется углом рассеяния света.

Лазерный велосиметр Доплера известен довольно давно. В лазерном велосиметре Доплера падающий свет освещает поток движущихся частиц. На практике, один луч лазера, расщепленный на два равных по интенсивности, фокусируется в одной точке в потоке поля. Интерференционная картинка формируется в точке пересечения лучей и создает измеряемый объем. Частицы, проходя через такой объем, создают вспышки света. Результирующая частота, определяемая фотодетектором, напрямую связана со скоростью частиц.

Электрофоретическое рассеяние света является частным случаем доплеровской велосиметрии. Оно позволяет с измерить электрофоретическую подвижность по сдвигу Доплера рассеянного света. Принципиальным преимуществом этого метода является его способность охарактеризовать электрофоретические свойства многих частиц одновременно. Когда раствор заряженных частиц находится в электрическом поле, то частицы движутся к электродам с противоположной полярностью с определенной скоростью. Эффект электрического поля должен быть включен в уравнение корреляционной функции как дополнительный член, считая, что переориентация частиц и химические реакции отсутствуют.

Рассеяние и флуоресценция в условиях малого числа частиц Рассеяние малым числом частиц

Давайте представим, что мы проводим эксперимент по наблюдению за числом частиц в большом объеме. При большом числе частиц в объеме контролировать их число наиболее просто по флуктуациям, определяемым методом ДРС, поскольку общая интенсивность рассеянного света, регистрируемая детектором, является суммой интенсивности рассеяния от каждой частицы. Изменения интенсивности, обусловленные числом флуктуаций, обычно малы именно в силу большого числа частиц в объеме.

В системах, состоящих из сравнительно небольшого числа частиц, возможны значительные отклонения некоторых физических величин, характеризующих системы, от их средних значений. Такие отклонения называются флуктуациями.

Для этого случая важными являются два вклада во временную зависимость интенсивности рассеяния. Один из них связан с входом и выходом частиц из рассеивающего объема, что вызывает временные флуктуации. Другой связан с диффузией частиц внутри рассеивающего объема на расстояниях порядка длины волны света, которая также вызывает временные флуктуации. Если предположить, что эти два процесса не коррелированы друг с другом, тогда для гомодинного детектирования нормализованную корреляционную функцию можно представить как:

(32.3)

Первый член в правой части этого уравнения связан флуктуацией общего числа частиц внутри рассеивающего объема, а второй обусловлен вкладом диффузии. В уравнении 32.3 N₀ это среднее число частиц в рассеивающем объеме; γ – характерное время, необходимое для диффундирования частицы через рассеивающий объем и которое имеет величину порядка L²/24N₀D_t (где, L характерный размер рассеивающего объема), A и B – константы.

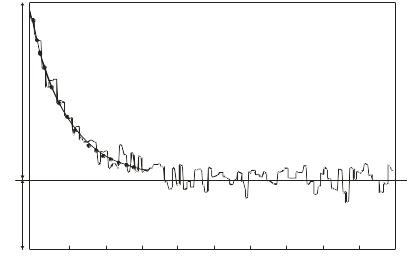
Рис. 32.1. Корреляционная функция времени интенсивности рассеянного света раствором вируса птичьего миелобластоза (M = 4×10⁸ Да, s = 680S, D_t = 0.31×10⁷ см² сек⁻¹) в очень низкой концентрации (2×10⁷ частиц на см³). Рассеивающий объем равен около 10⁻³ см³. Присутствие базовой линии, смещенной по отношению к нулевой коррелятора, является мерой числа флуктуаций, ожидаемых при низких концентрациях (Salmeen et al., 1975)

Очевидно, что при высоких концентрациях второй член в уравнении 32.3 доминирует и по экспериментально наблюдаемой константе спада вычисляется константа диффузии. При очень низких концентрациях, когда, N₀ сравнимо с BN₀², оба компонента вносят вклад в наблюдаемую корреляционную функцию. На рисунке 32.1 представлена корреляционная функция для образца вируса птичьего миелобластоза, в которую уже существенный вклад вносят флуктуации от числа частиц, поскольку в рассеивающем объеме содержится всего около 2000 частиц. Однако собственно рассеяние при такой концентрации и такой молекулярной массе вируса (М = 4×10⁸ Да) является настолько слабым, что точное значение коэффициента диффузии вируса определить не представляется возможным ни из когерентной, ни из некогерентной составляющей.