Флуктуации и временные корреляционные функции

Для того, чтобы получить информацию о динамике флуктуирующих систем, мы должны выбрать один из двух различных, но близких по физическому смыслу подходов. Мы можем анализировать флуктуирующие системы на основе частотных компонентов с разными амплитудами, получая спектр частот флуктуаций со свойствами A, <ΔA²(ν)> , где ν это частота. Однако, имеется другой, более точный метод, в котором измеряется непосредственно временная корреляционная функция флуктуаций <A(t), A(t + τ)>, где τ – корреляционное время, характеризующее флуктуации в системе.

В этой главе мы будем обсуждать только эксперименты с использованием техники временных корреляционных функций, поскольку она обеспечивает более высокую точность по сравнению с техникой спектрального анализа. Иногда, для визуализации результатов мы будем иногда пользоваться спектром частот. Начнем с корреляционных функций.

Корреляционные и кросс-корреляционые функции

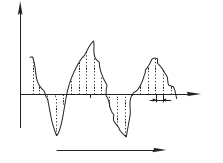
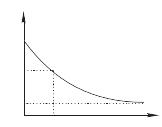
Рис. 31.2. (а) Изображение некого свойства А(t), флуктуирующего во времени относительно своего среднего <A>, равного нулю. Временная ось разбивается на ряд дискретных интервалов Δt. (б) Корреляционная функция <A(0) А(τ)>, oписывающая флуктуационный процесс, изображенный в (а). Начальное значение функции равно <A²>. Для времен значительно больших, чем корреляционное время процесса τ_А, корреляционная функция равна <A>²

Флуктуирующий сигнал A(t), изображенный на рисунке 31.2а, обладает следующими свойствами: свойство А для времени t всегда отлично от свойства А для времени t+Δt. Когда время τ мало по сравнению с типичным временем флуктуаций переменной А(t), A(t + τ) будет близко к величине A(t). Когда величина τ увеличивается, отклонение A(t + τ) от A(t) становится более вероятным. Таким образом, можно сказать, что величина A(t + τ) коррелирует с A(t) когда τ мало, но эта корреляция теряется, когда τ становится большим по сравнению с характерным периодом флуктуаций. Мерой такой корреляции является автокорреляционная функция, определяемая как:

(31.1)

Если ось времени t разбить, как это сделано на рисунке 31.2а на дискретные интервалы Δt, так что t = j Δt, τ = n Δt, T =N Δt, a t+ τ = (j + n)Δt, = Δt, то интегрирование в уравнении Г10.1 можно заменить суммированием:

<A> (31.2а)

(31.2б)

где А_j есть значение свойства в начале j-го интервала.

Мы ввели дискретизацию в описание флуктуационного процесса с тем, чтобы продемонстрировать, как корреляционная функция меняется со временем. Из рисунка 312а видно, что некоторые члены в суммах уравнений 31.2а и 31.2б отрицательны, например А₃ и А₄. Следовательно, в этих суммах часть вкладов будет положительна, а часть отрицательна. С другой стороны величина <A(0) A(t)> всегда положительна, так как А_j²≥ 0, и ожидается большой. Таким образом, мы можем ожидать, что корреляционная функция всегда будет постоянной, равной начальному значению для всего отрезка времен или уменьшаться от максимального значения <A²> до минимального <A>² (рис. 31.2б).

Отметим, что в большинстве практических применений корреляционная функция падает моноэкспоненциально:

(31.3)

где τ_кор есть корреляционное или релаксационное время флуктуирующего сигнала.

Корреляционная функция двух свойств А и B описывается кросс-корреляционными функциями:

(31.4а)

и

(31.4б)

Корреляторы

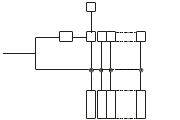
Рис. 31.3. Схема коррелятора для анализа флуктуирующих процессов (см. текст)

В лабораторных условиях превращение флуктуаций сигнала в корреляционную функцию выполняется с помощью прибора, называемого коррелятором (рис. 31.3). Флуктуирующий сигнал в цифровом виде передается по двум каналам: накопительному и общему каналу коррелятора. Накопитель, считает импульсы за определенный промежуток времени, Δt, длительность которого задается тактовыми кристаллическими часами. В конце этого промежутка содержимое переносится в первый регистр коррелятора. Затем коррелятор начинает считать импульсы для второго идентичного временного интервала. Этот процесс продолжается в течение всего эксперимента, так что регистры коррелятора содержат информацию о флуктуирующем сигнале за промежуток времени n , где n число регистров коррелятора, а называется временем выборки или временем сэмплирования, которое выбирается, как правило, в интервале времени от 2 нсек до 1сек. Время выборки должно соответствовать типичным корреляционным временам системы. Очевидно, что для быстрых процессов время выборки, берется малым, a для медленных процессов – большим.

Корреляционные функции поля и интенсивности

Для единичной частицы наведенный диполь p, который является источником рассеяния, определяется падающим полем E и поляризуемостью частицы α:

p = α E (31.5)

Свет, излучаемый всеми индивидуально индуцируемыми диполями, собирается на детекторе, где результирующее электрическое поле зависит от относительной позиции и ориентации всех частиц в рассеивающем объеме. Типичная геометрическая картина рассеяния света представлена на рисунке 31.4. Корреляционная функция рассеивающего электрического поля, G ⁽¹⁾(τ), называемая корреляционной функцией первого порядка, определяется, как:

G⁽¹⁾(τ) = < E(t) E(t +τ) > (31.6)

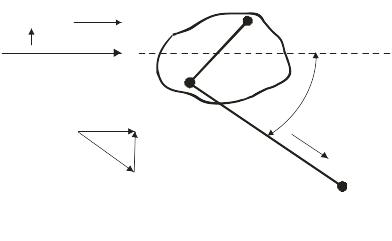
Рис. 31.4. Типичнaя геометрия рассеяния света. E₀ – амплитуда падающего поля; k₀ и k₁ – падающий и рассеивающий волновые векторы; q = k₀ − k₁ –волновой вектор рассеивания, определяемый углом рассеяния θ и длиной волны падающего света λ; n – показатель преломления среды

На практике, в силу квадратичной природы детектирования измеряется корреляционная функция флуктуаций интенсивности. Для интенсивности I, которая пропорциональна квадрату вектора электрического поля <E²>, нормализованная корреляционная функция, G⁽²⁾(τ), называемая корреляционной функцией второго порядка, вычисляется как:

G⁽²⁾(τ) = < I(t) I(t + τ) > (31.7)

Для систем, содержащих большое количество независимых источников рассеяния света, (гауссово приближение) связь между G⁽¹⁾ (τ) и G⁽²⁾ (τ) задается соотношением:

G⁽²⁾(τ) = 1 +│G ⁽¹⁾ (τ)│² (31.8)

Корреляционные функции и частотный спектр флуктуаций

Как было упомянуто выше, частотный спектр I(ν) и корреляционная функция G(τ) полностью эквивалентны при описании динамического поведения равновесных систем, поскольку они связаны фурье-преобразованием:

(31.9)

где ν частота в Гц. Так, если I(ν) имеет форму Лорентца на нулевой частоте, тогда G(τ) имеет форму спадающей экспоненциальной функции с константой времени, равной обратной величине полуширины линии Лорентца. Эти простые функции верны для описания всех элементарных стохастических процессов и применимы для интерпретации поведения большинства систем, которые будут обсуждаться в дальнейшем. Простые примеры связи между корреляционной функцией и частотным спектром приведены на рисунке 31.5.

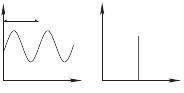
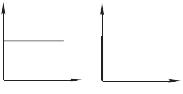
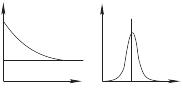
Рис. 31.5. Корреляционные функции и частотный спектр для трех простейших моделей флуктуационных процессов: (a) синусоидальная функция; (б) постоянная; (в) простейший стохастический процесс