4 Решение систем линейных алгебраических уравнений
4.1 Общие сведения
Система линейных
алгебраических уравнений (СЛАУ) с
матрицей вещественных коэффициентов
и вектором свободных членов
относительно неизвестного вектора
записывается в координатной форме
следующим образом:
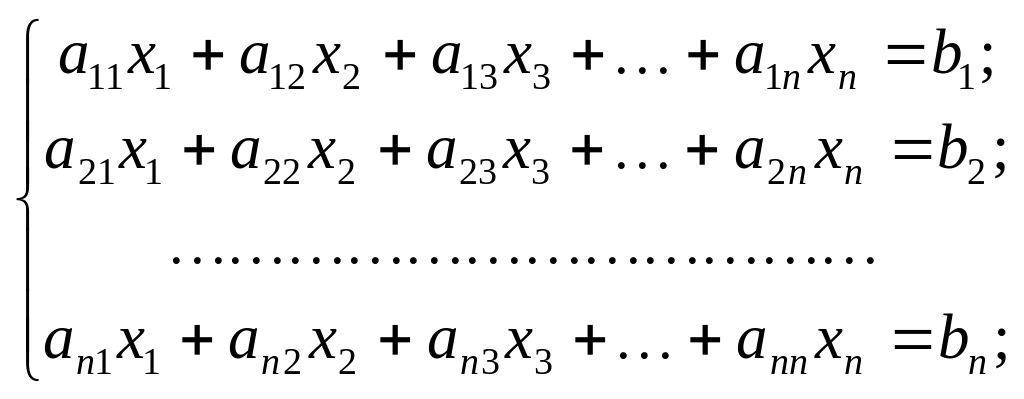, (4.1)
или
(сокращенный вид координатной формы),
или в векторной форме:
.
Каждое уравнение описывает прямую (n = 2), плоскость (n = 3), гиперплоскость (n 4) в вещественном пространстве, поэтому решить систему – значит найти точку х* их пересечения в этом пространстве.
Будем предполагать, что определитель матрицы А отличен от нуля:
,
так что решение существует и единственно.
Методы численного решения СЛАУ делятся на две группы: прямые (точные) и итерационные (приближенные).
В прямых методах решение находится за конечное число арифметических операций (метод Крамера, метод исключений Гаусса). Точными их, конечно, можно назвать, если отвлечься от погрешностей округления (вычислительных погрешностей).
Итерационные методы – это методы последовательного приближения. Решение СЛАУ находится как предел при k последовательных приближений x(k) , где k – номер итерации. Как правило, за конечное число итераций этот предел не достигается. Обычно задается малое число , и вычисления проводятся до тех пор, пока не выполнится оценка
.
Качество разных итерационных процессов сравнивается по необходимому числу итераций k().
4.2 Метод гаусса
Наиболее известным из точных методов решения СЛАУ является метод исключений Гаусса. Он основан на приведении матрицы системы к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы.
Предположим, что a11 0. Разделим первое уравнение (4.1) на a11, получим
Затем из каждого из остальных уравнений вычитается первое уравнение, умноженное на соответствующий коэффициент ai1 (i=2,3,,n).
Эти уравнения принимают вид:
Далее аналогичную процедуру выполняют с этой системой, оставляя в покое первое уравнение. Только теперь делят на a22(1) 0.
В результате исключения неизвестных приходим к СЛАУ с верхней треугольной матрицей с единицами на главной диагонали:
(4.2)
Завершен прямой ход метода Гаусса.
Обратный ход метода Гаусса заключается в нахождении неизвестных xn , xn–1 , ... , x1 , причем именно в таком порядке.
xn уже определено из последнего уравнения системы (4.2), а общая формула обратного хода имеет вид
Таким
образом, для того, чтобы практически
воспользоваться методом Гаусса,
достаточно указать алгоритм, по которому
исходная матрица А преобразуется
к треугольному виду (4.2), и указать
соответствующее преобразование правых
частей системы, то есть указать расчетные
формулы для
и
,
где k=1,2,...,n
– шаг прямого хода Гаусса.
Эти формулы имеют вид
(4.3)
Здесь
Из
этих формул сразу видно основное
ограничение метода – все элементы
,
на которые производится деление, должны
быть отличны от нуля.
Число
называется ведущим элементом на
k-ом шаге исключения.
Даже если это число не нуль, а просто
близко к нулю, в процессе вычислений
может происходить сильное накопление
погрешности.
Чтобы избежать катастрофического влияния вычислительной погрешности, применяют модификацию метода Гаусса – метод Гаусса с выбором главного элемента.
Она заключается в том, что требование неравенства нулю диагональных элементов , на которые происходит деление в процессе исключения, заменяется более жестким: из всех оставшихся в k-ой строке (столбце, матрице) нужно выбрать наибольший по модулю элемент и переставить столбцы или (и) строки так, чтобы этот элемент оказался на месте элемента . Соответственно различают методы Гаусса с выбором главного элемента в строке (в столбце) и метод Гаусса с глобальным выбором главного элемента.
Пример 1. Метод Гаусса с выбором главного элемента в строке.
Перестановка Исключение
Перестановка Исключение
Для сравнения приведем реализацию метода Гаусса с выбором главного элемента в столбце.
Перестановка Исключение
Перестановка Исключение
Реализация прямого хода метода Гаусса требует 2n3/3 арифметических операций, а обратного хода – n2 арифметических операций. Для сравнения: решение СЛАУ по методу Крамера требует n(n+1)!–1 арифметических операций.