Лекція№1
Тема: Вступ. Виникнення та значення математичної логіки.
План.
1. Вступ. Виникнення та значення математичної логіки.
Література:
Гринченков Д.В. Потоцкий С.И. Математическая логика и теория алгоритмов для программистов. М.: Кнорус, 2010. – 208с.
Зміст
1. Вступ. Виникнення та значення математичної логіки
п
Лекція №2
Тема: Алгебра висловлень
План
Поняття висловлення. Види висловлень.
Логічні операції над висловленнями.
Література:
Прийма С.М. Математична логіка і теорія алгоритмів: Навчальний посібник – Мелітополь: ТОВ «Видавничий будинок ММД», 2008. – 134с
Зміст
Поняття висловлення. Види висловлень.
2. Логічні операції над висловленнями
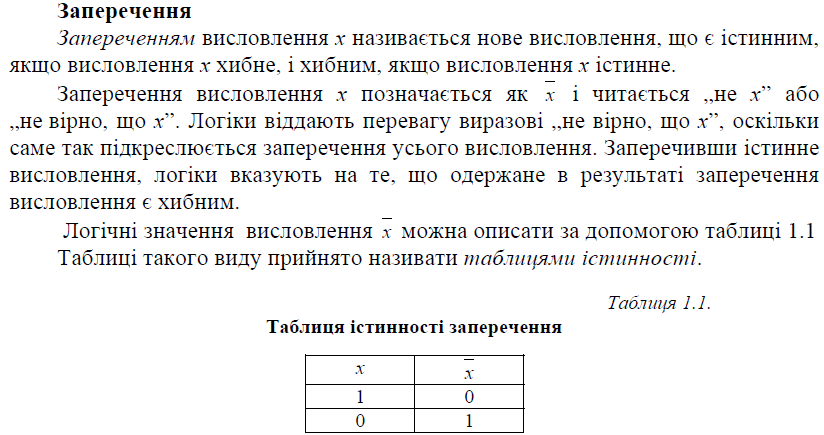
Лекція№2
Тема: Формули алгебри висловлень
План
Формули алгебри висловлень
Обчислення значень формул
Література:
Прийма С.М. Математична логіка і теорія алгоритмів: Навчальний посібник – Мелітополь: ТОВ «Видавничий будинок ММД», 2008. – 134с.
Зміст
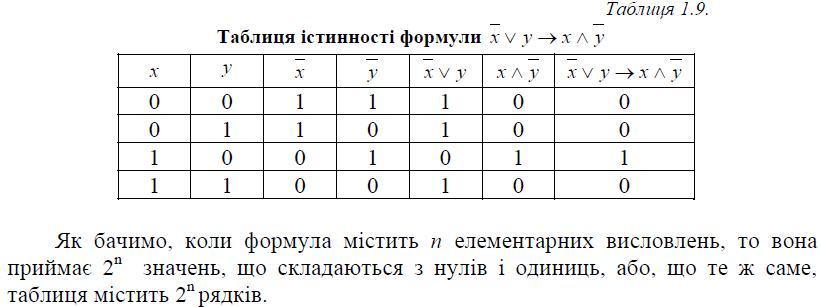
Лекція №4
Тема: Основні тотожності бульової алгебри
План
Закони логічних операцій (основні тотожності)
Література:
Прийма С.М. Математична логіка і теорія алгоритмів: Навчальний посібник – Мелітополь: ТОВ «Видавничий будинок ММД», 2008. – 134с.
Зміст
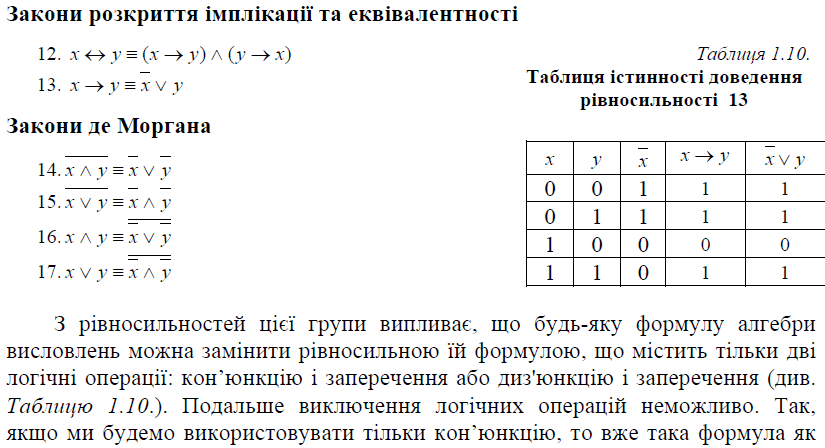
Закони логічних операцій (основні тотожності)
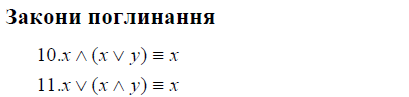
Лекція №5
Тема: Формули в ДДНФ
План
Нормальні форми, досконалі нормальні форми
Алгоритм переходу від довільної формули алгебри висловлень до ДДНФ через побудову таблиці істинності
Алгоритм переходу від довільної формули алгебри висловлень до ДДНФ
Література
Прийма С.М. Математична логіка і теорія алгоритмів: Навчальний посібник – Мелітополь: ТОВ «Видавничий будинок ММД», 2008. – 134с.
Зміст
Нормальні форми, досконалі нормальні форми
2. Алгоритм переходу від довільної формули алгебри висловлень до ДДНФ через побудову таблиці істинності
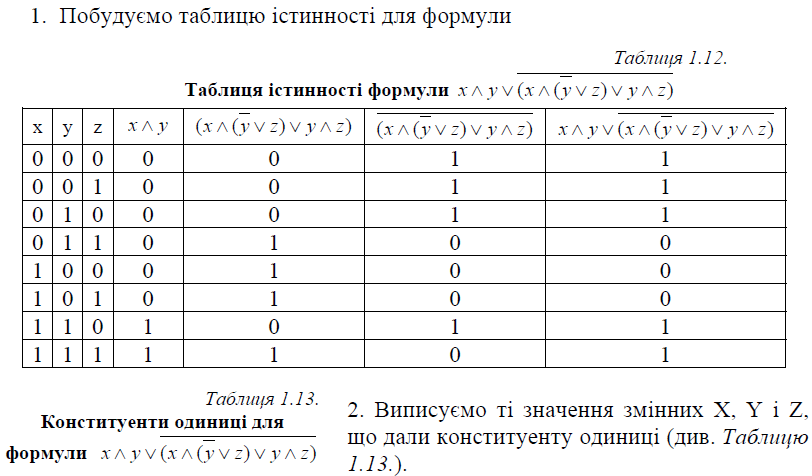
3.Алгоритм переходу від довільної формули алгебри висловлень до ДДНФ
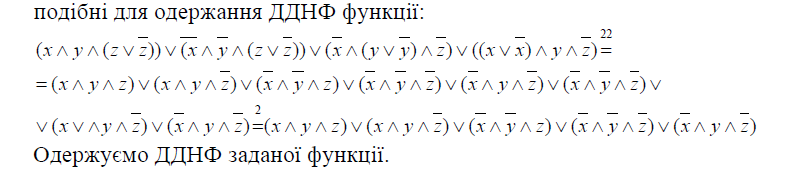
Лекція №6
Тема: Формули в ДКНФ
План
Алгоритм переходу від довільної формули алгебри висловлень до ДКНФ через побудову таблиці істинності
Алгоритм переходу від довільної формули алгебри висловлень до ДКНФ
Література
Прийма С.М. Математична логіка і теорія алгоритмів: Навчальний посібник – Мелітополь: ТОВ «Видавничий будинок ММД», 2008. – 134с.
Зміст
Алгоритм переходу від довільної формули алгебри висловлень до ДКНФ через побудову таблиці істинності
Алгоритм переходу від довільної формули алгебри висловлень до ДКНФ
Лекція №7
Тема: Рівносильні та тотожно істинні формули в бульовій алгебрі
План
Основні визначення
Рівносильні перетворення формул
Література
Прийма С.М. Математична логіка і теорія алгоритмів: Навчальний посібник – Мелітополь: ТОВ «Видавничий будинок ММД», 2008. – 134с.
Зміст
Основні визначення
Рівносильні перетворення формул
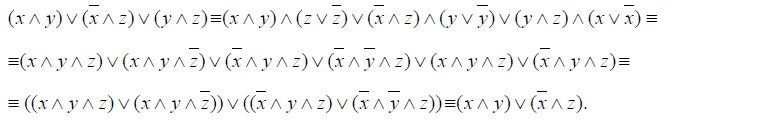
Лекція №8
Тема: Твердження, умови, ознаки, властивості, означення
План
Поняття твердження та умови в математичній логіці
Поняття ознаки, властивості та означення в математичній логіці
Література
Прийма С.М. Математична логіка і теорія алгоритмів: Навчальний посібник – Мелітополь: ТОВ «Видавничий будинок ММД», 2008. – 134с.
Зміст
Поняття твердження та умови в математичній логіці
Твердження — декларативне речення, що може бути істинним або хибним. Твердження не тотожнє реченню, воно радше визначає ідею, яка покладена в реченні. Одне й те ж саме твердження може бути виражене різними реченнями. У формальній логіці строго сформульовані твердження називають предикатами.
Предика́т — одне із фундаментальних понять логіки, а також математичної логіки, умова сформульована в термінах деякої точної логіко-математичної або неформальної мови.
Предикат містить позначення для довільних об'єктів певного класу (змінні). При заміщенні змінних іменами об'єктів даного класу, предикат задає точно визначене висловлювання.
Прикладами предикатів можуть бути вирази (x > 2), (x+3) = y, (x > 3 та y < x). При заміщенні x на 2 та y на 5 другий із предикатів визначає істинне висловлення, а інші два — хибні.
Можливі і інші варіанти визначення предиката. Так, іноді роблять природнє ототожнення, вважаючи, що сімейство рівносильних умов задає один і той самий предикат. Висловлювання можна розглядати як окремий випадок предикатів з «фіктивними» змінними і тому подібне.
Для більше точного визначення предмета математичної логіки варто було б уточнити, що мається на увазі під терміном логічно правильного висновку та як ставляться умови.. Щоб сформулювати хоча б одне тимчасове визначення, розглянемо приклад висновку. (Відповідно до традиційної форми записування, передумови відділяються від остаточного висновку горизонтальною рисою):
1.(Передумови) Якщо буде роздача премії, то ми виконали план.
Буде роздача премії.
(Остаточний висновок) Ми виконали план.
Якщо прийняти правильність передумов, то варто прийняти й правильність остаточного висновку. Інший, аналогічний приклад :
Якщо мені випаде туз, то я йду ва-банк.
Мені випав туз.
Я йду ва-банк.
Звичайно замість пропозицій (мені випав туз) і (я йду ва-банк) можуть бути записані будь-які такі дійсні пропозиції, значення яких може бути правильно або хибно; варто залишити незмінними тільки розташування слів «якщо» і «то» і розташування припущень, тобто структуру висновку. Нехай А і В позначає будь-які пропозиції, що заміняють. Структуру висновку можна виразити наступною схемою;
Якщо А, то В
А
В
Під визначенням, що дана схема являє собою (логічно правильну) схему висновків, мається на увазі наступне. Якщо замість А і В підставити такі пропозиції, що передумови, отримані в результаті заміни, будуть правильними, то й остаточний висновок буде правильним. Будь-яка людина, що розуміє значення союзів «якщо . . . то», зрозуміє, що це правильна схема висновку. У схемі висновку фігурують кілька слів з постійним значенням, далі кілька символів (букв) з мінливим значенням. Символи з мінливим значенням можуть бути змінними різних типів. Відповідно до їх типу замість символів можуть бути підставлені різні граматичні формації (наприклад: дійсні пропозиції, слова, що виражають властивості, назви предметів і т.д.). У попередньому прикладі змінні А і В заміняються тільки дійсними пропозиціями. На основі «регулярної» заміни змінних якоїсь (правильної) схеми висновку повинен виникати правильний висновок.
Але визначення «регулярної заміни» означає не тільки дотримання граматичних правил. У попередній схемі А і В можуть означати тільки такі дійсні пропозиції, правильність або хибність яких може бути вирішена однозначно. Такі дійсні пропозиції будемо називати висловленнями.
На основі будь-якої схеми висновку може бути отриманий правильний висновок тільки при дотриманні умов подібного характеру. Шляхом зміни умов можуть бути побудовані різні теорії логіки.
Найважливішими главами математичної логіки є калькуляція висловлень і калькуляція предикатів. У рамках даних глав може бути досліджена схема висновку в самому загальному випадку при найменшому числі умов.
В інших главах логіки розглядаються спеціальні схеми висновку, що є менш загальними.