
- •Томск-201
- •Введение
- •2. Оценка основных геометрических характеристик активной зоны.
- •3. Определение общего расхода теплоносителя через реактор и распределения расходов через отдельные твс.
- •4. Предварительный теплогидравлический расчет
- •5.Вариантные расчеты параметров размножающей среды для «холодного» реактора на начало кампании.
- •6. Расчёт изотопного состава в зависимости от времени работы реактора.
- •7. Оценка эффектов реактивности.
- •8.Обоснование выбора варианта, удовлетворяющего требованиям теплогидравлики и нейтронной физики.
- •9. Оценка эффективности системы регулирования
- •10.Расчет распределения основных теплотехнических параметров теплоносителя и материалов твэла по высоте а.З., оценка запасов до критических значений определяющих параметров.
- •11. Определение потерь давления при движении теплоносителя в пределах зоны
- •Список литературы
5.Вариантные расчеты параметров размножающей среды для «холодного» реактора на начало кампании.
5.1. Под обогащением С5 топлива в какой-либо зоне реактора будем подразумевать отношение:
 , (5.1
)
, (5.1
)
где N(5), N(8) -ядерные плотности соответственно 235U и 238U.
Обогащение С5 в первом приближении принимаем равным: в активной зоне С5=21% ; в торцевом и боковом экранах С5=0.72%.
После определения обогащения топлива в каждой зоне, находим ядерные плотности U238,U235, теплоносителя, кислорода, осколков деления, конструкционных материалов.
При среднеизотопном составе топлива ядерная плотность осколков деления может быть найдена по формуле[8]:
 ,
(5.2 )
,
(5.2 )
где
Р0
– допустимая норма накопления осколков
деления, Nт
– ядерная концентрация топлива, связанная
с массовой плотностью т
и мольной массой топлива Мт
соотношением:
т
и мольной массой топлива Мт
соотношением:
 см-3
- ядерная концентрация топлива в
активной зоне к началу компании.
см-3
- ядерная концентрация топлива в
активной зоне к началу компании.
 ,
см-3
;
,
см-3
;
 ,
см-3.
,
см-3.
kz – аксиальный коэффициент неравномерности тепловыделения:
 .
.
= 0.1·7.124·1021 ·270/ 2 ·1.245·239 = 2,636·1020 см-3.
При найденных значениях С5 и N(оск) ядерная плотность 238U и 235U определяются по формулам:
 ,
см-3
;
,
см-3
;
 ,
см-3,
,
см-3,
где Nт' - ядерная концентрация топлива в активной зоне к концу компании, для оксидного топлива равная:
 =
7.124·1021
( 1 – (0.1/2·1.245) = 6,838·1021
, см –3
.
=
7.124·1021
( 1 – (0.1/2·1.245) = 6,838·1021
, см –3
.
Концентрация кислорода N(о) определяется как:
N(о)=2Nт = 2·7.124·1021 = 1,425 ·1022, см-3 .
Для ядерных плотностей элементов, не входящих в состав топливного блока (теплоносителя - N(тепл), конструкционных материалов - N(км)), имеем:
 =
(0.804·6.02·1023/23)·0.33
= 6.9·1021
,см-3,
=
(0.804·6.02·1023/23)·0.33
= 6.9·1021
,см-3,
 =
(8.26·6.02·1023/140)·0.281
= 9,9·1021
, см-3.
=
(8.26·6.02·1023/140)·0.281
= 9,9·1021
, см-3.
По формулам, рассмотренным выше, определяем ядерные плотности всех составляющих бокового и торцевого экрана. Полученные значения заносим в таблицу.
Таблицу.5.1 Таблица «ядерные плотности всех составляющих различных зон» .
|
|
|
|
|
|
N(о) |
|
|
Ак.З |
|
2,636· 1020 |
1,496* 1021 |
|
6,838·1021 |
1,425 ·1022 |
6.9·1021 |
9,9·1021 |
ТЭ |
1.867*1022 |
6.139* 10^20 |
1.254* 10^20 |
1.779*10^22 |
1.792*1022 |
- |
6.941*10^21 |
9.964* 10^21 |
БЭ |
2,96*1022 |
9,74* 1020 |
1,989* 1020 |
2,8* 1022 |
2,8*1022 |
- |
3,64·1021 |
7,4·1021 |
5.2.
Расчёт многогрупповых спектров нейтронов
начинается с определения макроскопических
сечений. По известным ядерным плотностям
Nј
элементов и восьмигрупповым микросечениям
рассчитываем в каждой зоне реактора
для k–ой
группы нейтронов макроскопические
сечения захвата ,
деления
,
деления
 ,
полного увода
,
полного увода
 из k-ой
группы и перевода нейтронов
из k-ой
группы и перевода нейтронов
 из k-ой
группы в l-ю
группу, транспортное сечение
из k-ой
группы в l-ю
группу, транспортное сечение
 и произведение числа вторичных нейтронов
на сечение деления
и произведение числа вторичных нейтронов
на сечение деления
 [6]:
[6]:
 ,
,
 ,
,
где
суммирование проводится по всем j-м
элементам в зоне, а индекс р
характеризует тип процесса взаимодействия
-с,
-f,
-d,
-tr,
-a, -ad.
Затем определяем коэффициент диффузии
D(k),
а также сечение поглощения
 ,
полного увода нейтронов
из k-ой
группы в нижележащие, полного увода и
поглощения
,
полного увода нейтронов
из k-ой
группы в нижележащие, полного увода и
поглощения
 :
:
 ;
;
 ;
;
 ;
;
 ,
,
где n- число энергетических групп.
По
выше указанным формулам определяем
суммарные макросечения для всех зон
(активная зона, боковые экраны и торцевая
зона). Полученные значения заносятся в
таблицы . Необходимые микросечения
берутся из
 по
восьми группам. Необходимые ядерные
плотности – из таблицы (5.1).
по
восьми группам. Необходимые ядерные
плотности – из таблицы (5.1).
Таблица 5.2 «Макросечения элементов активной зоны»
|
кtr, см-1 |
ck, см-1 |
fk, см-1 |
fkfk·, см-1· |
dk, см-1 |
ak, см-1 |
ad, см-1
|
D(k) |
1 |
0.058 |
4.446* 10^-4 |
5.077* 10^-3 |
0.015 |
0.022 |
5.522* 10^-3 |
0.027 |
5.703 |
2 |
0.09 |
6.352* 10^-4 |
3.145* 10^-3 |
8.136* 10^-3 |
0.023 |
3.781* 10^-3 |
0.026 |
3.693 |
3 |
0.123 |
9.036* 10^-4 |
2.017* 10^-3 |
5.002* 10^-3 |
0.016 |
2.921* 10^-3 |
0.019 |
2.702 |
4 |
0.144 |
1.379* 10^-3 |
2.393* 10^-3 |
5.839* 10^-3 |
0.011 |
3.772* 10^-3 |
0.014 |
2.311 |
5 |
0.163 |
2.346* 10^-3 |
2.974* 10^-3 |
7.228* 10^-3 |
0.559 |
5.321* 10^-3 |
0.565 |
2.049 |
6 |
0.171 |
3.939* 10^-3 |
3.692* 10^-3 |
8.936* 10^-3 |
8.007* 10^-3 |
7.631* 10^-3 |
0.016 |
1.945 |
7 |
0.204 |
7.446* 10^-3 |
7.453* 10^-3 |
0.018 |
1.211* 10^-3 |
0.015 |
0.016 |
1.632 |
8 |
0.194 |
0.012 |
0.026 |
0.062 |
- |
0.038 |
0.038 |
1.72 |
Таблица 5.3 «Макросечения элементов торцевой зоны»
|
кtr, см-1 |
ck, см-1 |
fk, см-1 |
fkfk·, см-1· |
dk, см-1 |
ak, см-1 |
ad, см-1
|
D(k) |
1 |
0.091 |
2.299* 10^-4 |
0.01 |
0.03 |
0.047 |
0.011 |
0.058 |
3.646 |
2 |
0.107 |
1.657* 10^-3 |
3.714* 10^-3 |
9.584* 10^-3 |
0.033 |
5.371* 10^-3 |
0.038 |
3.128 |
3 |
0.144 |
2.05* 10^-3 |
1.48* 10^-4 |
3.67* 10^-4 |
0.01 |
2.198* 10^-3 |
0.012 |
2.311 |
4 |
0.198 |
2.845* 10^-3 |
1.756* 10^-4 |
4.284* 10^-4 |
7.485* 10^-3 |
3.02* 10^-3 |
0.011 |
1.68 |
5 |
0.246 |
4.933* 10^-3 |
2.182* 10^-4 |
5.303* 10^-4 |
6.129* 10^-3 |
5.151* 10^-3 |
0.011 |
1.355 |
6 |
0.264 |
8.867* 10^-3 |
2.709* 10^-4 |
6.556* 10^-4 |
3.822* 10^-3 |
9.138* 10^-3 |
0.013 |
1.26 |
7 |
0.297 |
0.016 |
5.468* 10^-4 |
1.323* 10^-3 |
4.814* 10^-4 |
0.016 |
0.017 |
1.121 |
8 |
0.239 |
9.441* 10^-3 |
1.889* 10^-3 |
4.571* 10^-3 |
- |
0.011 |
0.011 |
1.392 |
Таблица5.4 «Макросечения элементов боковой зоны»
|
кtr, см-1 |
ck, см-1 |
fk, см-1 |
fkfk·, см-1· |
dk, см-1 |
ak, см-1 |
ad, см-1
|
D(k) |
1 |
0.134 |
3.278* 10^-4 |
0.017 |
0.048 |
0.071 |
0.017 |
0.088 |
2.488 |
2 |
0.153 |
2.627* 10^-3 |
5.891* 10^-3 |
0.015 |
0.047 |
8.518* 10^-3 |
0.055 |
2.181 |
3 |
0.202 |
3.249* 10^-3 |
2.348* 10^-4 |
5.822* 10^-4
|
0.013 |
3.484* 10^-3 |
0.016 |
1.648 |
4 |
0.289 |
4.505* 10^-3 |
2.785* 10^-4 |
6.796* 10^-4 |
9.735* 10^-3 |
4.784* 10^-3 |
0.015 |
1.154 |
5 |
0.361 |
7.817* 10^-3 |
3.462* 10^-4 |
8.412* 10^-4 |
7.143* 10^-3 |
8.163* 10^-3
|
0.015 |
0.924 |
6 |
0.391 |
0.014 |
4.297* 10^-4 |
1.04* 10^-3 |
3.852* 10^-3 |
0.014 |
0.018 |
0.853 |
7 |
0.418 |
0.025 |
8.674* 10^-4 |
2.099* 10^-3 |
4.687* 10^-4 |
0.026 |
0.026 |
0.798 |
8 |
0.356 |
0.015 |
2.996* 10^-3 |
7.251* 10^-3 |
- |
0.018 |
0.018 |
0.936 |
Уравнения для групповых интегральных потоков в активной зоне имеют вид[6]:

 ,
,
где
 - геометрический параметр; j
– номер ядра делящегося нуклида; k
– номер энергетической группы; χ(k)
– доля нейтронов в спектре деления,
попадающая в k-ю
группу.
- геометрический параметр; j
– номер ядра делящегося нуклида; k
– номер энергетической группы; χ(k)
– доля нейтронов в спектре деления,
попадающая в k-ю
группу.
Если теперь рассмотреть реактор с торцовым отражателем и учесть в них равенство потоков, то уравнение для токов нейтронов в этом случае можно представить:
 .
.
Толщина торцового экрана считается достаточно большой, чтобы не учитывать утечку нейтронов из него в направлении оси z. Аналогичным образом записывается уравнение для интегральных потоков в боковом экране:
 .
.
Уравнение должно решаться на макроконстантах бокового экрана при найденной утечке нейтронов из активной зоны и торцового экрана в боковой экран. Утечка нейтронов из бокового экрана в радиальном и аксиальном направлениях считается пренебрежимо малой.
Уравнение для радиального и аксиального геометрических параметров:

 ,
,
где – материальный параметр активной зоны.
В процессе нейтронно-физического расчёта уравнения решаются совместно при условии критичности
 .
.
Ниже
приводится одна из возможных схем
решения этих уравнений. Для предварительно
заданных
 и
и
 равными по 20 см и концентрации делящегося
элемента в активной зоне находятся
равными по 20 см и концентрации делящегося
элемента в активной зоне находятся
 и
и
 .
Затем решается уравнение для интегральных
потоков. При этом в активной зоне
интегральные потоки нормируются в
соответствии с равенством:
.
Затем решается уравнение для интегральных
потоков. При этом в активной зоне
интегральные потоки нормируются в
соответствии с равенством:
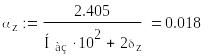 ,см-1.
,см-1.
![]() ,см-1.
,см-1.
 ,
,
что подразумевает также нормировку скорости генерации нейтронов на единицу. Уравнение можно представить в виде:

При этом для первой группы следует, что J(0)=0, [J(k)]=см.
На данном этапе считая, что спектры нейтронов в активных зонах совпадают и слабо зависят от эффективных добавок экранов рассчитывают спектр нейтронов в активной зоне, начиная с первой группы.
 =
11.9,
см;
=
11.9,
см;
 =20.5,
см;
=20.5,
см;
 =38,
см;
=38,
см;
 =64,
см ;
=64,
см ;
 =1,5,
см;
=1,5,
см;
 =1,7,
см;
=1,7,
см;
 =2,
см;
=2,
см; =0,24,
см,
=0,24,
см,
где χ(k) – доля нейтронов в спектре деления, попадающая в k-ю группу.
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
, D(k) берутся из таблицы .
Эффективный коэффициент размножения нейтронов:
 =
0,998.
=
0,998.
Т.к. [1-kэфф]<0.01, то можем считать , что обогащение принято верно.
Далее
оцениваем спектры в
торцовом
 и боковом
и боковом
 экранах .
экранах .
Для торцового экрана:

Для бокового экрана:
 ,
,
где ;
для k
= 3 , 4и т.д.
;
для k
= 3 , 4и т.д.
 .
.
В соотношениях учитывается, что в экранах лишь нейтроны первой и второй групп могут вызвать деление U8.
Групповые спектры деления Ji(к) :
Таблица 5.6.
-
Зона(i)
1
2
3
4
5
6
7
8
Ак.З
11,9
20,5
38
64
1,5
1,7
2
0,24
Т.Э
0.595
2,28
4,22
23
1,775
1,9
1,823
0,55
Б.Э
0.238
1,37
2,13
10,7
0,75
0,89
0,612
0,267
По найденным спектрам нейтронов J(k) определяется для каждой зоны (активная зона, боковой и торцовой экраны) одногрупповые микросечения элементов:
 ;
; 
где р – означает тип взаимодействия (c, f, d, tr), j – химический элемент активной зоны. Среднее значение коэффициента диффузии для i-х зон реактора определяют из формулы :
 .
.
Определение микроскопических сечений и коэффициента диффузии в активной зоне:
Микросечения захвата.






Транспортные микросечения элементов активной зоны.






Микросечения деления.


Произведение числа вторичных нейтронов на сечение деления .

 5)
Коэффициент
диффузии в активной зоне, см.
5)
Коэффициент
диффузии в активной зоне, см.
 .
.
Аналогичным образом определяем усредненные микросечения элементов торцевых и бокового экранов. Полученные значения заносим в таблицу.
Таблица5.7. «Одногрупповые микросечения элементов р,j, 10-24 см-2и усреднённые коэффициенты диффузии».
Зона |
р |
U8 |
U5 |
осколки |
О16 |
Na23 |
КМ |
|
|
|
|
|
|||||
|
tr |
7.524 |
7.332 |
10.924 |
3.397 |
3.23 |
2.805 |
|
|
|
|
|
|||||
|
c |
0.134 |
0.262 |
0.159 |
1.702* 10^-3 |
1.186* 10^-3 |
6.97* 10^-3
|
|
|
|
|
|
|||||
аз. |
f |
0.079 |
1.381 |
- |
- |
- |
- |
|
|
|
|
|
|||||
|
if |
0.219 |
3.455 |
- |
- |
- |
- |
|
|
|
|
|
|||||
|
D.ср |
2,891 |
|
|
|
|
|
||||||||||
|
tr |
9.095 |
9.327 |
12.564 |
3.649 |
3.627 |
3.467 |
|
|
|
|
|
|||||
|
c |
0.201 |
0.472 |
0.241 |
3.295* 10^-4 |
1.451* 10^-3 |
7.847* 10^-3 |
|
|
|
|
|
|||||
Т.Э. |
f |
0.022 |
1.774 |
- |
- |
- |
- |
|
|
|
|
|
|||||
|
if |
0.06 |
4.342 |
- |
- |
- |
- |
|
|
|
|
|
|||||
D.ср |
1.807 |
|
|
|
|
|
|||||||||||
Б.Э. |
tr |
8.938 |
9.121 |
12.411 |
3.64 |
3.555 |
3.39 |
|
|
|
|
|
|||||
c |
0.19 |
0.45 |
0.232 |
2.807* 10^-4 |
1.315* 10^-3 |
7.391* 10^-3 |
|
|
|
|
|
||||||
f |
0.024 |
1.734 |
- |
- |
- |
- |
|
|
|
|
|
||||||
if |
0.065 |
4.249 |
- |
- |
- |
- |
|
|
|
|
|
||||||
D.ср |
1.275 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||
В дальнейшем расчёте будут использоваться усреднённые значения.
5.3. Расчёт коэффициента размножения бесконечной среды.
Физический коэффициент размножения характеризует отношение числа нейтронов в данном поколении к числу нейтронов в предыдущем. Коэффициент размножения бесконечной среды К∞ является очень важным параметром активной зоны реактора и даёт вероятностное описание ценной реакции без учёта утечек нейтронов. Расчет производится по формуле четырёх сомножителей [4].
 ,
,
где νa – среднее число вторичных быстрых нейтронов, рождающихся в результате захвата быстрого нейтрона в U235 или Pu239 ;
μ – коэффициент, учитывающий увеличение числа замедлившихся нейтронов за счёт размножения на быстрых в результате деления ядер U238 или Th232 ;
φ – вероятность избежать резонансного захвата при замедлении в тепловую группу. Данный коэффициент в этой работе не учитывается, т.к число ннейтронов замедлившихся до тепловых энергий будет пренебрежимо мало.
Θ – коэффициент использования быстрых нейтронов.
В начале работы свежего реактора, когда в активной зоне присутствуют только один делящийся изотоп U235 и один тип тепловыделяющего элемента, среднее число вторичных нейтронов определяется выражением: [1]
 ,
,
которое учитывает непроизводительный радиационный захват быстрого нейтрона ядрами U235 и U238.
Для
активной зоны:
Для
торцевого экрана:
 ,
,
Для
зоны воспроизводства:
 .
.
Вычисление коэффициента размножения на быстрых нейтронах.
Результаты расчётов описываются формулой [1]:
 ,
где
,
где
 усреднённые
по ячейке макросечения увода и деления.
усреднённые
по ячейке макросечения увода и деления.
 ,см-1
.
,см-1
.
Для активной зоны:
![]()
 .
. .
.
. .
Следовательно
 .
.
Для торцевого экрана:

Следовательно
 .
.
Для бокового экрана:

Следовательно
 .
.
Коэффициент использования быстрых нейтронов [4]:
 ;
;
Для
активной зоны:
 Для
торцевого экрана:
Для
торцевого экрана:

Для бокового экрана:

Возраст нейтронов [4]:
 ,
,
где
n-
число групп, D-
коэффициент диффузии,
 -
объёмные доли компонентов,
-
объёмные доли компонентов,
 -
макросечения поглощения и полного
увода.
-
макросечения поглощения и полного
увода.
В данной работе воспользуемся ранее усреднёнными величинами.
Для
активной зоны:

Для торцевых экранов:

Для зоны воспроизводства:

Эффективный коэффициент размножения и реактивность.
По определению эффективный коэффициент размножения учитывает процессы размножения и поглощения, а также утечки быстрых нейтронов в среде конечных размеров:
 ,
,
где
 ,
,
 –
вероятности того, что нейтрон избежит
утечки из реактора в процессе замедления
и диффузии. Процессом диффузии
пренембрегаем.
–
вероятности того, что нейтрон избежит
утечки из реактора в процессе замедления
и диффузии. Процессом диффузии
пренембрегаем.
 ,
,
и тогда Кэф определяется формулой [4]:
 .
.
 ,
,
 – радиальный и высотный геометрические
параметры. Эффективные добавки бокового
– радиальный и высотный геометрические
параметры. Эффективные добавки бокового
 и торцового
и торцового
 экранов могут быть определены из условий
сшивки токов и потоков нейтронов на
соответствующих границах с активной
зоной [3]
экранов могут быть определены из условий
сшивки токов и потоков нейтронов на
соответствующих границах с активной
зоной [3]

 ,
,
где
 ;
;
 ;
;
 ;
;

 ;
;

 =40,см
и
=40,см
и
![]() =50,см – толщины торцового и бокового
экранов ( в см);
=50,см – толщины торцового и бокового
экранов ( в см);
J0 и J1 – функции Бесселя первого рода для действительного аргумента нулевого и первого порядка [3];
K0 и K1 – функции Бесселя второго рода для мнимого аргумента нулевого и первого порядка [3];
Материальных
параметров бокового ( )
и торцевого (
)
и торцевого ( )
экранов:
)
экранов:
= ,см-2
,
,см-2
,
= ,
см-2
,
см-2
![]()
![]()
![]()
![]()
 ,
,
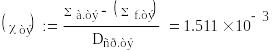 .
.
Система решений решается графически. Решения уравнений будут определять геометрический параметр.
Первое уравнение имеет решение в точки (0,5;1.2). Т.е Z=1,2. Тогда

Второе
уравнение: (1,5;1,25). У=1.25. Тогда

Тогда
геометрический параметр
 определяем как [3]:
определяем как [3]:

 ;
;
Для
активной зоны:


Для
торцевого экрана:


Для
бокового экрана:











