Задания для самостоятельной работы

Составить программы для решения следующих задач:

Варианты заданий:

Вариант 1.

1. Определить количество цифр в представлении натурального числа N в семеричной системе.

2. Вычислить сумму ряда с погрешностью в окрестности точки ноль, т.е. при :

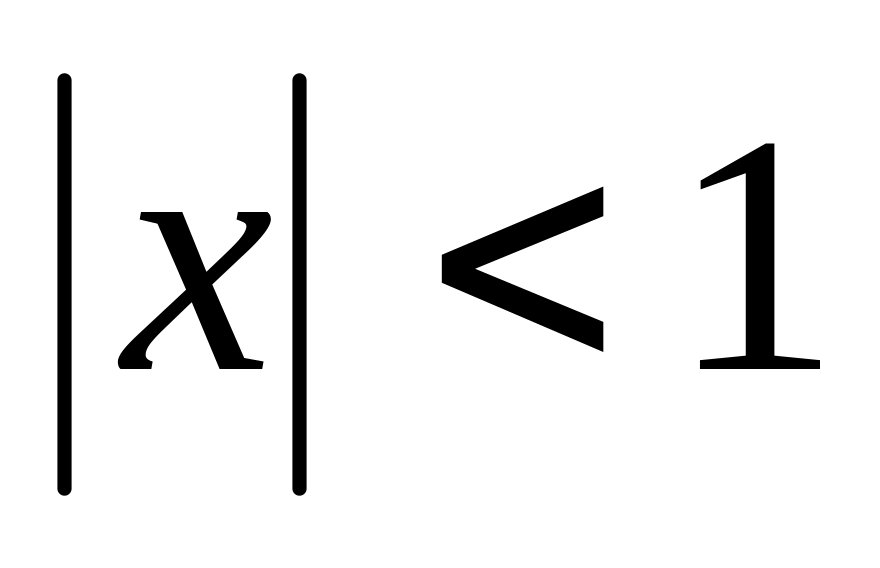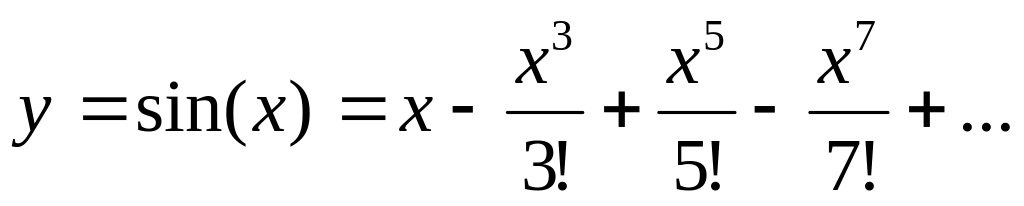
3. Вычислить значение выражения:

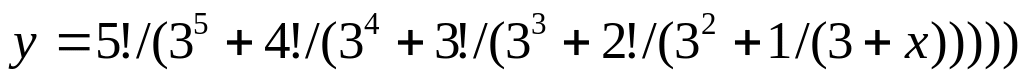
4. Дано целое 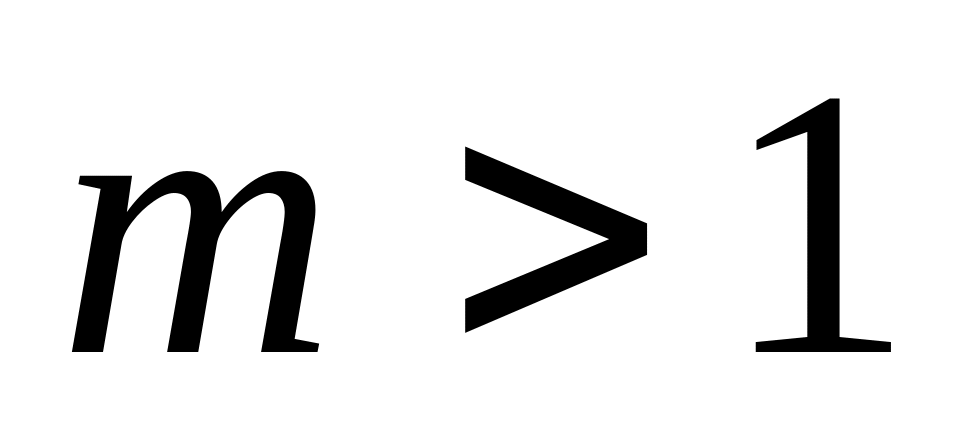. Получить наибольшее целое k, при котором .

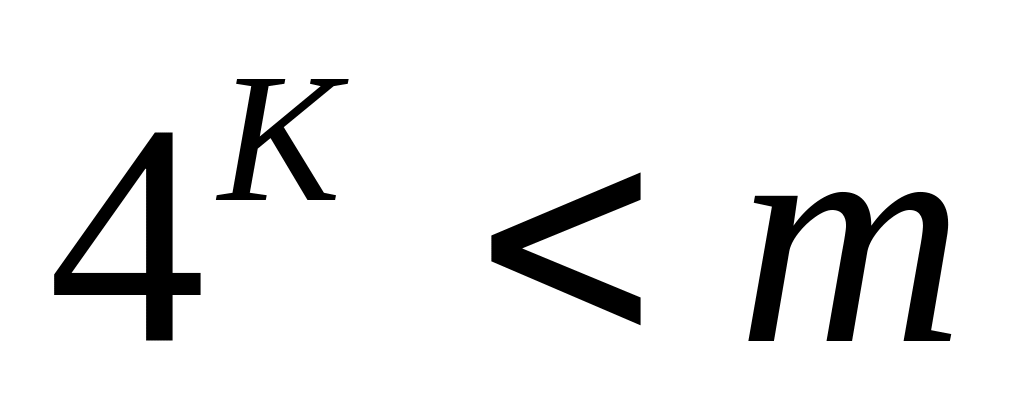Вариант 2.

1. Определить, каких цифр больше в двоичном представлении натурального числа N – нулей или единиц.

2. Вычислить сумму ряда с погрешностью в окрестности точки ноль, т.е. при :

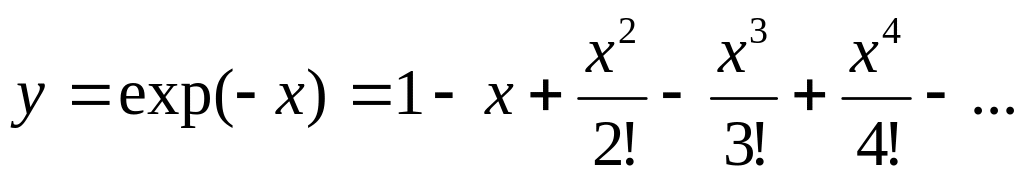
3. Вычислить значение выражения:

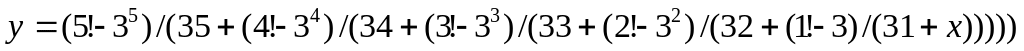
4. Определить, является ли заданное натуральное число простым.

Вариант 3.

1. Определить наибольшую цифру среди цифр натурального числа N.

2. Вычислить сумму ряда с погрешностью в окрестности точки ноль, т.е. при :

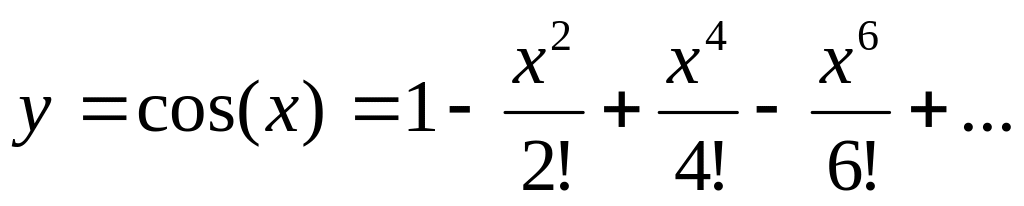
3. Вычислить значение выражения:

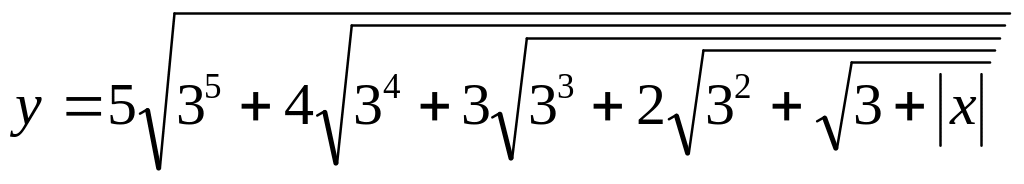
4. Числа Фибоначч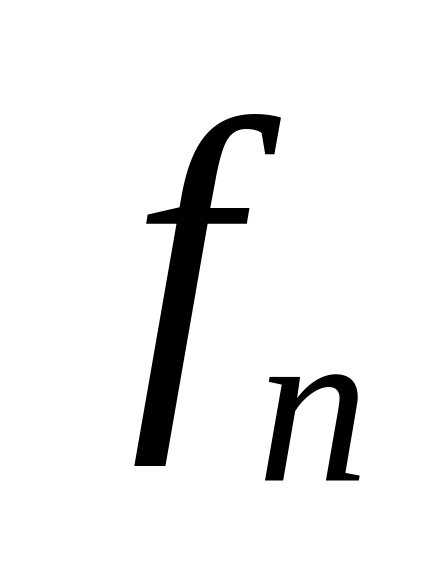и определяются формулами:

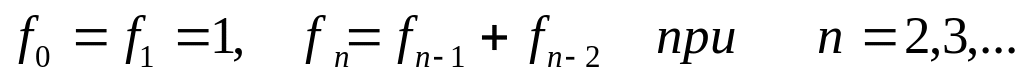
Определить - k число Фибоначчи (k>1).

Вариант 4.

1. Поменять местами первую и последнюю цифры в натуральном числе N.

2. Вычислить сумму ряда с погрешностью в окрестности точки ноль, т.е. при :

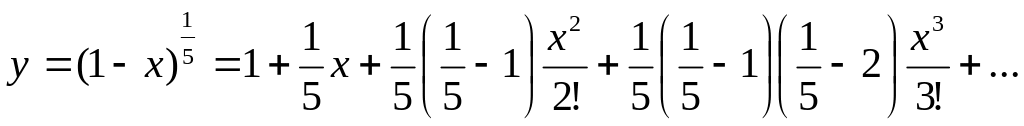
3. Вычислить значение выражения:

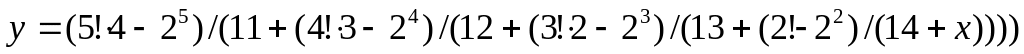
4. Дано натуральное число N. Получить наименьшее целое число вида 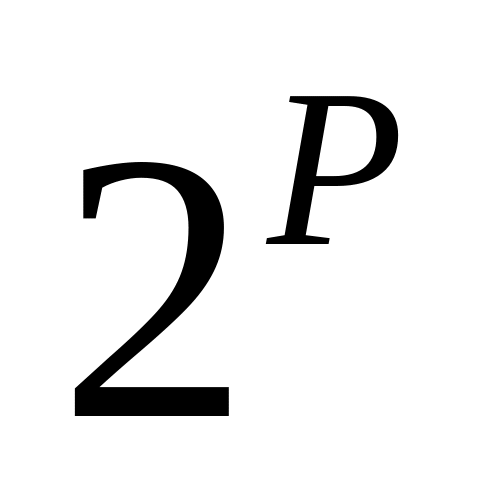, превосходящее N.

Вариант 5.

1. Получить сумму первой и последней цифры натурального числа N.

2. Вычислить сумму ряда с погрешностью в окрестности точки ноль, т.е. при :

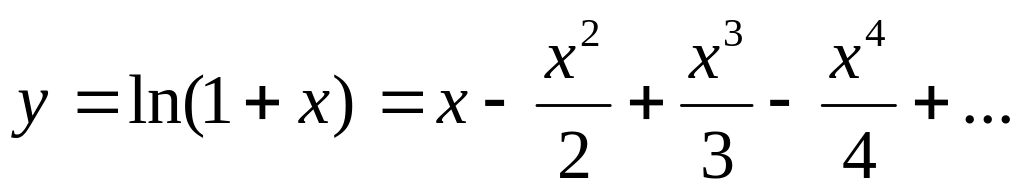
3. Вычислить значение выражения:

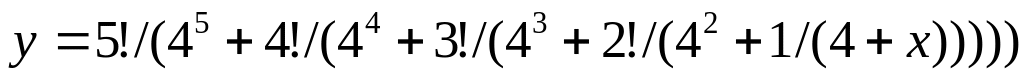
4. Определить, является ли заданное натуральное число N совершенным, т.е. равным сумме всех своих (положительных) делителей, кроме самого себя.

Вариант 6.

1. Определить, имеется ли среди цифр натурального числа N, представленного в восьмеричной системе, хотя бы одна единица.

2. Вычислить сумму ряда с погрешностью в окрестности точки ноль, т.е. при :

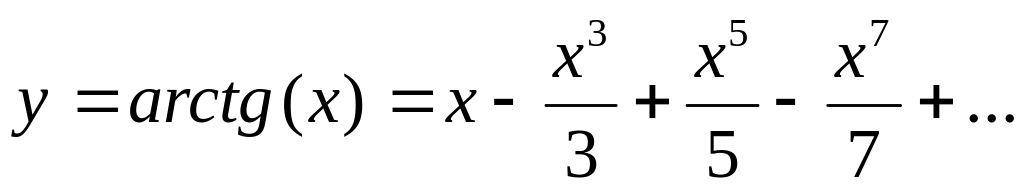
3. Вычислить значение выражения:

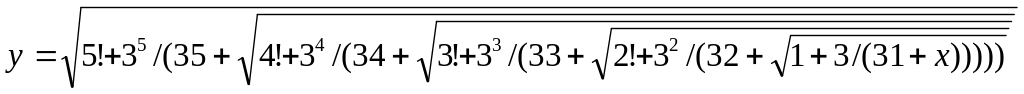
4. Числа Фибоначчи определяются формулами:

Вычислить сумму всех чисел Фибоначчи, которые не превосходят заданного целого числа m.

Вариант 7.

1. Определить, все ли цифры натурального числа N являются одинаковыми.

2. Вычислить сумму ряда с погрешностью в окрестности точки ноль, т.е. при :

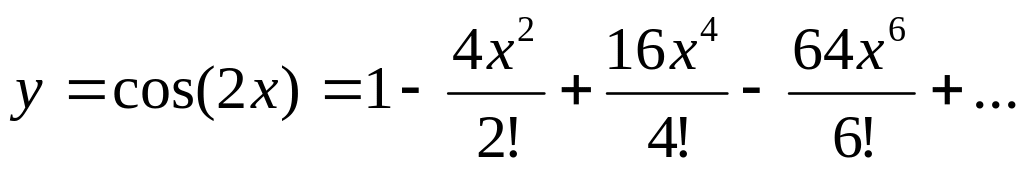
3. Вычислить значение выражения:

4. Спортсмен в первый день пробежал 10 км. Каждый следующий день он увеличивал дневную норму на 10 % от нормы предыдущего дня. Какой путь пробежит спортсмен в седьмой день?

Вариант 8.

1. Определить разность между наибольшей и наименьшей цифрами натурального числа N.

2. Вычислить сумму ряда с погрешностью в окрестности точки ноль, т.е. при :

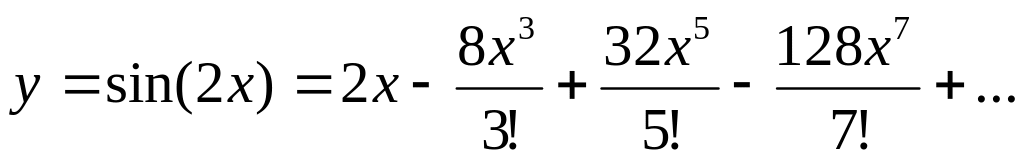
3. Вычислить значение выражения:

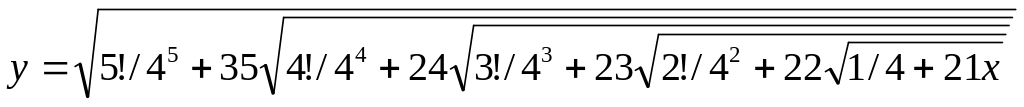
4. Пусть N – натуральное число. Вычислить:

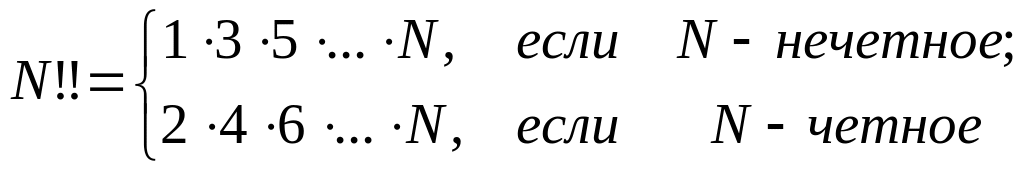
Вариант 9.

1. Определить все цифры натурального числа N в шестнадцатиричной системе счисления.

2. Вычислить сумму ряда с погрешностью в окрестности точки ноль, т.е. при :

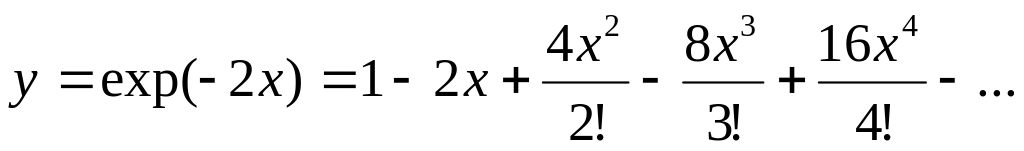
3. Вычислить значение выражения:

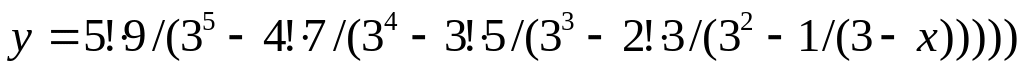
4. Дано целое m>1. Получить наибольшее число 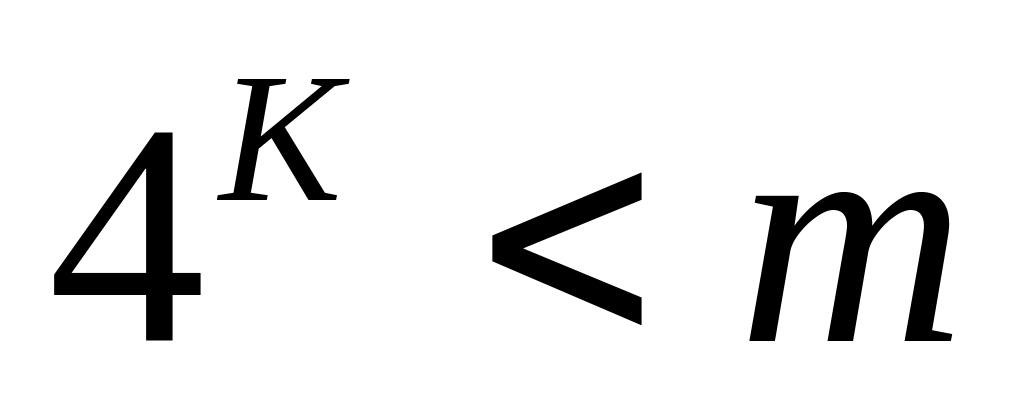, где k – целое число.

Вариант 10.

1. Поменять порядок цифр натурального числа N на обратный порядок.

2. Вычислить сумму ряда с погрешностью :

3. Вычислить значение выражения:

4. Пусть N – натуральное число. Вычислить:

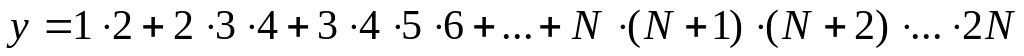
Вариант 11.

1. Определить, расположены ли цифры натурального числа N в порядке возрастания.

2. Вычислить сумму ряда с погрешностью в окрестности точки ноль, т.е. при :

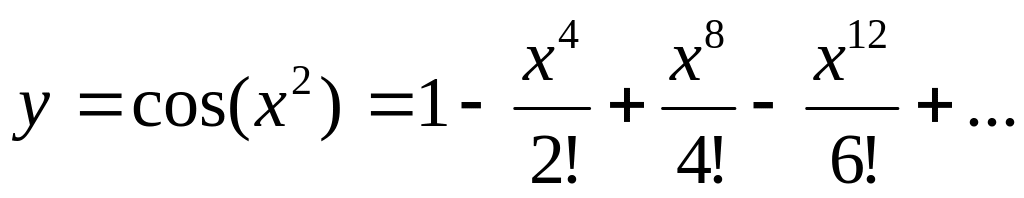
3. Вычислить значение выражения:

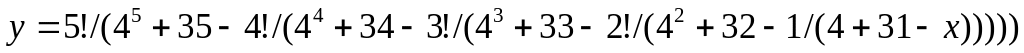
4. Числа Фибоначчи определяются формулами:

Найти первое по порядку число Фибоначчи, большее заданного m (m>1).

Вариант 12.

1. Определить номер первой по порядку цифры натурального числа N, имеющей наименьшее значение.

2. Вычислить сумму ряда с погрешностью в окрестности точки ноль, т.е. при :

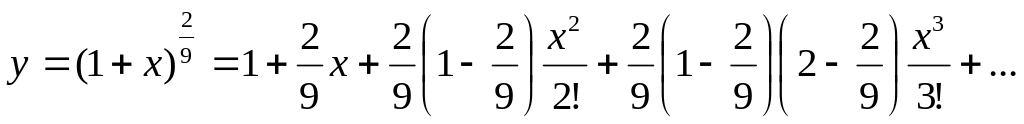
3. Вычислить значение выражения:

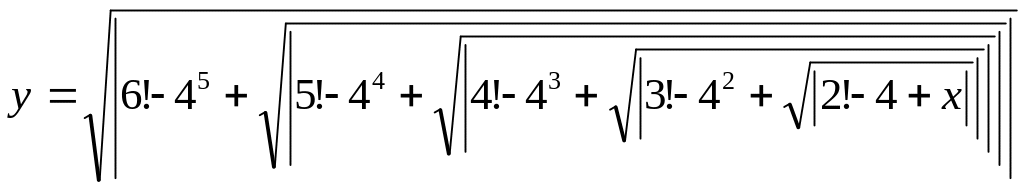
4. Дано натуральное число N. Получить наименьшее целое число k, при котором .

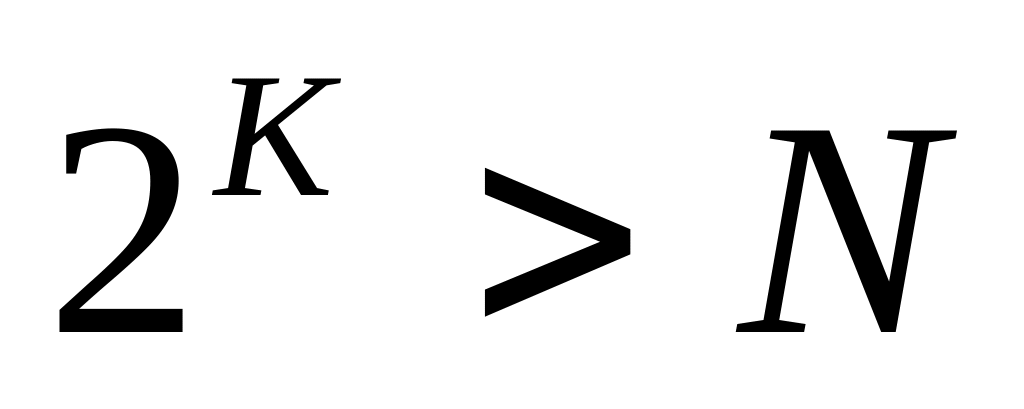Вариант 13.

1. Подсчитать количество цифр, больших 9, у натурального числа N в шестнадцатеричной системе счисления.

2. Вычислить сумму ряда с погрешностью в окрестности точки ноль, т.е. при :

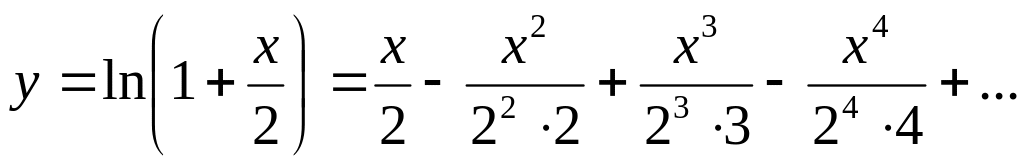
3. Вычислить значение выражения:

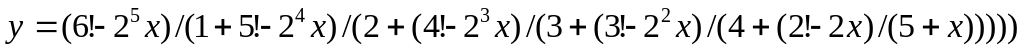
4. Дано натуральное число N. Вычислить:

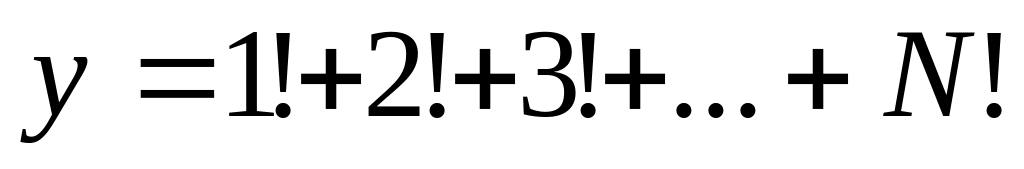
Вариант 14.

1. Получить среднее арифметическое всех цифр натурального числа N .

2. Вычислить сумму ряда с погрешностью в окрестности точки ноль, т.е. при :

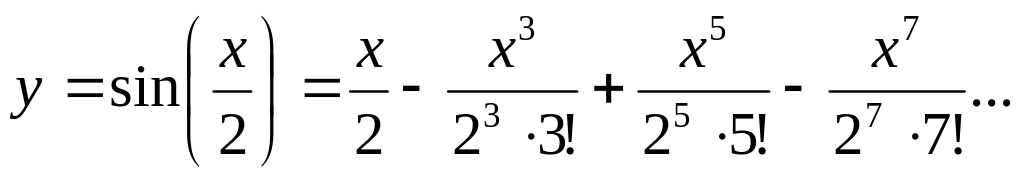
3. Вычислить значение выражения:

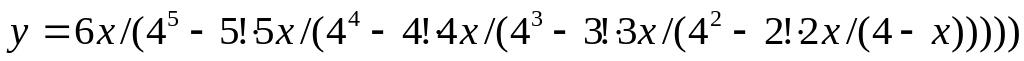
4. Некая сумма денег S помещена в сберкассу под процент T. Через сколько лет она удвоится?

Вариант 15.

1. Определить, в какой из систем счисления сумма всех цифр натурального числа N имеет наибольшее значение. Основания систем счисления: 2, 3, …, 9.

2. Вычислить сумму ряда с погрешностью в окрестности точки ноль, т.е. при :

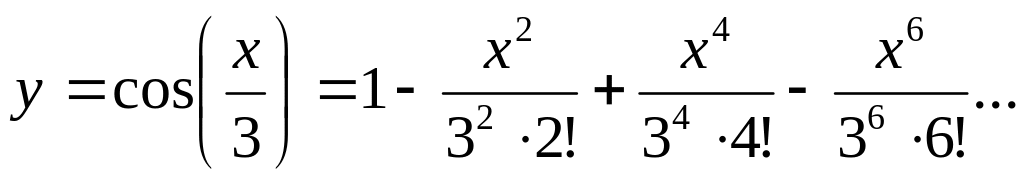
3. Вычислить значение выражения:

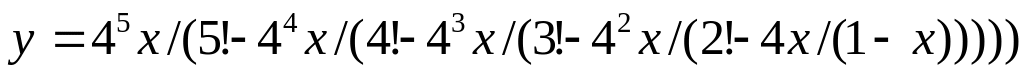
4. Дано натуральное число N. Найти все его простые положительные делители.