
6. Одноканальная смо с ожиданием
На вход заявки поступают с интенсивностью . Канал может обслуживать заявки с интенсивностью . Если канал занят, то вновь поступающая заявка становится в очередь. Имеем состояния:
s0 – канал свободен, вероятность состояния р0,
s1 – канал занят, очереди нет, вероятность состояния р1,
s2 – канал занят, в очереди 1 заявка, вероятность состояния р2,
s3 – канал занят, в очереди 2 заявки, вероятность состояния р3, …
sk – канал занят, в очереди (k – 1) заявка, вероятность состояния рk, …
где р0 + р1 + р2 + р3 + … = 1.
Строим диаграмму смены состояний системы:

Составляем балансные уравнения:
s0: р0 = mр1, т.е. р1 = = qр0;
s1:
р0
+ mр2
=mр1
+ р1
р2
=
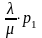 = qр1
= q
2р0;
= qр1
= q
2р0;
s2:
р1
+ mр3
=mр2
+ р2
р3
=
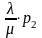 = qр2
= q
3р0;
= qр2
= q
3р0;
… рk = q kр0; …
Подставляем полученные значения вероятностей в условие р0 + р1 + р2 + р3 + … = 1:
р0 + qр0 + q 2р0 + q 3р0 + … = 1 р0(1 + q + q 2 + q 3 +…) = 1.
Поскольку степенной ряд сходится (т.е. сумма в скобках должна быть суммой членов бесконечно убывающей геометрической прогрессии), то получаем ограничение на q: = / < 1, т.е. для устойчивости работы СМО необходимо, чтобы выполнялось неравенство < , в противном случае нарушится условие: каждая заявка, поступившая на вход СМО с ожиданием, будет обслужена за конечное среднее время.
Поскольку сумма
членов бесконечно убывающей геометрической
прогрессии со знаменателем q
равна S
=
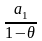 или р0(1
+
q
+
q
2 +
q
3 +…) = р0
= 1,
где а1
– 1-й член прогрессии, то р0
= 1 – q,
а рk
= q
k(1
– q).
или р0(1
+
q
+
q
2 +
q
3 +…) = р0
= 1,
где а1
– 1-й член прогрессии, то р0
= 1 – q,
а рk
= q
k(1
– q).
Средняя длина
очереди
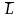 в одноканальной СМО с ожиданием, т.е.
математическое ожидание числа заявок
в очереди:
= 1р2
+ 2р3
+ 3р4
+… =
2/(1 – ).
в одноканальной СМО с ожиданием, т.е.
математическое ожидание числа заявок
в очереди:
= 1р2
+ 2р3
+ 3р4
+… =
2/(1 – ).
Среднее число
заявок (клиентов) в одноканальной СМО
с ожиданием
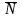 ,
которое включает среднее число заявок
в очереди
и среднее число заявок, находящихся на
обслуживании. Для второй средней имеем:
число заявок на обслуживании равно 0,
если канал свободен, т.е. с вероятностью
р0
= 1 – ,
и равно 1 во всех остальных состояниях,
т.е. с вероятностью 1 – р0
=
. Следовательно,
=
+
=
+
2/(1 – )
= /(1
– ).
,
которое включает среднее число заявок
в очереди
и среднее число заявок, находящихся на
обслуживании. Для второй средней имеем:
число заявок на обслуживании равно 0,
если канал свободен, т.е. с вероятностью
р0
= 1 – ,
и равно 1 во всех остальных состояниях,
т.е. с вероятностью 1 – р0
=
. Следовательно,
=
+
=
+
2/(1 – )
= /(1
– ).
7. Замкнутые смо
Частным случаем СМО с ожиданием являются замкнутые СМО, обслуживающие заявки ограниченного числа постоянных клиентов N0, поэтому интенсивность входящего на вход потока заявок будет уменьшаться с увеличением числа заявок, находящихся в СМО.
Рассмотрим замкнутую систему обслуживания, в которой возможными «клиентами» являются N0 единиц однотипного оборудования на конкретном предприятии. Пусть средняя частота отказа каждого образца оборудования в ед. времени равна λ, ремонт оборудования осуществляют п специалистов с одинаковой производительностью μ единиц оборудования в ед. времени.
Имеем п-канальную систему обслуживания, в которой каждое выходящее из строя оборудование подлежит ремонту. Каждый работающий образец оборудования определяет поток заявок (отказов в работе) с интенсивностью λ, среднее время ремонта оборудования 1/μ. Оборудование после устранения в нем неисправности снова инициирует поток заявок.
Имеем следующие состояния замкнутой СМО:
s0 – неисправного оборудования нет; вероятность р0;
s1 – неисправного оборудования 1 ед., очереди нет; вероятность р1;
s2 – неисправного оборудования 2 ед., очереди нет; вероятность р2;
…
sn – неисправного оборудования n ед., очереди нет; вероятность рn;
sn + 1 – неисправного оборудования n + 1 ед., в очереди 1 ед. оборудования; вероятность рn+1;
sn + 2 – неисправного оборудования n + 2 ед., в очереди 2 ед. оборудования; вероятность рn+2;
…
sN0 – неисправного оборудования N0 ед., в очереди N0 – n ед. оборудования; вероятность рN0.
Строим диаграмму смены состояний СМО:

Состояние
sk
определяется числом k
неработающих единиц оборудования,
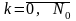 .
Интенсивность потоков с учетом того,
что если k
ед. оборудования
неисправно, то эксплуатируется N0
– k
ед. оборудования:
.
Интенсивность потоков с учетом того,
что если k
ед. оборудования
неисправно, то эксплуатируется N0
– k
ед. оборудования:
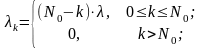
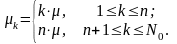
Балансные уравнения для соответствующих состояний в установившемся режиме работы замкнутой СМО при простейших потоках заявок имеют вид:
s0: 0 р0 = 1р1;
sk: λk–1·pk–1 + k+1рk+1 = (λk + k)рk, 1 ≤ k ≤ N0 – 1;
sN0: λN0–1·pN0–1 = N0рN0.
Решением этой системы уравнений с учетом нормировочного равенства p0 + p1 + … + pN0 = 1 будут вероятности того, что в установившемся режиме в СМО имеется k заявок (т.е. k ед. оборудования требуют ремонта):
 ,
где
=
/;
,
где
=
/;

При
небольшом числе каналов n
и числе единиц оборудования N0
рекомендуется использовать рекуррентные
формулы:
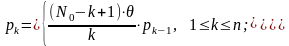
После
выражения по этим формулам через р0
всех рk
для
 вероятность р0
находится из нормировочного равенства
р0
+ р1
+ р2
+ … + рN0
= 1, а затем и вычисляются и остальные
рk.
вероятность р0
находится из нормировочного равенства
р0
+ р1
+ р2
+ … + рN0
= 1, а затем и вычисляются и остальные
рk.
Усредненные параметры функционирования замкнутой СМО рассчитываются по следующим формулам:
среднее число заявок в очереди =
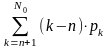 ;
;среднее число заявок в СМО (среднее число единиц неработающего оборудования) =
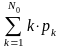 ;
;среднее число свободных каналов обслуживания
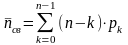 ;
;среднее число занятых каналов обслуживания
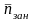 =
п
–
=
п
–
 ;
;доля простаивающих каналов обслуживания /п;
доля неработающих единиц оборудования β = /N0;
доля работающих единиц оборудования γ = 1 – β = 1 – /N0;
среднее время нерабочего состояния конкретного образца оборудования (среднее время пребывания заявки в СМО)
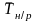 =
=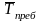 =
=
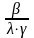 .
.
