Тема: Системы массового обслуживания

1. Основные модели смо

Системы массового обслуживания (СМО) – это системы, предназначенные для выполнения заявок или требований, поступающих на их входы в случайные моменты времени (АТС, АЗС, кассы, станки в цехе, гостиницы, турбазы, парикмахерские, медицинские учреждения, пункты службы быта и т.д.). Рабочие места выполнения заявок называются каналами обслуживания СМО. Среднее число заявок, приходящих в СМО или выходящих из них за единицу времени, называется интенсивностью потока заявок.

СМО делятся на две основные группы:

1) СМО с отказами, в которых заявка, поступающая на вход в момент, когда все обслуживающие каналы заняты, получает отказ (не обслуживается) и покидает систему:

2) СМО с ожиданием, в которых заявка, поступившая на вход, не покидает систему, а ожидает в очереди освобождения какого-либо канала обслуживания:

Частным случаем СМО с ожиданием являются замкнутые СМО, обслуживающие заявки ограниченного числа постоянных клиентов N₀, поэтому интенсивность входящего на вход потока заявок будет уменьшаться с увеличением числа заявок, находящихся в СМО.

Исследуем некоторые простейшие модели СМО в установившемся режиме работы, т.е. когда вероятности возможных состояний СМО под действием простейших потоков заявок, поступающих на их вход и формируемых на их выходе, не изменяются во времени.

2. Характеристики эффективности смо

Важнейшим показателем эффективности функционирования СМО является ее производительная или пропускная способность. Этот показатель определяют несколькими параметрами.

1) Абсолютная номинальная пропускная способность СМО с отказами А₀ – среднее число заявок, которое СМО может обслужить в единицу времени при непрерывной работе всех каналов: для одного канала А₀ = , т.е. по значению  определяется среднее время обслуживания 1-й заявки одним каналом из пропорции:



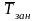 = 1/.

заявок  1 ед. времени

1 заявка 

Для n каналов А₀ = n.

2) Относительная номинальная пропускная способность СМО с отказами ₀ – отношение А₀ к среднему числу заявок, поступающих на вход СМО в единицу времени : ₀ = А₀/. Для одноканальной СМО ₀ = /, параметр  = / называется интенсивностью нагрузки одноканальной СМО.

3) Абсолютная фактическая пропускная способность СМО с отказами А – среднее число заявок, фактически обслуживаемых в единицу времени в СМО, или – среднее число поступающих на вход заявок в единицу времени, которые пропускаются через СМО:

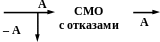
4) Относительная фактическая пропускная способность  = А/ – доля обслуженных в СМО заявок относительно числа поступающих на вход СМО заявок, т.е.  = (число заявок, поступающих на вход в моменты, когда хотя бы один канал свободен, т.е. в благоприятствующие моменты)/(общее число заявок, поступающих на вход СМО) = р_св = 1 – р_отк, где р_св – вероятность того, что поступившая на вход СМО заявка будет обслужена, р_отк – вероятность того, что заявка получит отказ в обслуживании, т.е. вероятность того, что все каналы обслуживания СМО заняты.

5) Относительное время простоя канала  – доля времени простоя канала, равная вероятности того, что этот канал свободен, т.е.  = р_кс.

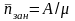
Для многоканальной (n-канальной) системы вводится параметр – среднее число занятых каналов обслуживания, равное отношению числа фактически обслуживаемых заявок в СМО в единицу времени к среднему числу заявок, которое может обслужить один канал, непрерывно работая: 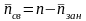 . При этом долевая составляющая времени простоя каждого канала  = р _кс = .

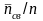Показателями эффективности работы СМО с ожиданием являются среднее число заявок в очереди и среднее время пребывания заявки в СМО.

Все указанные выше показатели зависят от среднего числа заявок, поступающих на вход СМО в единицу времени (), от времени обслуживания заявки одним каналом = 1/ и от числа каналов обслуживания n в СМО.