Численное дифференцирование

Производной функции y=f(x) в точке x₀ называется предел отношения приращения функции y к приращению аргумента x при стремлении x к нулю: .

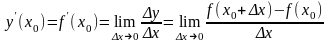Если

• производную от функции в данной точке аналитически найти не удается либо

• вычисление производной слишком громоздко или занимает очень много времени либо

• функция f(x) задана на конечном множестве точек {x_i} (i=0,1,…,n),

то необходимо перейти к численному дифференцированию.

Вычисление производной по определению

Вычисление производной по определению применяется, когда известно аналитическое выражение функции y=f(x).

Пусть функция y=f(x) определена в некоторой окрестности точки x₀ и имеет производную в этой точке, т.е. ,

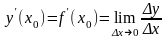Где x=x–x₀ ,

y=f(x₀+x) – f(x₀)

Значение производной функции y=f(x) в точке x₀ получим, рассматривая последовательность ,

где (x)₀ – некоторое начальное приращение аргумента;

a – некоторое число a>1;

n = 0, 1, …

Значение производной примет вид: ,

где 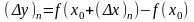, откуда получим: .

Оценим точность приближения.

Пусть функция y=f(x) имеет непрерывную производную до второго порядка включительно в окрестности точки x₀.

По формуле Тейлора ,

откуда ,

где 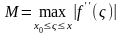– максимальное значение производной на (x, x₀).

Окончательно получим: , где

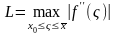
Для достижения заданной степени точности ε при вычислении производной можно использовать неравенство: и, соответственно, последний результат 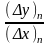принимают в качестве производной функции, вычисленной в точке x с заданной степенью точности.

Блок-схема вычисления производной по определению:

начало

dF:=( f(x+dX)- f(x))/dX

Ввод x,e

конец

dF(x,dX)

dX:=0,1

der1:=dF(x,dX)

Вывод x, der2,e1

конец

+

e1<e

dX:=dX/a

der2:=dF(x,dX)

e1:=|der1-der2|

der1:=der2

Вычисление производной на основе интерполяционного многочлена Лагранжа

Вычисление производной на основе интерполяционного многочлена Лагранжа применяется, когда аналитическое выражение функции y=f(x) не известно, а функция y=f(x) задана таблично.

Пусть функция y=f(x) определена на отрезке и в точках {x_i} (i=0,1,2,…,n) этого отрезка принимает значения y_i=f(x_i).

Разность между соседними значениями аргумента x_i постоянна и является шагом h=x_i– x_i-1 (i=1, …,n) разбиения отрезка на n частей, прием a=x₀ и b=x_n.

Найдем аппроксимации производной первого порядка с помощью значений функций y_i в узловых точках x_i.

Для того чтобы выразить значения производной через значения функции y_i в узлах интерполяции x_i, построим интерполяционный многочлен Лагранжа L_m(x) степени m, удовлетворяющий условиям

L_m(x)= f(x_k)= y_k (k=i, i+1, …, i+m), i+mn

Многочлен Лагранжа L_m(x) интерполирует функцию f(x) на отрезке [x_i, x_i+m]. Дифференцируя многочлен L_m(x), получаем значения производной в точках {x_i} (k=i, i+1, …, i+m).

Если m=2, то график интерполяционного многочлена Лагранжа L₂(x) – парабола, проходящая через три точки (x_i, y_i), (x_i+1, y_i+1) и (x_i+2, y_i+2).

Вычислим первую производную многочлена L₂(x) на отрезке [x_i, x_i+2]:

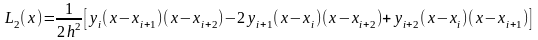
Производная многочлена L₂(x) в точках x_i, x_i+1, x_i+2 является приближением производной функции f(x) в этих точках:

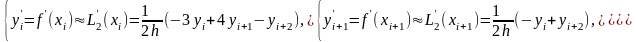(1)

Погрешности при вычислении производных в точках x_i, x_i+1, x_i+2 определяются следующим образом:

(2)

Формулы (2) показывают, что погрешности аппроксимации первой производной с помощью формул (1) имеют один и тот же порядок O(h²), таким образом, можно вычислять производную на отрезке [a,b] в точках {x_i} (i=0,1,2,…,n) при n2 по формулам:

(3)

Полагаем, что значения производных и в точках х, близких к точкам x_i, равны соответствующим значениям и .

Будем считать точку близкой к x_i, если она принадлежит промежутку 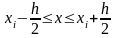. Точки х, близкие к точкам x_i, имеют одно и то же значение параметра

В зависимости от i при n3 используем одну из формул (5).

Программа вычисления производной первого порядка на основе интерполяционного многочлена Лагранжа: