
- •Математические модели и численные методы
- •Структура погрешности при решении задачи на эвм
- •Решение уравнений с одной переменной Постановка задачи
- •Отделение корней
- •I. Графический способ отделения корней
- •II. Отделения корней программным способом.
- •Уточнение корней
- •Метод половинного деления
- •Метод хорд
- •Метод касательных
- •Метод простой итерации
- •Оценка погрешности метода итераций
- •Преобразование к итерационному виду
- •Решение системы линейных алгебраических Постановка задачи
- •Метод Гаусса
- •Метод простой итерации
- •Решение слу методом Зейделя
- •Интерполирование функций Постановка задачи
- •Интерполяционный многочлен Лагранжа
- •Интерполяционный многочлен Ньютона для равноотстоящих узлов
- •Первая интерполяционная формула Ньютона
- •Вторая интерполяционная формула Ньютона
- •Численное дифференцирование
- •Вычисление производной по определению
- •Вычисление производной на основе интерполяционного многочлена Лагранжа
- •Численное интегрирование
- •Формула трапеций
- •Формула Симпсона
- •Приближенное вычисление несобственных интегралов с бесконечными пределами
- •Аппроксимация некоторых несобственных интегралов определенными интегралами с точностью ε.
- •Упрощение подынтегральных функций
- •Приближенное вычисление несобственных интегралов от функции с бесконечным разрывом
- •Численное решение дифференциальных уравнений Основные определения и постановка задачи
- •Метод Эйлера
- •Методы Рунге-Кутта
- •Классический метод Рунге-Кутта
- •Метод наименьших квадратов Постановка задачи
- •Нахождение приближающей функции в виде линейной функции
- •Нахождение приближающей функции в виде других элементарных функций
- •Нахождение приближающей функции в виде квадратичной функции
Интерполяционный многочлен Ньютона для равноотстоящих узлов
Рассмотрим случай, когда h=xi+1 – xi=const (i=0, 1, …).
Рассмотрим конечные разности:
 – конечные разности
1-го порядка – разности между значениями
функции в соседних узлах.
– конечные разности
1-го порядка – разности между значениями
функции в соседних узлах.
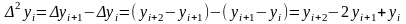 – конечные разности
2-го порядка – разности между конечными
разностями 1-го порядка.
– конечные разности
2-го порядка – разности между конечными
разностями 1-го порядка.
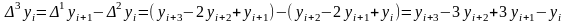 – конечные разности
3-го порядка.
– конечные разности
3-го порядка.
…
 – конечные разности
k-го порядка.
– конечные разности
k-го порядка.
Конечные разности удобно вычислять в таблице:
xi |
yi |
yi |
2 yi |
3 yi |
x0 |
y0 |
y0 |
2 y0 |
3 y0 |
x1 |
y1 |
y1 |
2 y1 |
3 y1 |
x2 |
y2 |
y2 |
2 y2 |
|
x3 |
y3 |
y3 |
|
|
x4 |
y4 |
|
|
|
Первая интерполяционная формула Ньютона
Будем искать интерполяционный многочлен Ньютона в виде многочлена n-ой степени:
Pn(x) = a0+ a1(x-x0) + a2(x-x0)(x-x1) +…+ an(x-x0)…(x-xn-1) (3)
Коэффициенты
a0, a1,
…, an
находятся из условия совпадения значения
исходной функции f(x)
и многочлена Pn(x)
в узлах интерполяции:
 .
.
Пусть
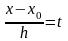 ,
тогда
,
тогда
 ,
соответственно
,
соответственно

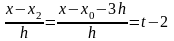
…
Подставив в формулу (3), получим:
 – первая интерполяционная
формула Ньютона.
– первая интерполяционная
формула Ньютона.
Погрешность вычислений оценивается следующим образом:
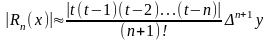
Так
при n=2 
 ,
где
,
где
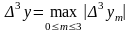
Вторая интерполяционная формула Ньютона
Вторая интерполяционная формула Ньютона применяется, когда значение аргумента ближе к концу отрезка интерполяции (формула для интерполирования назад). Интерполяционный многочлен ищется в виде многочлена n-ой степени:
Pn(x) = a0+ a1(x-xn) + a2(x-xn)(x-xn-1) +…+ an(x-xn)…(x-x1) (4)
Коэффициенты
a0, a1,
…, an
находятся из условия совпадения значения
исходной функции f(x)
и интерполяционного многочлена Pn(x)
в узлах:
 .
.
Подставив
ak
в (4) и перейдя к переменной
 ,
получим вторую интерполяционную формулу
Ньютона:
,
получим вторую интерполяционную формулу
Ньютона:
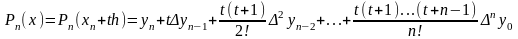 .
.
Погрешность вычислений оценивается следующим образом:
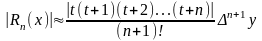 .
.
Рассмотрим задачу субтабулирования (уплотнения таблицы) функции на отрезке. Введем следующие обозначения:
a, b – концы субтабулирования;
H0 – старый шаг таблицы;
H – новый шаг таблицы;
y1, y2, y3 – конечные разности 1-го, 2-го, 3-го порядка;
d – границы погрешности метода.
Для вычисления конечных разностей составляется таблица:
xi |
yi=sin xi |
yi |
2 yi |
3 yi |
0,150 |
0,14944 |
0,00494 |
0,00000 |
-0,00001 |
0,155 |
0,15438 |
0,00494 |
-0,00001 |
0,00001 |
0,160 |
0,15932 |
0,00493 |
0,00000 |
0,00000 |
0,165 |
0,16425 |
0,00493 |
0,00000 |
-0,00001 |
0,170 |
0,16918 |
0,00493 |
-0,00001 |
|
0,175 |
0,17411 |
0,00492 |
|
|
0,180 |
0,17903 |
|
|
|
Блок-схема уплотнения таблиц функций:

