Решение слу методом Зейделя

При решении СЛУ методом простой итерации каждый шаг итерационного процесса состоит в переходе от уже имеющегося приближения значений неизвестных к новому приближению.

Основная идея метода Зейделя состоит в том, что на каждом шаге итерационного процесса при вычислении значений y_i учитываются уже полученные значения y₁, y₂,…,y_i-1.

I. Условие α<1 является достаточным для сходимости итерационного процесса метода Зейделя. Причем метод Зейделя обеспечивает более быструю сходимость, чем метод простой итерации.

II. Рассмотрим практическую схему преобразования исходной СЛУ, гарантирующую сходимость метода Зейделя.

Пусть система записана в матричной форме: Ax=b.

Умножим левую и правую части слева на матрицу A^T: A^TAx= A^T b.

Обозначим : A^TA=C, A^T b=d.

Преобразованная система станет иметь вид: Cx=d. Такую систему называют нормальной:

• матрица C является симметричной;

• все элементы главной диагонали матрицы C положительны.

Нормальную систему легко привести к виду:

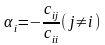, где и .

Вычислительные формулы имеют вид:

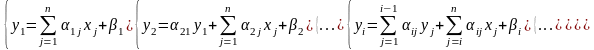
Рассмотрим на примере.

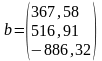
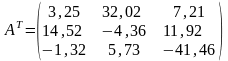
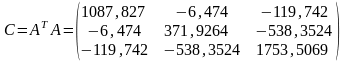
После деления на диагональные элементы получим:

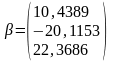
Рассмотрим решение системы трех линейных уравнений с тремя неизвестными методом Зейделя (взяв в качестве метрики, используемой в программе, ).

Интерполирование функций Постановка задачи

Пусть известны значения функции f в некоторых точках:

x	x0	x0	x0	…	(1) x0
f(x)	y0	y0	y0	…	y0

Требуется получить y=f(x) для x[x₀,x_n], где xx_i. При этом аналитическое выражение

• не пригодно ля вычислений либо

• неизвестно.

В этом случае строим приближающую функцию F(x)  f(x), такую что F(x) = f(x) при x=x_i (i=0,1,…,n), т.е.

F(x₀)=y₀, F(x₁)=y₁, …, F(x_n)=y_n (2)

Нахождение приближенной функции называется интерполяцией (интерполированием), точки x₀, x₁, …, x_n узлами интерполяции.

Будим искать функцию F(x) в виде многочлена степени n:

P_n(x) = a₀ xⁿ + a₁ x^n-1 + … + a_n-1 x + a_n

Этот многочлен имеет n+1 коэффициент. Наложим на него n+1 условий (2). Таким образом можно однозначно определить коэффициенты многочлена.

Рассмотрим получившуюся систему уравнений: .

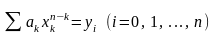Ее определитель (определитель Вандермонда) отличен от нуля:

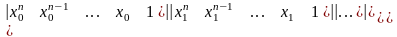
Значит, интерполяционный многочлен P_n(x) для функции f, заданной таблично, существует и единственный. При этом какие-то коэффициенты могут равняться нулю (в том числе и a₀); следовательно, интерполяционный многочлен имеет степень не большую, чем n.

Интерполяционный многочлен Лагранжа

Пусть функция задана таблицей (1). Построим интерполяционный многочлен L_n(x), чья степень не превосходит n, и для которого выполнены условия (2).

L_n(x) ищем в виде L_n(x)= l₀(x)+ l₁(x)+ l₂(x)+…+ l_n(x),

Где l_i(x) – многочлен степени n, причем

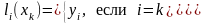
Многочлен l_i(x) составлен следующим образом:

l_i(x)=c_i (x-x₀) (x-x₁)… (x-x_i-1) (x-x_i+1)… (x-x_n), где c_i=const.

Таким образом, получим интерполяционный многочлен Лагранжа:

.

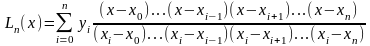Погрешность вычисляется по формуле:

, где

.

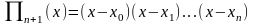Составим интерполяционный многочлен Лагранжа для трех точек:

i	0	1	2
xi	2	4	7
yi	1	-4	5

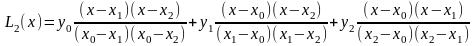
Блок-схема составления интерполяционного многочлена Лагранжа:

Ввод n

i:=1..n

Ввод X[i], Y[i]

Ввод A

F:=0

i:=1..n

L:=1

j:=1..n

Нет

Да

ij

начало

L:=L*Y[i]

F:=F+L

Вывод A, F

Ввод M

M=0

Нет

начало

Да

Программа вычисления значения интерполяционного многочлена Лагранжа: