
- •Математические модели и численные методы
- •Структура погрешности при решении задачи на эвм
- •Решение уравнений с одной переменной Постановка задачи
- •Отделение корней
- •I. Графический способ отделения корней
- •II. Отделения корней программным способом.
- •Уточнение корней
- •Метод половинного деления
- •Метод хорд
- •Метод касательных
- •Метод простой итерации
- •Оценка погрешности метода итераций
- •Преобразование к итерационному виду
- •Решение системы линейных алгебраических Постановка задачи
- •Метод Гаусса
- •Метод простой итерации
- •Решение слу методом Зейделя
- •Интерполирование функций Постановка задачи
- •Интерполяционный многочлен Лагранжа
- •Интерполяционный многочлен Ньютона для равноотстоящих узлов
- •Первая интерполяционная формула Ньютона
- •Вторая интерполяционная формула Ньютона
- •Численное дифференцирование
- •Вычисление производной по определению
- •Вычисление производной на основе интерполяционного многочлена Лагранжа
- •Численное интегрирование
- •Формула трапеций
- •Формула Симпсона
- •Приближенное вычисление несобственных интегралов с бесконечными пределами
- •Аппроксимация некоторых несобственных интегралов определенными интегралами с точностью ε.
- •Упрощение подынтегральных функций
- •Приближенное вычисление несобственных интегралов от функции с бесконечным разрывом
- •Численное решение дифференциальных уравнений Основные определения и постановка задачи
- •Метод Эйлера
- •Методы Рунге-Кутта
- •Классический метод Рунге-Кутта
- •Метод наименьших квадратов Постановка задачи
- •Нахождение приближающей функции в виде линейной функции
- •Нахождение приближающей функции в виде других элементарных функций
- •Нахождение приближающей функции в виде квадратичной функции
Метод простой итерации
Функцию (x,y), определяющую расстояние между точками x и y множества X назовем метрикой, если
(x,y)0
(x,y)=0 x=y
(x,y)= (y,x)
(x,y) (x,z)+ (z,y).
Множество X с введенной метрикой назовем метрическим пространством.
Последовательность
точек метрического пространства
называется фундаментальной,
если
 .
.
Пространство называется полным, если в нем любая фундаментальная последовательность сходится.
Отображение
F
пространства E
в себя называется сжимающим,
если

x – неподвижная точка, если F(x)=x.
Оценка расстояния между неподвижной точкой и приближением x(k) производится следующим образом:
 или
или
 .
.
Таким
образом, чтобы погрешность вычислений
была меньше наперед заданного числа ε,
достаточно потребовать
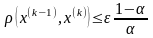 .
.
Рассмотрим 3 типа метрики.
Пусть x(x1,x2,…,xn) и y(y1,y2,…,yn) – две точки n-мерного пространства.
I.
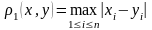 Максимальная из сумм модулей коэффициентов
при неизвестных в правой части системы,
взятых по строкам, должна быть меньше
единицы:
Максимальная из сумм модулей коэффициентов
при неизвестных в правой части системы,
взятых по строкам, должна быть меньше
единицы:

II.
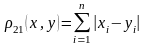 Максимальная из сумм модулей коэффициентов
при неизвестных в правой части системы,
взятых по столбцам, должна быть меньше
единицы:
Максимальная из сумм модулей коэффициентов
при неизвестных в правой части системы,
взятых по столбцам, должна быть меньше
единицы:

III.
 Корень квадратный из суммы квадратов
коэффициентов при неизвестных в правой
части системы, должен быть меньше
единицы:
Корень квадратный из суммы квадратов
коэффициентов при неизвестных в правой
части системы, должен быть меньше
единицы:

СЛУ преобразуется таким образом, чтобы по одной из метрик выполнялось α < 1.

При этом СЛУ задает отображение, которое при α < 1 будет сжимающим. Значит, взяв любую точку в качестве начального приближения, получим последовательность точек, которая будет сходиться к неподвижной точке; это точка и будет решением системы.
Чтобы привести СЛУ к итерационному виду нужно:
с помощью равносильных преобразований привести систему к виду с преобладающими диагональными коэффициентами (по абсолютной величине);
разделить все уравнения на соответствующие диагональные коэффициенты и выразить из каждого уравнения неизвестное с коэффициентом, равным единице.
Если для этой системы α < 1, то система задает сжимающее отображение.
Рассмотрим на примере:
Решим систему трех линейных уравнений с тремя неизвестными.

Преобразуем систему к итерационному виду, для чего поменяем местами 1-ую строку со 2-ой, после чего каждую строку разделим на соответствующие диагональные элементы.

Проверим, будет ли отображение сжимающим:
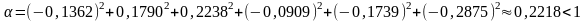
Запишем формулы для решения системы методом итераций:

Программа решения системы трех линейных уравнений с тремя неизвестными методом простой итерации (с использованием евклидовой метрики):
Блок-схема метода простой итерации: |
Ввод
x1,x2,x3,α,ε
начало
p<b
Вывод
x1,x2,x3,N
конец
n:=0
n:=n+1 y1:=… y2:=… y3:=…
+
|






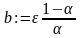

 x1:=y1
x2:=y2
x3:=y3
x1:=y1
x2:=y2
x3:=y3