Нахождение приближающей функции в виде линейной функции

Рассмотрим приближающую функцию в виде F(x,a,b) = ax+b.

Наша задача – отыскать значения параметров a и b.

Рассмотрим функцию 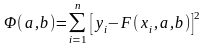или

Задача сводится к отысканию минимума функции Ф(a,b). Используем необходимое условие экстремума: ; .

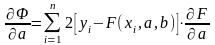
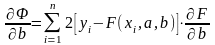
Учитывая, что , , получим систему вида:

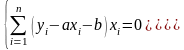
Далее, или

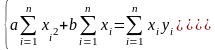
Выразим значения a и b из системы уравнений:

Существует показатель, характеризующий тесноту линейной связи между X и Y. Это (выборочный) коэффициент корреляции. Он вычисляется по формуле:

Значение коэффициента корреляции всегда удовлетворяет соотношению: -1r1. Чем меньше отличается абсолютная величина r от единицы, тем ближе к линии регрессии располагаются экспериментальные точки.

Если коэффициент корреляции равен нулю, то говорят, что переменные X и Y некоррелированы.

Нахождение приближающей функции в виде других элементарных функций

1. Степенная функция: y=a x^m

Прологарифмируем: ln y = ln a + m ln x

Замена: m = A, ln a = B ln y = v ln x = u

Получим функцию v = A u + B

2. Показательная функция: y=a e^mx

Прологарифмируем: ln y = ln a + m x

Замена: m = A, ln a = B ln y = v x = u

Получим функцию v = A u + B

3. Дробно-линейная функция:

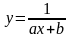
Откуда

Замена: a = A, b = B x = u

Получим функцию v = A u + B

4. Логарифмическая функция: y=a ln x + b

Замена: a = A, b = B y = v ln x = u

Получим функцию v = A u + B

5. Гипербола:

Замена: a = A, b = B y = v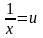

Получим функцию v = A u + B

6. Дробно-рациональная функция:

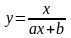
Откуда: ;

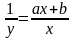Замена: a = B, b = A

Получим функцию v = A u + B

Нахождение приближающей функции в виде квадратичной функции

Рассмотрим приближающую функцию в виде F(x,a,b,с) = ax²+bx+c.

Наша задача – отыскать значения параметров a, b и c.

Рассмотрим функцию .

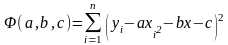
Задача сводится к отысканию минимума функции Ф(a,b,c). Используем необходимое условие экстремума: ; ; .

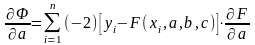
Учитывая, что , , , 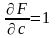получим систему вида:

После дальнейших преобразований

Теперь, поделив уравнения системы на n и введя обозначения:

,

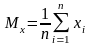
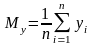
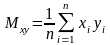
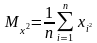
получим систему:

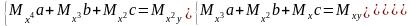
Программа нахождения уравнения регрессии в виде квадратного трехчлена методом наименьших квадратов:

58