Метод Эйлера

В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения, этот метод называется также методом ломаных Эйлера.

Угловой коэффициент касательной к интегральной кривой в точке M₀(x₀,y₀) равен .

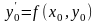Найдем ординату y₁ касательной, соответствующей абсциссе x₁=x₀+h.

Уравнение касательной к кривой в точке M₀ имеет вид 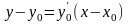или 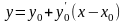, откуда y₁=y₀+hf(x₀,y₀).

Аналогично, угловой коэффициент касательной к интегральной кривой в точке M₁(x₁,y₁) равен 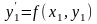. Точку M₂(x₂,y₂) получим соответственно

x₂=x₁+h y₂=y₁+hf(x₁,y₁).

Продолжая вычисления по данной схеме, получим формулы Эйлера для приближенного решения задачи Коши с начальными данными (x₀,y₀) на сетке отрезка [a, b] с шагом h:

x_i=x_i-1+h y_i=y_i-1+hf(x_i-1,y_i-1). (4)

M₄

M₃

Графической иллюстрацией приближенного решения является ломаная, соединяющая последовательно точки M₀, M₁, …,M_m, которую называют ломаной Эйлера.

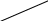
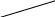
y

M₂

M₁

M₀

O

x

x₀ x₁ x₂ x₃ x₄

Погрешность метода Эйлера можно оценить неравенством

, (5)

которое можно представить в виде d=Ch, где . Таким образом, метод Эйлера имеет первый порядок точности.

Практическую оценку погрешности решения, найденного на сетке с шагом h/2, в точке x_i[a, b] производят с помощью приближенного равенства – правила Рунге:

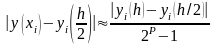(6)

где P – порядок точности численного метода.

Таким образом, оценка полученного результата по правилу Рунге вынуждает проводить вычисления дважды: с шагом h и h/2, причем совпадение десятичных знаков в полученных двумя способами результатах дает основание считать их верными.

Блок-схема решения ДУ методом Эйлера

Методы Рунге-Кутта

Численные методы решения задачи Коши , y(x₀)=y₀ на равномерной сетке {x₀=a, x₁, x₂, …, x_m=b} отрезка [a, b] с шагом являются методами Рунге-Кутта, если, начиная с данных y(x₀)=y₀ решение ведется по следующим рекуррентным формулам:

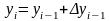; (i=1, 2, …, m) (7)

,

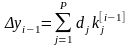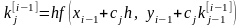
Метод называют методом Рунге-Кутта порядка P, если от имеет P-й порядок точности по шагу h на сетке.

Метод Эйлера можно назвать методом Рунге-Кутта первого порядка.

Метод Рунге-Кутта второго порядка называют методом Эйлера-Коши, если P=2, c₁=0, c₂=1, d₁=d₂=1/2

; (i=1, 2, …, m) (8)

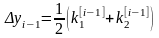
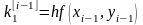
Для практической реализации погрешности решения можно применять правило Рунге, полагая P=2:

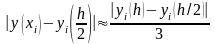
Классический метод Рунге-Кутта

Метод Рунге-Кутта четвертого порядка получаем при

P=4, c₁=0, c₂= c₃=1/2, c₄=1, d₁=d₄=1/6, d₂=d₃=1/3

Расчетные формулы имеют вид:

; (i=1, 2, …, m) (9)

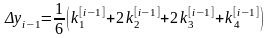
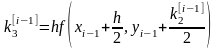
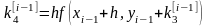
То есть берутся 4 направления и усредняются.

Для практической реализации погрешности решения можно применять правило Рунге, полагая P=4:

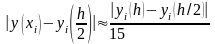
Метод наименьших квадратов Постановка задачи

Пусть данные некоторого эксперимента представлены в виде таблицы:

xi	x1	x2	…	xn
yi	y1	y2	…	yn	(1)

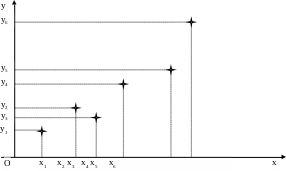Поставим задачу об отыскании аналитической зависимости между x и y, т.е. некоторой формулы y=f(x). При этом потребуем, чтобы график искомой функции изменялся плавно и не слишком уклонялся от экспериментальных данных. Поиск такой зависимости называют «сглаживанием» экспериментальных данных. Формулу y=F(x) – эмпирической формулой или уравнением регрессии y на x.

Предположим, что приближающая функция y=F(x) имеет значения.

xi	x1	x2	…	xn
			…		(2)

Рассматривая совокупности (1) и (2) как координаты двух точек n-мерного пространства, найдем расстояние между ними по евклидовой метрике

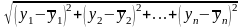
Потребуем, чтобы эта величина была наименьшей. Это равносильно тому, что сумма квадратов должна быть наименьшей:

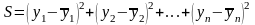или

Тогда задача приближения функции f формулируется следующим образом: для функции f, заданной таблицей, найти функцию F определенного вида так, чтобы сумма квадратов была наименьшей.