Аппроксимация некоторых несобственных интегралов определенными интегралами с точностью ε.

I. 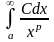, a>0, p>1, C>0

Подынтегральная функция знакоположительна, тогда условие примет вид .

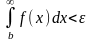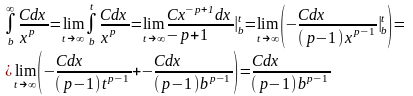
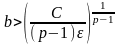Потребуем , откуда получим , причем в качестве верхнего предела интегрирования удобно принять наименьшее целое число, удовлетворяющее неравенству.

Примечание. Если потребовать точность ε/2, неравенство будет иметь вид: .

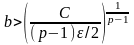II. 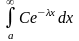, λ>0, C>0.

Подынтегральная функция знакоположительна, тогда условие примет вид .

Потребовав , получим , причем в качестве верхнего предела интегрирования удобно принять наименьшее целое число, удовлетворяющее неравенству.

Примечание. Если потребовать точность ε/2, неравенство будет иметь вид: .

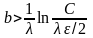Упрощение подынтегральных функций

Несобственный интеграл называют абсолютно сходящимся, если сходится несобственный интеграл .

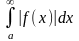Достаточные условия сходимости абсолютно сходящихся интегралов:

• Если 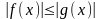для любых значений x на промежутке [a, +) и 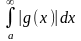сходится, то также сходится.

• Если функции |f(x)| и |g(x)| эквивалентны при x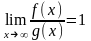 ( ) и несобственный интеграл сходится, то сходится и несобственный интеграл .

Используя достаточные условия сходимости абсолютно сходящихся интегралов можно использовать упрощенные подынтегральные функции вместо заданных.

Приближенное вычисление несобственных интегралов от функции с бесконечным разрывом

Пусть функция f(x) непрерывна на промежутке [a, b) и или не существует.

Если существует предел , то этот предел называют несобственным интегралом функции f(x) на отрезке [a, b] и обозначают, как и определенный интеграл и говорят, что несобственный интеграл функции f(x) сходится на отрезке [a, b].

Аналогично определяется несобственный интеграл в точке a.

Если функция f(x) имеет бесконечный разрыв в точке c отрезка [a, b] и непрерывна при a  x < c и c < x  b, то по определению полагают .

Несобственный интеграл (где f(c)=, a<c<b) называется сходящимся, если существуют оба предела в правой части равенства, и расходящимся, если не существует хотя бы один из них.

Несобственные интегралы с бесконечным разрывом подынтегральной функции на отрезке интегрирования с помощью замены переменной интегрирования преобразуют к несобственным интегралам с бесконечными пределами.

Численное решение дифференциальных уравнений Основные определения и постановка задачи

Дифференциальное уравнение 1-го порядка, разрешенное относительно производной, имеет вид:

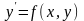(1)

Решением дифференциального уравнения (1) называется функция y(x), подстановка которой в уравнение обращает его в тождество: .

График решения y=y(x) называется интегральной кривой.

Задача Коши для дифференциального уравнения (1) состоит в том, чтобы найти решение дифференциального уравнения (1), удовлетворяющее начальному условию y(x₀)=y₀ (2). Пару чисел (x₀,y₀) называют начальными данными.

Решение задачи Коши называется частным решением дифференциального уравнения (1) при условии (2).

Геометрически задача Коши означает, что требуется найти интегральную кривую y=y(x), проходящую через заданную точку (x₀,y₀).

Теорема о существовании и единственности решения задачи Коши.

Пусть функция f(x,y) – правая часть уравнения - непрерывна вместе со своей частной производной по переменной y 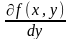в некоторой области D на плоскости. Тогда при любых начальных данных (x₀,y₀)D задача Коши имеет единственное решение y=y(x).

При выполнении условий теоремы через точку (x₀,y₀) на плоскости проходит единственная интегральная кривая.

В классическом анализе разработано немало приемов решения дифференциальных уравнений, однако при решении практических задач эти методы не дают результата. В этом случае прибегают к методам приближенного решения дифференциальных уравнений. В зависимости от формы представления решения выделяют

• аналитические методы (решение в виде аналитического выражения);

• графические методы (решение в виде графика);

• численные методы (решение в виде таблицы).

Численное решение задачи Коши состоит в том, чтобы получить искомое решение y(x) в виде таблицы его приближенных значений аргумента x на некотором отрезке [a, b]:

x₀=a, x₁, x₂, …, x_m=b (3)

Точки (3) называют узловыми, множество этих точек называют сеткой на отрезке [a, b].

Как правило, используют равномерную сетку с шагом h:

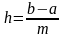
x_i=x₀+ih (i=0, 1, …, m)

Приближенные значения численного решения задачи Коши в узловых точках обозначим y_i.

y_i  y(x_i), где (i=0, 1, …, m)

Начальное условие выполняется точно: y₀ = y(x₀).

Величина погрешности численного решения задачи Коши на сетке отрезка [a, b] оценивается величиной ,

т.е. расстоянием между векторами приближенного решения (y₀, y₁, …,y_m) и точного решения (y(x₀), y(x₁), …,y(x_m)) на сетке по m-норме.