2. Пределы

Пример 2.1. Вычислить .

Решение. Так как , то числитель стремится к числу , а знаменатель – к числу . Значит .

Пример 2.2. Вычислить .

Решение. Числитель и знаменатель дроби неограниченно возрастают при . В этом случае говорят, что имеет место неопределенность вида :

,

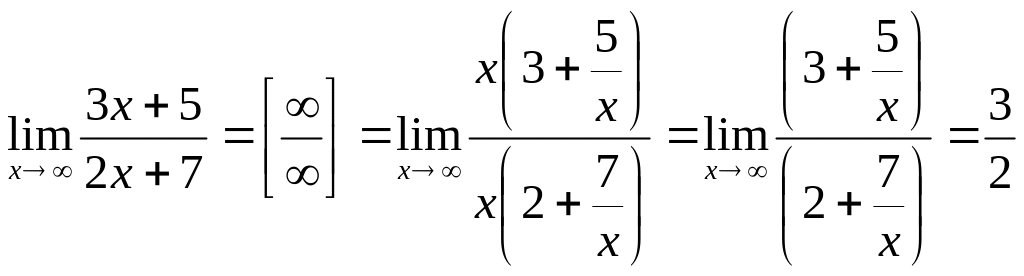так как при каждая из дробей и стремится к нулю.

Пример 2.3. Вычислить .

Решение. Имеет место неопределенность вида . Вынесем за скобки в числителе и знаменатели дроби старшую степень :

.

Пример 2.4. Вычислить .

Решение. .

Пример 2.5. Вычислить .

Решение. .

Пример 2.6. Вычислить .

Решение.

.

Пример 2.7. Вычислить .

Решение. Для раскрытия неопределенности вида умножим числитель и знаменатель на выражение, сопряженное к числителю, получим:

.

Пример 2.8. Вычислить .

Решение. Для раскрытия неопределенности вида удобно предварительно сделать замену , тогда , , при , , а затем полученные многочлены разложить на множители:

.

Пример 2.9. Вычислить .

Решение. Для раскрытия неопределенности вида , как и в примере 2.8, удобно сделать замену: , тогда , при , :

.

Замечание 2.1. При раскрытии в пределах неопределенности вида часто бывает удобно использовать понятие эквивалентности бесконечно малых функций.

Пусть и - бесконечно малые функции при ( ) и , тогда и называются эквивалентными бесконечно малыми при ( ) и обозначают при ( ).

Справедливо следующее утверждение: предел отношения бесконечно малых функций равен пределу отношения эквивалентных бесконечно малых функций, если этот предел существует.

Приведем таблицу основных эквивалентных бесконечно малых функций при :

Таблица 1.

Пример 2.10. Вычислить .

Решение. Для раскрытия неопределенности вида воспользуемся методом замены бесконечно малых эквивалентными (см. таблица 1). При получаем

, ,

откуда находим

.

Пример 2.11. Вычислить .

Решение. Из табл. 1 при : , .

.

Пример 2.12. Вычислить .

Решение. Так как , то непосредственно применить табл. 1 мы не можем. Сделаем предварительно замену: , тогда , при , .

,

при , ,

.

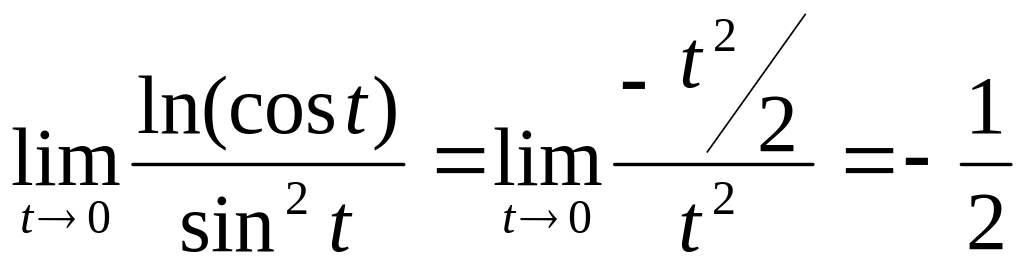Замечание 2.2. При раскрытии в пределах неопределенности вида используют так называемый второй замечательный предел:

Пример 2.13. Вычислить .

Решение. Разделив числитель на знаменатель, выделим целую часть дроби: .

Таким образом, при данная функция представляет собой степень, основание которой стремится к единице, а показатель – к бесконечности (неопределенность вида ). Преобразуя функцию так, чтобы использовать второй замечательный предел, получим:

.

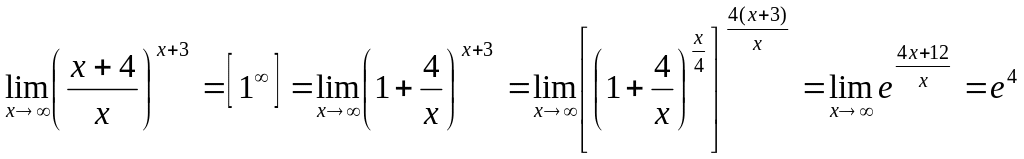Пример 2.14. Вычислить .

Решение.

.

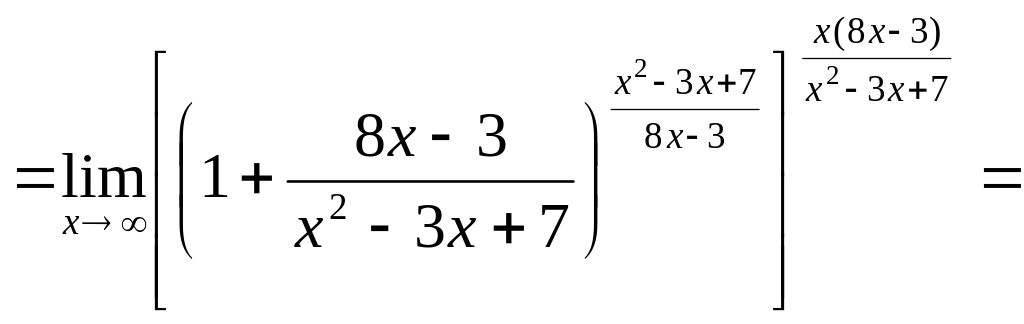
Пример 2.15. Вычислить .

Решение.

,

учитывая, что .

Замечание 2.3. Напомним, что функция с областью определения называется непрерывной в точке , если выполнены следующие условия:

1) функция определена в точке , то есть ;

2) существует ;

3) .

Если в точке нарушено хотя бы одно из условий 1) - 3), то называется точкой разрыва функции . При этом различают следующие случаи:

1) существует, но функция не определена в точке или нарушено условие . В этом случае называется точкой устранимого разрыва.

2) не существует. Но при этом существуют и конечны оба односторонних предела и (очевидно, не равные друг другу), тогда называется точкой конечного скачка.

Точки устранимого разрыва и конечного скачка являются точками разрыва первого рода.

3) в остальных случаях точка называется точкой разрыва второго рода.

Пример 2.16. Исследовать функцию на непрерывность: найти точки разрыва функции и определить их тип. Вычислить , . Построить график функции.

Решение. Рассмотрим точки, в которых функция не определена ( ) и те точки, в которых изменяется аналитическое выражение функции ( ).

1. Рассмотрим . В этой точке функция не определена, следовательно, она является точкой разрыва. Определим ее тип: , ,

так как один из односторонних пределов бесконечен, то - точка разрыва второго рода.

2. . , .

Получаем, что . Следовательно, - точка непрерывности.

3. . , .

Оба односторонних предела и существуют, конечны, но не равны друг другу, следовательно, - точка разрыва первого рода (точка конечного скачка).

4. Вычислим , : , .

5. Построим график функции:

рис. 2.1