Содержание

Предисловие……………………………………………………………………………………….. 3
1.	Элементы линейной алгебры и аналитической геометрии………..……………………...	4
2.	Пределы……………………………………..………………………………………………..	13
3.	Дифференциальное исчисление функции одной переменной…...……………………….	19
Контрольная работа №1…………………………………………………………………………...		24
Контрольная работа №2…………………………………………………………………………...		27
Контрольная работа №3…………………………………………………………………………...		31
Список литературы …...…………………………………………………………………………...		34
Приложения…………...……………………………………………………………………………		38

Пояснительная записка

Цель преподавания математики в вузе – ознакомить студентов с основами математического аппарата, необходимого для решения теоретических и практических задач; привить студентам умение самостоятельно изучать учебную литературу по математике и ее приложениям; развить логическое мышление и повысить общий уровень математической культуры; выработать навыки математического исследования прикладных вопросов и умение перевести задачу на математический язык.

Настоящее пособие для студентов очно-заочной и ускоренной формы обучения всех технических специальностей содержит методические указания и контрольные задания по курсам линейной алгебры и аналитической геометрии, математического анализа.

Перед выполнением контрольной работы студент должен изучить соответствующие разделы курса по учебной литературе, рекомендуемой в данном пособии.

Каждая задача контрольной работы содержит по 30 вариантов. Номер варианта расчетной работы определяется по последним двум цифрам номера зачетной книжки студента и соответствует этим цифрам, если они образуют число от 01 до 30. Если же число больше 30, то номер варианта равен остатку после деления этого числа на тридцать. Если же в остатке получен ноль, тогда ваш вариант 30.

1. Элементы линейной алгебры и аналитической геометрии

Пример 1.1. Заданы матрицы , , . Вычислить:

.

Решение. 1. Вычислим произведение матриц . Найдем размерность матрицы-произведения, если умножение заданных матриц возможно: . Результатом вычисления будет матрица размера .

Вычислим элементы матрицы-произведения, умножая элементы каждой строки матрицы на соответствующие элементы столбцов матрицы следующим образом:

.

2. Найдем матрицу . При транспонировании строки и столбцы матрицы меняются местами с сохранением порядка:

.

3. Умножим матрицу на число 5, при этом каждый элемент матрицы умножается на это число:

.

4. Вычисляем матрицу :

.

Пример 1.2. Решить систему линейных алгебраических уравнений:

1) методом обратной матрицы; 2) методом определителей (методом Крамера); 3) методом Гаусса.

Решение. 1. Метод обратной матрицы.

Введем обозначения:

, , .

Тогда в матричной форме данная система имеет вид: . Умножим слева обе части матричного равенства на обратную матрицу , получим . Так как , то решением системы методом обратной матрицы будет матрица-столбец

.

(1.1)

Найдем матрицу .

Вычислим определитель матрицы А, применяя, например, формулу

.

(1.2)

,

, следовательно, обратная матрица существует.

Вычисляем алгебраические дополнения ко всем элементам матрицы :

, , ,

, , ,

, , .

Составляем матрицу :

.

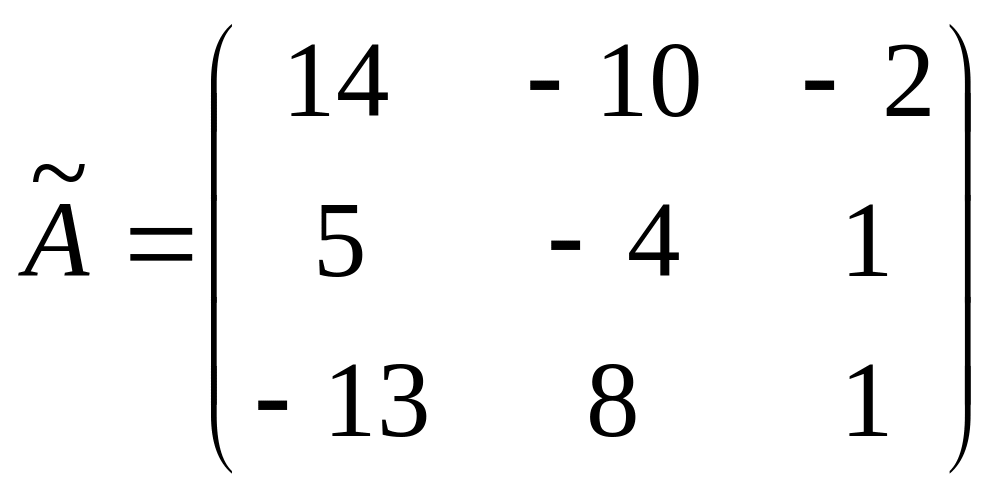Транспонируем матрицу :

.

Находим обратную матрицу:

.

Тогда по формуле (1.1)

,

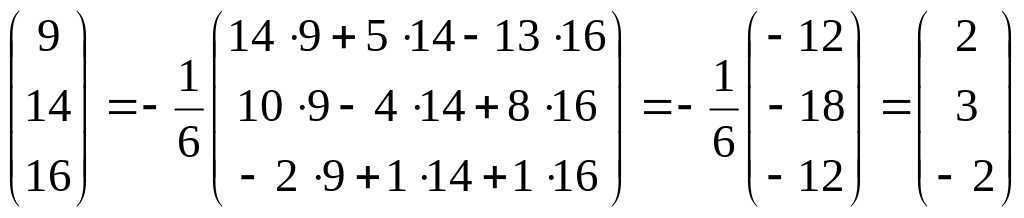то есть решение системы: .