32. Математическое описание линейных непрерывных систем управления в динамическом режиме: частотные характеристики

Частотные характеристики описывают передаточные свойства элементов и систем в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием. Они находят применение в ТАУ, так как реальные возмущения, а, следовательно, и реакции на них элемента или САУ могут быть представлены как сумма гармонических сигналов.

В ТАУ наиболее часто используют следующие частотные характеристики:

- амплитудная частотная характеристика (АЧХ);

- фазовая частотная характеристика (ФЧХ);

- амплитудно-фазовая характеристика (АФХ);

- логарифмические частотные характеристики (ЛЧХ).

Амплитудная частотная характеристика (АЧХ) – зависимость отношения амплитуд выходного и входного сигналов от частоты:

АЧХ показывает, как элемент пропускает сигналы различной частоты.

Фазовая частотная характеристика ФЧХ – зависимость фазового сдвига между входным и выходным сигналами от частоты. ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах: j(w) = j₂(w) - j₁(w),

где j₁(w) -фаза входного сигнала; j₂(w) - фаза выходного сигнала.

Амплитудную и фазовую характеристики можно объединить в одну общую характеристику – амплитудно-фазовую характеристику (АФХ). АФХ представляет собой функцию комплексного переменного jw:

W(jw) = A(w ) e ^{jj (w)} (показательная форма),

г

Рисунок 3.3 – Схема и кривые, поясняющие сущность частотных характеристик:

а - линейный элемент с входным и выходным сигналом; б – соответствие входной и выходной величин

де A(w ) – модуль функции; j (w) – аргумент функции.

Проекции вектора W(jw) на действительную и мнимую оси называют соответственно вещественной (действительной) и мнимой частотными характеристиками (составляющими частотной передаточной функции) и обозначают Re(w ), Jm(w ) соответственно. Это позволяет записать АФХ в алгебраической форме: W(jw) = Re(w ) +j Jm(w ).

АФХ, как и любую комплексную величину, можно также представить в тригонометрической форме:

W(jw) = A(w )cosj (w) + j A(w )sinj (w).

Связь между различными частотными характеристиками следующая:

A(w ) = ç W(jw) ç =

j (w) = arg W(jw) = .

При практических расчетах САУ (без применения электронных вычислительных машин) удобно использовать частотные характеристики, построенные в логарифмической системе координат. Такие характеристики называют логарифмическими. Они имеют меньшую кривизну и поэтому могут быть приближенно заменены ломаными линиями, составленными из нескольких прямолинейных отрезков. Причем, эти отрезки в большинстве случаев удается построить без громоздких вычислений при помощи некоторых простых правил. Частоты, соответствующие точкам стыковки отрезков, называют частотами излома и обозначают w_и. Кроме того, в логарифмической системе координат легко находить характеристики различных соединений элементов, так как умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик.

За единицу измерения по оси частот логарифмических характеристик принимают декаду.

Декада – интервал частот, на котором частота изменяется в 10 раз (интервал частот, заключенный между произвольным значением частоты w_i и его десятикратным значением 10w_i).

Обычно в расчетах используют логарифмическую амплитудную частотную характеристику (ЛАЧХ): L(w) = 20 lg A(w ), ординаты которой измеряют в логарифмических единицах – беллах (Б) или децибеллах (дБ).

Белл – единица измерения мощностей двух сигналов.

L(w)=20 lg A(w)= = 40 дБ.

Наклон отрезков ЛАЧХ определяют в децибелах на декаду (дБ/дек), они имеют положительный и отрицательный наклон, кратный 20 дБ/дек. Масштаб построения ЛАЧХ – логарифмический.

Ось ординат может пересекать ось абсцисс в любом месте (т.к. нуль оси абсцисс лежит слева в минус бесконечности: lg 0 = -¥), таким образом, чтобы охватывался необходимый диапазон частот.

Логарифмическую фазо-частотную характеристику (ЛФЧХ) строят в системе координат с такой же осью абсцисс, что и у ЛАЧХ, а по оси ординат в линейном масштабе угол j(w) в градусах или в радианах. ЛФЧХ обычно строят под ЛАЧХ так, чтобы можно было сопоставить изменение фазы с изменением амплитуды при одинаковых частотах. Масштаб построения ЛФЧХ – полулогарифмический.

На рисунке 3.4 показаны примеры построения частотных характеристик.

Рисунок 3.4 - Частотные характеристики:

а – амплитудная; б – фазовая; в – амплитудно-фазовая; г – логарифмическая АЧХ.

33. Звенья, которые описываются обыкновенными дифференциальными уравнениями первого и второго порядка, получили название типовых динамических звеньев.

Классификацию типовых динамических звеньев удобно осуществить, рассматривая различные частные формы дифференциального уравнения:

.

Значения коэффициентов уравнения

№	Наименование звена	a0	a1	a2	b0	b1	Примечание
1	Безинерционное (пропорциональное)	0	0	1	0	k
2	Инерционное 1-го порядка (апериодическое)	0	T	1	0	k
3	Инерционное 2-го порядка (апериодическое)		T1	1	0	k	T1 ³ 2T2
4	Инерционное 2-го порядка (колебательное)		T1	1	0	k	T1 < 2T2
5	Идеальное интегрирующее	0	1	0	0	k
6	Идеальное дифференцирующее	0	0	1	k	0
7	Реальное дифференцирующее	0	T	1	k	0

К элементарным звеньям можно отнести также следующие звенья:

• консервативное звено с передаточной функцией: ;

• интегрирующее звено с замедлением с передаточной функцией: ;

• изодромное звено с передаточной функцией: ;

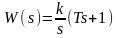• форсирующее звено первого порядка с передаточной функцией: ;

-форсирующее звено 2-го порядка с передаточной функцией: при T₁< 2T₂.

В случае, когда T₁³ 2T₂ данное звено не относится к разряду элементарных и может быть представлено следующей передаточной функцией: .

Для получения частотных характеристик типового звена используются их передаточные функции. Рассмотрим частотные характеристики следующих звеньев:

• Безынерционное (пропорциональное) звено:

частотная передаточная функция:

;

вещественная составляющая частотной передаточной функции:

;

мнимая составляющая частотной передаточной функции: ;

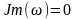модуль частотной передаточной функции (АЧХ): ;

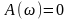аргумент частотной передаточной функции (ФЧХ): ;

ЛАЧХ: ,

проходит параллельно оси абсцисс на расстоянии ;

ЛФЧХ совпадает с осью абсцисс.

- Инерционное 1-го порядка (апериодическое) звено:

частотная передаточная функция:

;

вещественная составляющая частотной передаточной функции: ;

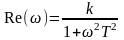мнимая составляющая частотной передаточной функции:

;

модуль частотной передаточной функции (АЧХ): ;

аргумент частотной передаточной функции (ФЧХ):

;

ЛАЧХ: ,

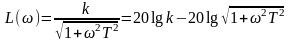причем: L (ω) =20 lg k , при 0 < ωT<< 1,

L (ω) =20 lg k – 20 lg ωT, при Тω >> 1,

для построения ЛАЧХ необходимо найти частоту излома (частоту стыковки двух отрезков) согласно формуле:

;

частота среза для апериодического звена находится по формуле:

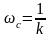
ЛФЧХ: .

• Инерционное 2-го порядка (апериодическое) звено:

частотная передаточная функция:

или ;

модуль частотной передаточной функции (АЧХ):

или ;

аргумент частотной передаточной функции (ФЧХ):

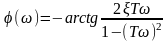
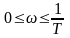
, при

, при ;

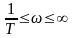Результирующая ЛАЧХ звена: , где L₁(w), L₂ (w) – ЛАЧХ двух последовательно соединенных апериодических звеньев 1-го порядка;

ЛФЧХ отличается от ФЧХ только логарифмической шкалой оси частот.

• Инерционное 2-го порядка (колебательное) звено:

частотная передаточная функция:

;

вещественная составляющая частотной передаточной функции:

;

мнимая составляющая частотной передаточной функции:

; модуль частотной передаточной функции (АЧХ):

; аргумент частотной передаточной функции (ФЧХ):

;

ЛАЧХ: 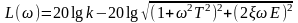; ЛФЧХ отличается от ФЧХ только логарифмической шкалой оси частот.

• Идеальное интегрирующее звено:

частотная передаточная функция:

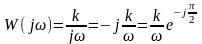; вещественная составляющая частотной передаточной функции:

; мнимая составляющая частотной передаточной функции: ;

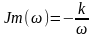модуль частотной передаточной функции (АЧХ): ; аргумент частотной передаточной функции (ФЧХ): ;

ЛАЧХ: представляет собой прямую линию, которая пересекает ось абсцисс в точке (частота среза) и имеет наклон -20 дБ/дек;

ЛФЧХ не зависит от частоты и проходит параллельно оси абсцисс на расстоянии .

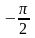• Идеальное дифференцирующее звено:

частотная передаточная функция:

;

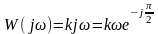вещественная составляющая частотной передаточной функции:

;

мнимая составляющая частотной передаточной функции: ;

модуль частотной передаточной функции (АЧХ): ;

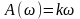аргумент частотной передаточной функции (ФЧХ): ;

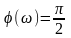ЛАЧХ: ,

представляет собой прямую линию, которая пересекает ось абсцисс при частоте среза дифференцирующего звена:

и имеет наклон +20 дБ/дек;

ЛФЧХ: не зависит от частоты и проходит параллельно оси абсцисс на расстоянии .

• Реальное дифференцирующее звено (дифференцирующее звено с замедлением):

частотная передаточная функция:

;

аргумент частотной передаточной функции (ФЧХ): ;

ЛАЧХ: ,

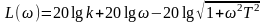представляет собой ломанную кривую, состоящую из двух отрезков, первый отрезок пересекает ось абсцисс при частоте среза (3.45) и имеет наклон +20 дБ/дек, при частоте излома (3.44) ЛАЧХ становиться параллельной оси абсцисс и располагается на высоте ;

ЛФЧХ отличается от ФЧХ только логарифмической шкалой оси частот.

• Звено запаздывания:

частотная передаточная функция:

;

вещественная составляющая частотной передаточной функции:

;

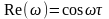мнимая составляющая частотной передаточной функции:

;

модуль частотной передаточной функции (АЧХ): ;

аргумент частотной передаточной функции (ФЧХ): ;

ЛАЧХ: ;

ЛФЧХ отличается от ФЧХ только логарифмической шкалой оси частот.

• Консервативное звено:

частотная передаточная функция:

,

график этой функции при изменении частоты w от нуля до плюс бесконечности имеет вид двух полупрямых: при изменении частоты w от 0 до резонансной частоты 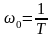первая полупрямая начинается на вещественной положительной полуоси в точке и идет в бесконечность в положительном направлении; вторая полупрямая начинается в минус бесконечности при и идет по отрицательной вещественной полуоси в начало координат при ;

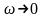вещественная составляющая частотной передаточной функции:

;

мнимая составляющая частотной передаточной функции: ;

АЧХ имеет разрыв на частоте 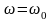имеет разрыв, соответствующий бесконечному возрастанию амплитуды;

ФЧХ при частоте скачком изменяет фазу от 0 до -p;