31. Математическое описание линейных непрерывных систем управления в динамическом режиме: временные характеристики

Различают следующие формы динамических характеристик:

- обыкновенное дифференциальное уравнение;

- временные характеристики;

- передаточная функция;

- частотные характеристики.

Временные характеристики. Дифференциальное уравнение не дает наглядного представления о динамических свойствах элемента, но такое представление дает функция y(t), т.е. решение этого уравнения. Однако одно и то же дифференциальное уравнение может иметь множество решений, зависящих от начальных условий и характера входного воздействия x(t), что неудобно при сопоставлении динамических свойств различных элементов. Поэтому было решено характеризовать эти свойства элемента только одним решением дифференциального уравнения, полученным при нулевых начальных условиях и одном из типовых воздействий: единичном ступенчатом, дельта-функции, гармоническом, линейном.

Под начальными условиями понимают значение выходной величины и всех ее производных в момент времени t = t₀ при условии, что до этого времени внешние воздействия отсутствовали.

Начальные условия называются нулевыми, если выполняется условие: .

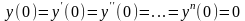С

тупенчатое воздействие – воздействие, которое мгновенно возрастает от нуля до некоторого значения и далее остается постоянным

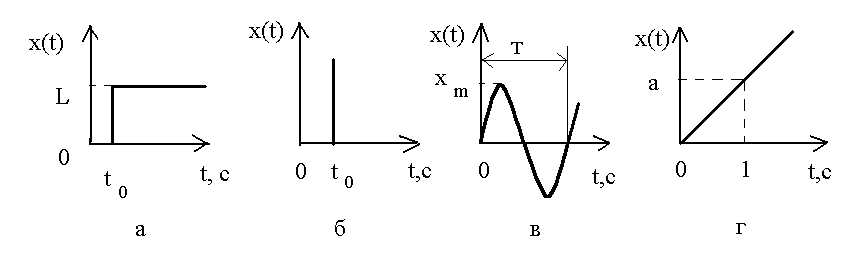
С Рисунок 3.2 – Типовые воздействия: а – ступенчатое; б – импульсное; в – гармоническое; г – линейное тупенчатому воздействию соответствует функция:

0 при t< 0;

x(t) =

L при t ³ 0.

При анализе и расчете систем удобно использовать ступенчатое воздействие, у которого величина L = 1. Его называют единичным ступенчатым воздействием и обозначают 1(t). Математическое выражение, описывающее единичное ступенчатое воздействие, имеет вид:

0 при t< 0;

1(t) =

1 при t ³ 0.

Ступенчатое воздействие чаще всего используют при исследованиях систем стабилизации параметров, так как эти воздействия наиболее близки к реальным входным (задающим и возмущающим) воздействиям систем стабилизации. Реакция звена на единичную ступенчатую функцию при нулевых начальных условиях называется переходной функцией, которую принято обозначать h(t). Графическое изображение переходной функции называют переходной характеристикой.

Импульсное воздействие – одиночный импульс прямоугольной формы (рисунок 3.2б), имеющий достаточно большую высоту и малую длительность (по сравнению с инерционностью испытываемой системы) с площадью а₀. При математическом анализе САУ используют единичное импульсное воздействие описываемое дельта-функцией Дирака:

0 при t< 0;

d (t) =

¥ при t> 0, причем

Последние два выражения позволяют рассматривать дельта-функцию, как импульс, имеющий бесконечно большую высоту, бесконечно малую длительность и единичную площадь. Дельта-функцию можно определить также как производную единичного ступенчатого воздействия: Нормальная реакция звена на импульсную функцию называется импульсной переходной функцией или весовой функцией (функцией веса), которую принято обозначать v(t). Графическое изображение переходной функции называют импульсной переходной характеристикой.

Гармоническое воздействие – сигнал синусоидальной формы, описываемый функцией (рисунок 3.2в): x(t) = x_m sinw t , (-¥ < t < ¥ ), (3.9)

где x_m – амплитуда сигнала; w = 2p / Т – круговая частота; Т – период сигнала. Гармонический сигнал, начинающий действовать в момент времени t = 0, описывают при помощи единичной ступенчатой функции:

x(t) = 1(t) x_m sinw t , (0 £ t < ¥ ). (3.10)

Линейное воздействие – воздействие, описываемое функцией:

x(t) = 1(t) а₁ t , (0 £ t < ¥ ), (рисунок 3.2г). Коэффициент а₁ характеризует скорость нарастания воздействия x(t).