Текст 2 Основні поняття

В ектором називається напрямлений відрізок. Якщо початок вектора знаходиться в точці А, кінець – у точці В, то вектор позначається символом АВ або АВ. Початок вектора називають також точкою його прикладання. Вектор іноді позначається однією малою буквою жирного шрифту а, b і т.ін., або такою самою буквою світлого шрифту з рискою вгорі а, b і т.п.

М одулем вектора а називається його довжина, він позначається через |а| або просто а. Модуль вектора – скалярна негативна величина.

Нулъ-вектором (або нульовим вектором) називається вектор, початок і кінець якого збігаються. Нуль-вектор позначається символом 0. Його модуль дорівнює 0, а напрям не визначений.

С D

К L N М

Одиничним називається вектор, довжина якого дорівнює одиниці.

В ектори, які лежать на паралельних або на одній прямій, називаються колінеарними (вектори CD і MN, KL і MN, CD і KL).

К олінеарні вектори, що мають однакові напрями і довжини, називаються рівними (ВС = AD) Якщо вектори АВ і CD мають протилежні напрями, то вони не рівні АВ ≠ CD ; АВ = CD.

З азначимо, що ОМ₁ ≠ ОМ₂, де М₁, М₂ – дві різні точки кола з радіусом R і центром О, оскільки вектори ОМ₁ і ОМ₂ мають різні напрями.

В ектори, які мають протилежні напрямки та рівні за довжиною, називаються протилежними (вектор АВ і CD). Вектор, протилежний вектору а, позначається –а.

Вектори, які лежать у паралельних площинах (або в одній площині), називаються компланарними.

Вектор, точка прикладання якого може бути вибрана довільно, називається вільним.

Завдання 7 За допомогою таблиці дайте визначення різних векторів.

Назва вектора	Модуль	Напрям	Інші властивості
Нульовий	0	не визначений
Одиничний	1
Колінеарні: - рівні - протилежні	рівні рівні	однакові протилежні	на | |-их прямих або на одній прямій
Компланарні			у | |-их площинах (або в одній)
Вільний			початок довільний

Завдання 8 Виконайте такі дії, поясніть їх.

1 Нарисуйте нульовий вектор, позначте модуль і напрям.

2 Нарисуйте паралелограм ABCD, позначте напрям векторів: АВ, СВ, AD, DC. Охарактеризуйте дані вектори.

3 Нарисуйте декартові координати в просторі. Які це вектори?

Завдання 9 Прочитайте текст 3, порівняйте його з текстом 1. Скажіть, про які операції з векторами ви прочитали в тексті 1, а яка інформація нова? Доповніть план тексту 1.

Текст 3 Лінійні операції над векторами

Лінійними операціями над векторами називають додавання, віднімання, множення вектора на число.

1 Складання векторів. Сумою векторів а і b називається третій вектор с, початок якого збігається з початком вектора а, а кінець – з кінцем вектора b за умови, що вектор b відкладений з кінця вектора а. Вектор с виходить за правилом трикутника або паралелограма (рис. 1).

Р ис. 1

Аналогічно визначається сума трьох і більше векторів. Сумою п векторів a₁, a₂ ..., а_п називається вектор, початок якого збігається з початком першого вектора a₁, кінець – з кінцем останнього а_п за умови, що кожний наступний вектор а_к+1 відкладений з кінця попереднього а_к (k = 1,2 ..., n – 1).

Сума векторів має властивість комутативності (рис. 2):

а + b = b + а

і властивістю сполучності (асоціативності):

(а + b) + с = а + (b + с).

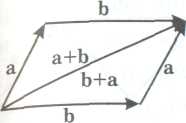
Рис. 2

С ума трьох некомпланарних векторів а, b, с визначається і за правилом паралелепіпеда: сума а + b + с рівна вектору OD, де OD – діагональ паралелепіпеда, побудованого на векторах ОА = а, ОВ = b, ОС = с, відкладених з однієї точки (рис. 3).

D

b B

А

О

С

Рис. 3

З визначення суми випливає, що а + 0 = а; а + (–а) = 0.

2 Віднімання векторів. Різницею а – b двох векторів а і b називається такий вектор d, який у сумі з вектором b дає вектор а:

а – b = d, якщо b + d = а.

Щоб отримати різницю а – b двох векторів а і b, необхідно відкласти їх з однієї точки і з’єднати кінець другого вектора з кінцем першого (рис. 4).

1 Різниця а – b дорівнює сумі двох векторів а і (–b), де (–b) – вектор, протилежний вектору b (рис. 5), тобто а – b = а + (-b).

Рис. 4

Рис. 5

В ектори – діагоналі паралелограма ОАСВ (рис. 6), побудова-ного на векторах ОА= а, ОВ = b, є відповідно сумою і різницею цих векторів.

С

А

Рис. 6

3 Множення векторів. Добутком вектора а на число а називається вектор b = α а, що задовольняє умовам:

1) b = α а;

2) b і а однаково напрямлені, якщо а > 0;

3) b і а мають протилежні напрями, якщо а < 0.

а

2,5а

-3а

Очевидно, b = 0, якщо α = 0 або а = 0.

Добуток вектора на число має такі властивості:

1 α(βа)= (αβ) а; α (а + b) = αa + αb; (α +β) а = αa + βа.

2 Добуток числа на суму векторів дорівнює сумі добутків числа на кожний вектор.

3 Добуток вектора на суму чисел дорівнює сумі добутків вектора на кожне число.

Завдання 10 Відповідайте на запитання.

1 Що є сумою векторів АВ і ВС?

2 Як знайти суму трьох і більше векторів? Нарисуйте.

3 Як називається такий спосіб побудови?

4 Які властивості має сума векторів?

5 Як знайти суму трьох некомпланарних векторів?

Завдання 11 Закінчіть речення, використовуючи інформацію прочитаних текстів.

1 Вектор характеризується ... .

2 Вектор, початок і кінець якого збігаються, називається ... .

3 Довжина одиничного вектора дорівнює ... .

4 Колінеарні вектори лежать на ... .

5 Рівні колінеарні вектори мають ... .

6 Якщо вектори мають протилежні напрями, вони ... .

7 Компланарні вектори лежать у ... .

8 Вектор, початок якого вибраний довільно ... .

9 Сума векторів визначається за правилом ... .

10 Різницю двох векторів можна отримати, якщо відкласти їх ... .

11 Вектором називається ... .

12 Операції складання і множення векторів схож і… .