2. Адаптивный эквалайзер.

Применение эквалайзера в модемах позволяет значительно повысить эффективность использования полосы при передаче данных по телефонным и радиоканалам.

Существует несколько алгоритмов синтеза адаптивных эквалайзеров [1]. В лабораторной работе рассматриваются рекуррентные алгоритмы минимальных квадратов для адаптивного выравнивания - алгоритм Калмана и алгоритм кратчайшего спуска (градиентный метод). В основе обоих алгоритмов лежит метод наименьших квадратов. Рекуррентные процедуры более просты и требуют меньший объем памяти при реализации на цифровой схемотехнической базе.

Рассматриваемый эквалайзер построен на базе трансверсального фильтра (линейный эквалайзер) с числом линий задержек N (см. рис 3).

Генератор обучающей последовательности.

Детектор

1

2

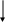
выход

Алгоритм оценивания коэффициентов

Рис. 3. Структурная схема эквалайзера.

На вход эквалайзера поступают отсчеты , ( ) дискретизированного по времени комплексного сигнала (см. формулу (1)).

, - оператор математического ожидания. Сначала ключ находится в положении «1». На этом этапе происходит обучение по известной информационной последовательности, т.е. оцениваются коэффициенты трансверсального фильтра так, чтобы разность между сигналом на выходе фильтра , где , -вектор комплексных коэффициентов, «Т» - знак транспонирования, и тестовой последовательностью свести к минимуму.

(2)

После периода обучения, когда коэффициенты эквалайзера сошлись к своим оптимальным значениям, ключ переходит в положении «2». На этом этапе сигнал - продетектированные решения, которые являются выходом эквалайзера. Они достаточно надежны, поэтому их можно дальше использовать для адаптации коэффициентов.

1. Калмановский алгоритм оценивания коэффициентов эквалайзера.

Алгоритм оценивания коэффициентов синтезирован с помощью теории рекуррентной линейной фильтрации.

Предположим, что каждая компонента вектора является медленно меняющимся случайным процессом. Тогда ее можно аппроксимировать авторегрессией первого порядка , где - матрица размером , , - единичная матрица размером ,«*»- знак комплексно сопряженной величины.

Таким образом, получим модель:

(3)

Пусть .

Требуется по входной последовательности и тестовому сигналу синтезировать алгоритм оценивания вектора коэффициентов эквалайзера по критерию (2) минимума средней квадратической ошибки (СКО). Полученные оценки должны быть асимптотически несмещенными: , асимптотически эффективными: и состоятельными: . Здесь - оператор математического ожидания, - вероятность.

Используя модель (3) поставленную задачу можно решить модифицированным методом наименьших квадратов (МНК), который основывается на минимизации функционала Тихонова А.Н.:

(4)

Здесь - евклидова норма, , - скалярное произведение.

Минимизируя (4), получим выражение для оценок комплексного вектора коэффициентов эквалайзера:

(5)

,

.

- ковариационная матрица ошибок экстраполяции, - ковариационная матрица ошибок фильтрации.

Начальные условия: - из априорных сведений, - единичная матрица размером .

Рис. 4. Структурная схема алгоритма (5) .

Достоинство алгоритма: быстрая сходимость.

Недостатки: 1)сложность; 2) чувствительность к шуму, который накапливается при рекуррентных операциях и может вызвать нестабильность алгоритма.