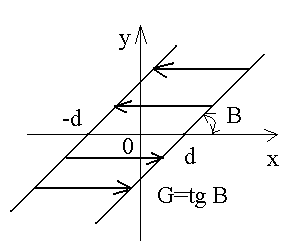- •Конспект лекций по дисциплине «Основы теории автоматического управления» для студентов специальности 050713 – Транспорт, транспортная техника и технологии
- •Тема 1. Введение
- •Функциональная структура (схема) – структура (схема), отражающая функции (целевые назначения) отдельных частей асу.
- •Тема 2. Основные задачи теории автоматического управления
- •Тема 3. Математические модели сау
- •С Рисунок 3.2 – Типовые воздействия: а – ступенчатое; б – импульсное; в – гармоническое; г – линейное тупенчатому воздействию соответствует функция:
- •Лачх имеет разрыв на частоте излома ; лфчх на частоте излома имеет скачок фазы от 0 до -p.
- •Вид афчх на комплексной плоскости приведен на рисунке 3.9 а.
- •Тема 4. Методы исследования линейных сау
- •Р исунок 4.3 - Схема четырехполюсника с нелинейным резистором
- •Тема 5. Методы исследования нелинейных сау
- •Тема 6. Устойчивость систем автоматического управления
- •Тема 7. Качество систем автоматического управления
- •Тема 8. Случайные воздействия в линейных сау.
- •Тема 9. Задачи оптимального управления
- •Тема 10. Современные тенденции развития систем управления
Р исунок 4.3 - Схема четырехполюсника с нелинейным резистором
В функцию Ф (дифференциальное уравнение) входят также величины, называемые параметрами. Они связывают между собой аргументы (y(t), y¢(t),… y(n)(t); x(t),…x(m)(t), t) и характеризуют свойства элемента с количественной стороны. Например, параметрами являются масса тела, активное сопротивление, индуктивность и емкость проводника и т. д.
Большинство реальных элементов описываются нелинейными дифференциальными уравнениями, что значительно усложняет последующий анализ АСУ. Поэтому стремятся перейти от нелинейных к линейным уравнениям вида:
(4.4)
Для всех реальных элементов выполняется условие m £ n .
Коэффициенты a0, a1…an и b0, b1…bm в уравнении (4.4) называются параметрами. Иногда параметры изменяются во времени, тогда элемент называют нестационарным или с переменными параметрами. Таковым, например, является четырехполюсник, схема которого приведена на рисунке 4.3. Однако в дальнейших рассуждениях будем рассматривать только элементы с постоянными параметрами.
Если при составлении линейного дифференциального уравнения осуществлялась линеаризация статической характеристики элемента, то оно справедливо лишь для окрестности точки линеаризации и может записываться в отклонениях переменных x и y от значений x0 и y0 :
Dy = y - y0 ; (4.5)
Dx = x - x0 . (4.6)
Тогда с учетом этих обозначений выражение принимает вид:
Dy = k Dx, (4.7)
где k = y¢(x0) – передаточный коэффициент элемента, характеризующий его передаточные свойства в статическом режиме.
Однако, с целью упрощения записи, отклонения переменных в линеаризованном уравнении будем обозначать теми же символами, что и в исходном нелинейном уравнении, но без символа D .
Важнейшим практическим достоинством линейного уравнения (4.4) является возможность применения принципа наложения, согласно которому изменение выходной величины y(t), возникающее при действии на элемент нескольких входных сигналов xi(t), равно сумме изменений выходных величин yi(t), вызываемых каждым сигналом xi(t) в отдельности (рисунок 4.4).

Рисунок 4.4 - Иллюстрация принципа наложения
Контрольные вопросы:
1. По каким признакам классифицируются системы автоматического управления?
2. Какая САУ называется непрерывной?
3. Какая САУ называется дискретной?
4. Как составляются обыкновенные дифференциальные уравнения?
Тема 5. Методы исследования нелинейных сау
Цель лекции: уяснить особенности, отличающие нелинейные системы от линейных; изучить основные виды нелинейностей; изучить некоторые частные способы решения нелинейных дифференциальных уравнений; изучить основные методы определения устойчивости нелинейных систем.
План лекции:
1. Понятие нелинейных САУ. Классификация нелинейностей.
2. Устойчивость нелинейных систем. Методы исследования нелинейных систем.
1. Нелинейными называются системы автоматического управления, динамика движения которых описывается нелинейными дифференциальными уравнениями. Если хотя бы одно звено САУ имеет нелинейную статическую характеристику, то вся САУ является нелинейной. Большинство нелинейных САУ можно представить в виде последовательного соединения двух частей системы: линейной и нелинейной как показано на рисунке 5.1. Wл(s) - передаточная функция линейных элементов системы; Wнл(s) –передаточная функция нелинейных элементов системы; Wf(s) – предаточная функция линейного объекта управления по возмущению.
Рисунок 5.1 –
Структурная схема нелинейной САУ.
Почти все реальные элементы САУ нелинейны. Нелинейности можно разделить на две группы: гладкие несущественные и существенные.
К гладким несущественным нелинейностям относятся такие нелинейности, на которых при малом диапазоне изменения аргумента можно выбрать участки, близкие к линейным, и заменить их линейными участками. Такие САУ на выбранном диапазоне изменения аргумента можно считать линейными, и проводить их анализ как анализ линейных САУ.
Существенные нелинейности обычно являются: разрывными или неоднозначными функциями или функциями, имеющими изломы. Преобразование любого входного воздействия для такой характеристики всегда нелинейно. Существенные нелинейности весьма разнообразны. Основные виды таких нелинейностей приведены в таблице 5.1.
Указанные в таблице примеры звеньев ни в коей мере не претендуют на полноту. Такие нелинейные характеристики могут иметь элементы и другой физической природы. Нелинейные САУ характеризуются более сложными и разнообразными динамическими процессами по сравнению с линейными САУ. Характер движения нелинейных САУ зависит от начальных условий. В нелинейных САУ возможен без каких-либо внешних возмущений новый по сравнению с линейными САУ вид установившегося движения – автоколебания, то есть устойчивые колебания с определенной амплитудой и частотой, зависящих от конструктивных особенностей САУ. Если на вход нелинейной САУ подать периодическое возмущение, то в ней могут наблюдаться особые случаи резонанса, который может происходить на частоте, равной доле частоты входного воздействия. Возможен и ряд других особенностей движения нелинейных САУ.
Таблица 5.1 – Основные виды нелинейностей второй группы.
Название нелинейности |
Вид статической характеристики |
y = f (t) |
Примеры реальных устройств |
Зона насыщения
|
|
|
Электрические усилители |
Зона нечувствительности |
|
x <- d
x > d |
Механические усилители |
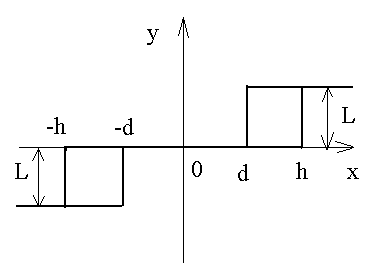
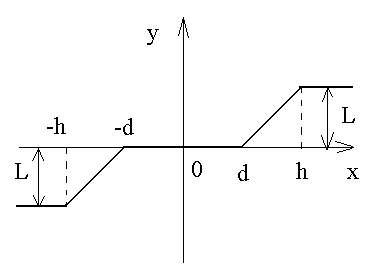
Зона нечувствительности и зона насыщения |
|
, x < - h
h < x < -d ,
d < x < h , x > h |
Гидравлические и пневматические усилители |
Идеальное двухпозиционное реле |
|
, x > 0 , x < 0 |
Идеализированная характеристика двухпозиционных электрических приборов |
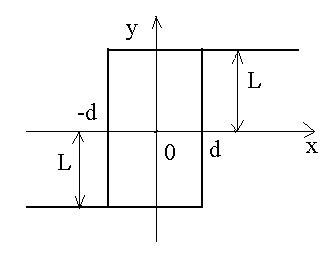
Идеальное реле с зоной нечувствительности |
|
, x < - d , , x > d
|
Идеализированная характеристика трехпозиционных электромагнитных приборов |
Двухпозиционное реле |
|
, x < d при х1t > 0
, x < - d при х1t < 0
|
Реле. Реальные двухпозиционные переключающие элементы |
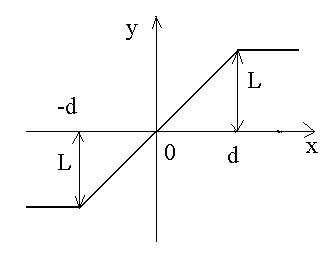
Трехпозиционное реле |
|
y = L , x < h y = 0, -d < x < h y = - L , x < -d при x1t > 0
y = L , x > d y = 0, -h < x < d y = - L , x < -h при x1t < 0
|
Реальные трехпозиционные переключающие элементы |
Люфт, зазор или сухое трение
|
|
y = G(x - d), x1t > 0 y = G(x – d) x1t < 0
|
Различные механические передачи с люфтами, зазорами и сухим трением |
2. Вопрос об устойчивости нелинейных САУ нельзя решить так же просто как в линейных САУ. Нелинейная САУ может быть устойчива в малом (при незначительных начальных возмущениях) и неустойчива в большом (если начальные условия превышают некоторые определенные граничные значения). Нелинейная САУ может иметь область устойчивости равновесного состояния с постоянным значением регулируемой величины и быть асимптотически устойчивой. Она может иметь одну или несколько областей устойчивых автоколебаний. Нелинейная САУ неустойчива в малом и имеет устойчивые автоколебания в большом. Нелинейные САУ могут иметь области неустойчивости.
Поведение нелинейных САУ описывается нелинейными дифференциальными уравнениями. Общих методов решения этих уравнений нет, и для анализа работы нелинейных САУ при разработке и проектировании используют некоторые частные способы решения нелинейных уравнений: метод фазового портрета, метод гармонической линеаризации, метод припасовывания, статистической линеаризации и т.д.
Контрольные вопросы:
1. Какие системы автоматического управления называются нелинейными?
2. Какими дифференциальными уравнениями описывается движение нелинейных САУ?
3. Какие Вы знаете виды нелинейностей?
3. Назовите основные виды существенных нелинейностей и приведите примеры реальных устройств, имеющих существенно нелинейные характеристики.
4. От чего зависит характер движения нелинейных САУ?
5. Когда могут возникнуть автоколебания в нелинейной системе?
6. Как решается вопрос об устойчивости нелинейных САУ?
7. Когда нелинейная САУ устойчива в малом и неустойчива в большом?
8. Какими свойствами могут обладать нелинейные САУ?
9. Какие способы решения нелинейных дифференциальных уравнений используют при разработке и проектировании? Перечислите их.

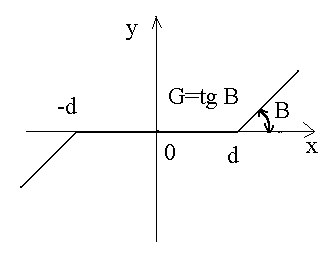


 ,
x
> d
,
x
> d ,
x
> -d
,
x
> -d