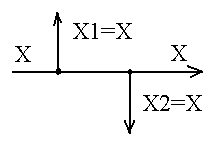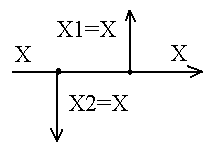Лачх имеет разрыв на частоте излома ; лфчх на частоте излома имеет скачок фазы от 0 до -p.

• Интегрирующее звено с замедлением (реальное интегрирующее звено):

частотная передаточная функция:

; (3.83)

модуль частотной передаточной функции (АЧХ): ; (3.84)

аргумент частотной передаточной функции (ФЧХ): ; (3.85)

ЛАЧХ: , (3.86)

представляет собой ломанную кривую, состоящую из двух отрезков, первый из которых пересекает ось абсцисс при частоте среза (4.46) и имеет наклон +20 дБ/дек, при частоте излома (4.21) ЛАЧХ ломается на - 20 дБ/дек и имеет наклон равный - 40 дБ/дек;

ЛФЧХ отличается от ФЧХ только логарифмической шкалой оси частот.

• Изодромное звено:

частотная передаточная функция:

; (3.87)

модуль частотной передаточной функции (АЧХ): ; (3.88)

ЛАЧХ (3.89)

представляет собой ломанную кривую, состоящую из двух отрезков, первый из которых пересекает ось абсцисс при частоте среза (3.69) и имеет наклон -20 дБ/дек, при частоте излома (3.44) ЛАЧХ ломается на + 20 дБ/дек и становится параллельной оси частот;

ЛФЧХ отличается от ФЧХ только логарифмической шкалой оси частот.

Аналогичным образом можно найти частотные характеристики и других звеньев.

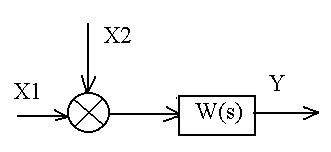
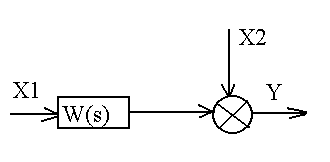
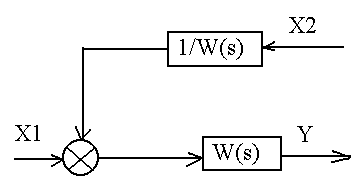
5. Для анализа САУ используются их структурные схемы. Схема системы управления, в которой функциональные элементы представлены типовыми динамическими звеньями, называется структурной схемой. На структурных схемах все воздействия следует представлять в виде лапласовых изображений. Для упрощения (свертывания) сложных структурных схем применяют правила их преобразования. Основным условием преобразования структурных схем в эквивалентную является неизменность динамических характеристик системы.

Три главных правила относятся к трем типовым соединениям звеньев:

- последовательному;

- параллельному;

- параллельно-встречному.

Если эти соединения состоят из элементов направленного действия, то каждое такое соединение может быть заменено одним элементом, статические и динамические характеристики которого эквивалентны свойствам соединения.

Рассмотрим эти типовые соединения звеньев при известности их передаточных функций.

·

Рисунок 3.4 – Последовательное соединение динамических звеньев.

Последовательное соединение звеньев - это такое соединение двух или более звеньев, при котором выходная величина предыдущего звена является входной величиной последующего (рисунок 3.4).

Найдем передаточную функцию W(s) звена, эквивалентного последовательному соединению звеньев. Искомая передаточная функция эквивалентного звена:

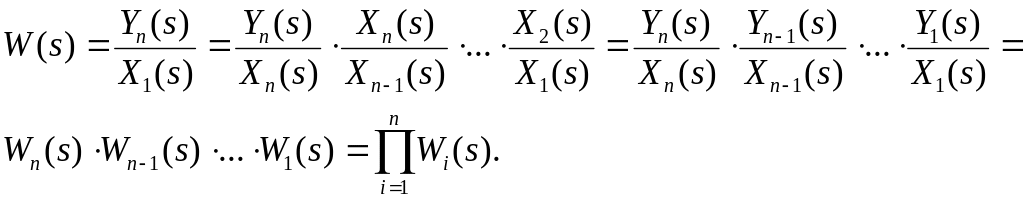_(3.90)

Частотная передаточная функция последовательного соединения звеньев: . (3.91)

Из этого выражения вытекает, что при последовательном соединении звеньев их АЧХ перемножаются, а ФЧХ складываются.

При использовании логарифмических частотных характеристик, то для последовательного соединения: , (3.92)

то есть ЛАЧХ последовательного соединения звеньев равна сумме их ЛАЧХ.

Статическая характеристика в этом случае будет линейной, а угол ее наклона к оси абсцисс a = arctg k. (3.93)

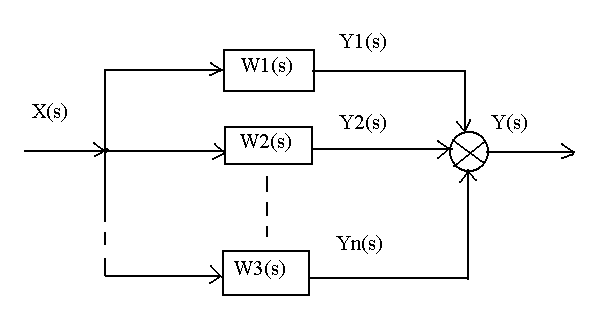
· Параллельное соединение звеньев – это такое соединение двух или более звеньев, при котором входная величина всех звеньев одна и та же, а их выходные величины складываются (рисунок 3.5).

Найдем передаточную функцию W(s) звена, эквивалентного параллельному соединению звеньев. Искомая передаточная функция эквивалентного звена:

_(3.94)

Ч

астотная передаточная функция параллельного соединения: . (3.95)

В

Рисунок 3.5 – Параллельное соединение динамических звеньев.

ектор АФХ параллельного соединения для каждой частоты равен сумме векторов АФХ звеньев, входящих в соединение, следовательно, проекция вектора соединения на вещественную и мнимую оси соответственно равны сумме проекций отдельных векторов, значит:

(3.96)

на основании этого можно записать:

(3.97)

Для построения статической характеристики параллельного соединения звеньев, статические характеристики которых известны, необходимо построить эти характеристики в одной системе координат и сложить их ординаты для одинаковых значений входной величины.

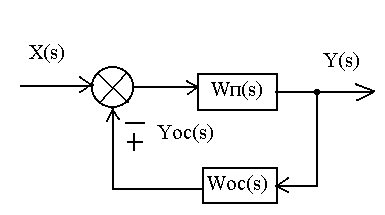
• Параллельно-встречное соединение звеньев (встречно-параллельное соединение звеньев, соединение звеньев с обратной связью) - это такое соединение звеньев, при котором выходная величина одного звена подается обратно на его вход через другое звено (рисунок 3.6).

Найдем передаточную функцию W(s) звена, эквивалентного параллельно-встречному соединению звеньев. Выходная величина параллельно встречного соединения звеньев может быть найдена исходя из следующих выражений:

(3.98)

где f_п , f_ос – статические характеристики звеньев прямой цепи и цепи обратной связи соответственно.

П

осле решения этой системы уравнений относительно у и представления звеньев их передаточными функциями получим:

, (3.99)

г

Рисунок 3.6 – Параллельно-встречное соединение динамических звеньев.

де W_п(s) и W_ос (s) – передаточные функции соответственно прямой цепи и цепи обратной связи параллельно-встречного соединения звеньев.

После деления обеих частей равенства на X(s) получаем:

, (3.100)

учитывая, что: получаем передаточную функцию параллельно-встречного соединения: _{. (3.101)}

При отрицательной обратной связи в знаменателе передаточной функции ставится знак плюс, при положительной обратной связи – знак минус.

Частотная передаточная функция параллельно-встречного соединения звеньев: . _(3.102)

В случае, когда W_ос(s) = 1 обратная связь называется единичной, а передаточная функция параллельно-встречного соединения звеньев с единичной обратной связью будет иметь вид: . (3.103)

Частотная передаточная функция параллельно-встречного соединения звеньев с единичной обратной связью: . (3.104)

Для частотных функций параллельно-встречного соединения звеньев нет простых аналитических выражений связи с частотными функциями входящих в соединение звеньев, то на практике для отыскания вещественной и мнимой составляющих АФХ соединения, имеющих практическое значение, пользуются специальными номограммами.

С помощью рассмотренных правил удается преобразовать (упростить) к простейшему виду любую структурную схему, не содержащую перекрестных связей между звеньями. Если же схема многоконтурная и содержит перекрестные связи, то эти правила можно применять лишь после устранения этих перекрестных связей. Для устранения перекрестных связей следует использовать ряд вспомогательных правил преобразований структурных схем, которые приведены в таблице 3.3.

Таблица 3.3 – Вспомогательные правила преобразования структурных схем.

№	Операция	Исходная схема	Преобразованная схема
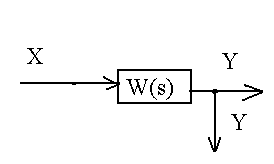
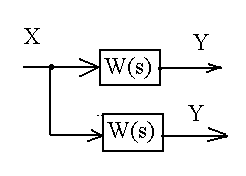
1	Перестановка узлов разветвления
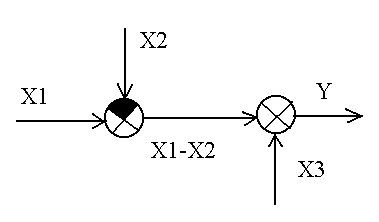
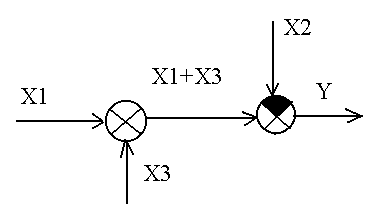
2	Перестановка сумматоров
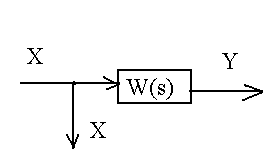
3	Перенос узла разветвления через звено вперед
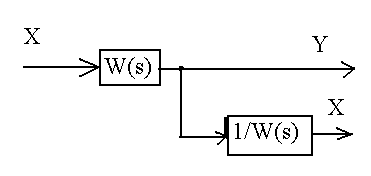
4	Перенос узла разветвления через звено назад

5	Перенос сумматора через звено вперед
6	Перенос сумматора через звено назад

Могут также использоваться и другие частные правила преобразования структурных схем.

6 . Для элемента САУ (четырехполюсника), схема и параметры которого приведены на рисунке 3.7, найдем следующие статические и динамические характеристики: дифференциальное уравнение, переходную функцию, передаточную функцию, передаточный коэффициент, частотные (амплитудно-фазовую, амплитудную, фазовую, логарифмическую амплитудную) характеристики.

Рисунок 3.7 - Схема и параметры элемента

Составление дифференциального уравнения элемента.

В соответствии с законами линейных электрических цепей записываем следующие уравнения: r i+ u_c = e ; (3.105)

(3.106)

Подставляя значение тока i из выражения (3.106) в уравнение (3.105) получаем дифференциальное уравнение: (3.107)

Подставляя параметры r и c четырехполюсника уравнение (3.107) получаем искомое дифференциальное уравнение элемента: (3.108)

Нахождение переходной функции элемента.

Полагаем входной сигнал четырехполюсника равным единичному ступенчатому воздействию e = 1(t). Тогда его выходной сигнал будет равен переходной функции u_c = h(t).

Учитывая сказанное в уравнении (3.108), приводим его к виду:

1(t). (3.109)

Вынужденную составляющую переходной функции находим из уравнения (3.109), полагая в нем производную dh(t) /dt)= 0, h_в(t) = 1. (3.110)

Составляем характеристическое уравнение, соответствующее дифференциальному уравнению (3.109): 0,1p + 1 = 0. (3.111)

Корень характеристического уравнения p = -10.

Свободную составляющую переходной функции находим по выражению h_с(t) = при n = 1 и p₁ =-10, получаем: (3.112)

Находим переходную функцию, суммируя ее вынужденную (3.110) и свободную (3.112) составляющие, h(t) = h_в(t) + h_с(t) = (3.113)

Из уравнения (3.113) при нулевых начальных условиях (h(0) = 0 ) определяем коэффициент C₁ = -1.

Подставляя значение этого коэффициента в выражение (3.113), находим искомую переходную функцию элемента: (3.114)

График переходной функции элемента приведен на рисунке 3.8.

Рисунок 3.8 - График переходной функции элемента

Нахождение передаточной функции элемента.

В дифференциальном уравнении (3.108) степени полиномов правой и левой частей соответственно m = 0 и n = 1. Тогда коэффициенты этого уравнения b₀ = 1; a₀ = 0,1; a₁ = 1.

При этих коэффициентах по выражению находим искомую передаточную функцию элемента: (3.115)

Нахождение передаточного коэффициента элемента.

Искомый передаточный коэффициент элемента находим по выражению при b₀ = 1 и a₁ = 1 равен: (3.116)

или из выражения (3.115) при p=0 равен: (3.117)

Определение частотных характеристик элемента.

Амплитудно-фазовую частотную характеристику (АФЧХ) элемента находим из выражения W(j) = W(p)_{p = j} путем подстановки в него передаточной функции (3.115) при p = jw :

(3.118)