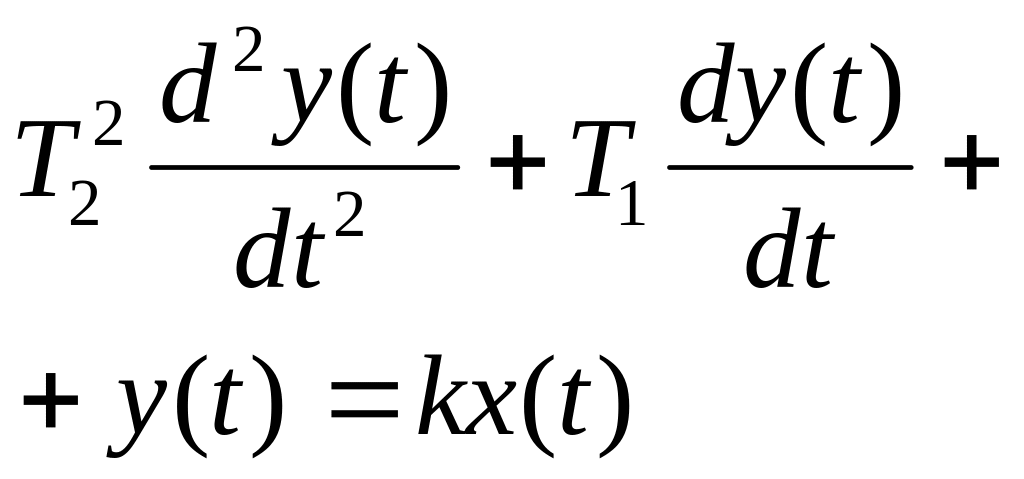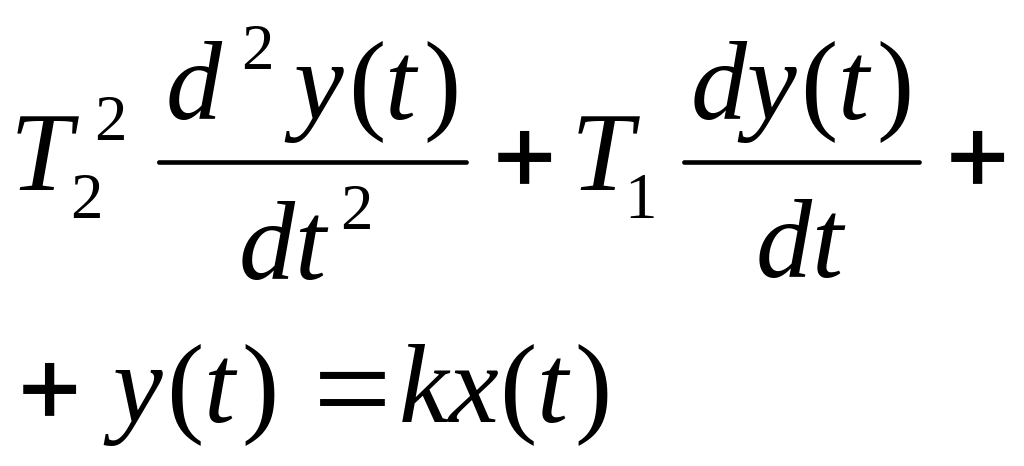С Рисунок 3.2 – Типовые воздействия: а – ступенчатое; б – импульсное; в – гармоническое; г – линейное тупенчатому воздействию соответствует функция:

0 при t< 0;

x(t) = (3.6)

L при t ³ 0.

При анализе и расчете систем удобно использовать ступенчатое воздействие, у которого величина L = 1. Его называют единичным ступенчатым воздействием и обозначают 1(t). Математическое выражение, описывающее единичное ступенчатое воздействие, имеет вид:

0 при t< 0;

1(t) = (3.7)

1 при t ³ 0.

Ступенчатое воздействие чаще всего используют при исследованиях систем стабилизации параметров, так как эти воздействия наиболее близки к реальным входным (задающим и возмущающим) воздействиям систем стабилизации. Реакция звена на единичную ступенчатую функцию при нулевых начальных условиях называется переходной функцией, которую принято обозначать h(t). Графическое изображение переходной функции называют переходной характеристикой.

Импульсное воздействие – одиночный импульс прямоугольной формы (рисунок 3.2б), имеющий достаточно большую высоту и малую длительность (по сравнению с инерционностью испытываемой системы) с площадью а₀. При математическом анализе САУ используют единичное импульсное воздействие описываемое дельта-функцией Дирака:

0 при t< 0;

d (t) = (3.8)

¥ при t> 0, причем

Последние два выражения позволяют рассматривать дельта-функцию, как импульс, имеющий бесконечно большую высоту, бесконечно малую длительность и единичную площадь. Дельта-функцию можно определить также как производную единичного ступенчатого воздействия: Нормальная реакция звена на импульсную функцию называется импульсной переходной функцией или весовой функцией (функцией веса), которую принято обозначать v(t). Графическое изображение переходной функции называют импульсной переходной характеристикой.

Гармоническое воздействие – сигнал синусоидальной формы, описываемый функцией (рисунок 3.2в): x(t) = x_m sinw t , (-¥ < t < ¥ ), (3.9)

где x_m – амплитуда сигнала; w = 2p / Т – круговая частота; Т – период сигнала. Гармонический сигнал, начинающий действовать в момент времени t = 0, описывают при помощи единичной ступенчатой функции:

x(t) = 1(t) x_m sinw t , (0 £ t < ¥ ). (3.10)

Линейное воздействие – воздействие, описываемое функцией:

x(t) = 1(t) а₁ t , (0 £ t < ¥ ), (рисунок 3.2г). Коэффициент а₁ характеризует скорость нарастания воздействия x(t).

• Передаточная функция.

Наиболее распространенным методом описания и анализа САУ является операционный метод (метод операционного исчисления), в основе которого лежит прямое интегральное преобразование Лапласа для непрерывных функций: F(s) = Z { f(t) } = f(t) e^-pt dt . (3.11)

Это преобразование устанавливает соответствие между функцией действительной переменной t и функцией комплексного переменного s = s + jw. Функцию f(t), входящую в интеграл Лапласа, называют оригиналом, а результат интегрирования – функцию F(s) – изображением функции f(t) по Лапласу. Преобразование выполнимо лишь для функций, которые равны нулю при t< 0. Формально это условие в ТАУ обеспечивается умножением функции f(t) на единичную ступенчатую функцию 1(t) или выбором начала отсчета времени с момента, до которого f(t) = 0.

Наиболее важными свойствами преобразования Лапласа при нулевых начальных условиях являются:

Z { f¢(t) } = sF(s); Z { f (t)dt } = F(s) /s. (3.12)

Операционный метод в ТАУ получил широкое распространение, так как с его помощью определяют так называемую передаточную функцию, которая является самой компактной формой описания динамических свойств элементов и систем.

Применяя прямое преобразование Лапласа к дифференциальному уравнению, получим алгебраическое уравнение: D(s)Y(s) = K(s)X(s), (3.13)

где D(s) = a₀ sⁿ + a₁ s^n-1 +…+ a_n - собственный оператор (характеристический полином (многочлен)),

K(s) = b₀ s^m + b₁ s^m-1 +…+ b_m - входной оператор.

Введем понятие передаточной функции.

Передаточная функция – отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях:

_(3.14)

Тогда с учетом уравнения (3.4) и обозначений выражение для передаточной функции принимает вид: (3.15)

Значение переменной s, при которой передаточная функция W(s) обращается в бесконечность, называется полюсом передаточной функции. Очевидно, что полюсами являются корни собственного оператора D(s).

Значение переменной s, при которой передаточная функция W(s) обращается в нуль, называется нулем передаточной функции. Очевидно, что нулями являются корни входного оператора K(s).

Если коэффициент a₀ ¹ 0, то передаточная функция не имеет нулевого полюса (s = 0), характеризуемый ей элемент называют астатическим и передаточная функция этого элемента при s = 0 (t = ¥) равна передаточному коэффициенту

При чисто мнимом значении комплексного переменного s (s = jw) передаточная функция называется частотной передаточной функцией и обозначается W(jw).

По виду частотных характеристик все элементы делятся на две группы:

- минимально-фазовые;

- неминимально-фазовые.

Минимально-фазовый элемент – элемент, у которого все полюсы и нули передаточной функции W(s) имеют отрицательные действительные части.

• Частотные характеристики.

Частотные характеристики описывают передаточные свойства элементов и систем в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием. Они находят применение в ТАУ, так как реальные возмущения, а, следовательно, и реакции на них элемента или САУ могут быть представлены как сумма гармонических сигналов.

Рассмотрим сущность и разновидности частотных характеристик. Пусть на вход линейного элемента (рисунок 3.3а) в момент времени t = 0 подано гармоническое воздействие с частотой w: x(t) = x_m sinw t. По завершении переход

ного процесса установится режим вынужденных колебаний и выходная величина y(t) будет изменяться по тому же закону, что и входная x(t), но в общем случае с другой амплитудой y_m и с фазовым сдвигом j по оси времени относительно входного сигнала (рисунок 3.3б): y(t) = y_m sin(w t + j ). Проведя аналогичный опыт, но при другой частоте w, можно увидеть, что амплитуда y_m и фазовый сдвиг j изменились, т.е. они зависят от частоты. Можно убедиться также, что для другого элемента зависимости параметров y_m и j от частоты w иные. Поэтому такие зависимости могут служить характеристиками динамических свойств элементов.

В ТАУ наиболее часто используют следующие частотные характеристики:

- амплитудная частотная характеристика (АЧХ);

- фазовая частотная характеристика (ФЧХ);

- амплитудно-фазовая характеристика (АФХ);

- логарифмические частотные характеристики (ЛЧХ).

Амплитудная частотная характеристика (АЧХ) – зависимость отношения амплитуд выходного и входного сигналов от частоты: (3.16)

АЧХ показывает, как элемент пропускает сигналы различной частоты.

Фазовая частотная характеристика ФЧХ – зависимость фазового сдвига между входным и выходным сигналами от частоты. ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах: j(w) = j₂(w) - j₁(w), (3.17)

где j₁(w) -фаза входного сигнала; j₂(w) - фаза выходного сигнала.

Рисунок 3.3 – Схема и кривые, поясняющие сущность частотных характеристик:

а - линейный элемент с входным и выходным сигналом; б – соответствие входной и выходной величин

Амплитудную и фазовую характеристики можно объединить в одну общую характеристику – амплитудно-фазовую характеристику (АФХ). АФХ представляет собой функцию комплексного переменного jw:

W(jw) = A(w ) e ^{jj (w)} (показательная форма), (3.18)

где A(w ) – модуль функции; j (w) – аргумент функции.

Каждому фиксированному значению частоты w_i соответствует комплексное число W( jw_i ), которое на комплексной плоскости можно изобразить вектором, имеющим длину A(w_i ) и угол поворота j (w_i ). Отрицательные значения j(w), соответствующие отставанию выходного сигнала от входного, принято отсчитывать по часовой стрелке от положительного направления действительной оси. При изменении частоты от нуля до бесконечности вектор W(jw) поворачивается вокруг начала координат, при этом одновременно изменяется длина вектора. Кривая, которую при этом опишет конец вектора, и есть АФХ. Каждой точке характеристики соответствует определенное значение частоты.

Проекции вектора W(jw) на действительную и мнимую оси называют соответственно вещественной (действительной) и мнимой частотными характеристиками (составляющими частотной передаточной функции) и обозначают Re(w ), Jm(w ) соответственно. Это позволяет записать АФХ в алгебраической форме: W(jw) = Re(w ) +j Jm(w ). (3.19)

АФХ, как и любую комплексную величину, можно также представить в тригонометрической форме:

W(jw) = A(w )cosj (w) + j A(w )sinj (w). (3.20)

Связь между различными частотными характеристиками следующая:

A(w ) = ç W(jw) ç = (3.21)

j (w) = arg W(jw) = . (3.22)

Минимально-фазовые элементы дают минимальный фазовый сдвиг j (w) по сравнению с любыми другими элементами, имеющими такую же амплитудную характеристику A(w), но у которой действительная часть хотя бы одного полюса или нуля положительна. Минимально-фазовые элементы обладают важным для практических расчетов свойством: их частотная передаточная функция полностью определяется одной из трех составляющих - A(w), Re(w) и Jm(w). Это существенно упрощает задачи анализа и синтеза минимально-фазовых систем.

При практических расчетах САУ (без применения электронных вычислительных машин) удобно использовать частотные характеристики, построенные в логарифмической системе координат. Такие характеристики называют логарифмическими. Они имеют меньшую кривизну и поэтому могут быть приближенно заменены ломаными линиями, составленными из нескольких прямолинейных отрезков. Причем, эти отрезки в большинстве случаев удается построить без громоздких вычислений при помощи некоторых простых правил. Частоты, соответствующие точкам стыковки отрезков, называют частотами излома и обозначают w_и. Кроме того, в логарифмической системе координат легко находить характеристики различных соединений элементов, так как умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик.

За единицу измерения по оси частот логарифмических характеристик принимают декаду.

Декада – интервал частот, на котором частота изменяется в 10 раз (интервал частот, заключенный между произвольным значением частоты w_i и его десятикратным значением 10w_i).

Обычно в расчетах используют логарифмическую амплитудную частотную характеристику (ЛАЧХ): L(w) = 20 lg A(w ), (3.23)

ординаты которой измеряют в логарифмических единицах – беллах (Б) или децибеллах (дБ).

Белл – единица измерения мощностей двух сигналов.

Если мощность одного сигнала больше (меньше) мощности другого сигнала в 10 раз, то эти мощности отличаются на 1 Б, (lg 10 = 1). Так как мощность гармонического сигнала пропорциональна квадрату его амплитуды, то при применении этой единицы для измерения отношения амплитуд перед логарифмом появляется множитель 2. Например, если на некоторой частоте A(w ) = 100, то это означает, что мощности входного и выходного сигналов отличаются в 100² раз, т.е. на 2 lg 100 = 4 Б или на 40 дБ, соответственно и L(w)=20 lg A(w)= = 40 дБ.

Наклон отрезков ЛАЧХ определяют в децибелах на декаду (дБ/дек), они имеют положительный и отрицательный наклон, кратный 20 дБ/дек. Масштаб построения ЛАЧХ – логарифмический.

Ось ординат может пересекать ось абсцисс в любом месте (т.к. нуль оси абсцисс лежит слева в минус бесконечности: lg 0 = -¥), таким образом, чтобы охватывался необходимый диапазон частот.

Логарифмическую фазо-частотную характеристику (ЛФЧХ) строят в системе координат с такой же осью абсцисс, что и у ЛАЧХ, а по оси ординат в линейном масштабе угол j(w) в градусах или в радианах. ЛФЧХ обычно строят под ЛАЧХ так, чтобы можно было сопоставить изменение фазы с изменением амплитуды при одинаковых частотах. Масштаб построения ЛФЧХ – полулогарифмический.

На рисунке 3.4 показаны примеры построения частотных характеристик.

Рисунок 3.4 - Частотные характеристики:

а – амплитудная; б – фазовая; в – амплитудно-фазовая; г – логарифмическая АЧХ.

4. Функциональные элементы, используемые в САУ, могут иметь самые различные конструктивное выполнение и принципы действия. Однако общность математических выражений, связывающих входные и выходные величины различных функциональных элементов, позволяет выделить ограниченное число так называемых типовых звеньев. Каждому типовому звену соответствует определенное математическое соотношение между входной и выходной величинами. Если это соотношение является элементарным (например, дифференцирование, умножение на постоянный коэффициент), то и звено называется элементарным.

Звенья, которые описываются обыкновенными дифференциальными уравнениями первого и второго порядка, получили название типовых динамических звеньев.

Типовые динамические звенья являются основными составными частями схем САУ, поэтому знание их характеристик существенно облегчает анализ таких систем.

Классификацию типовых динамических звеньев удобно осуществить, рассматривая различные частные формы дифференциального уравнения:

. (3.24)

Значения коэффициентов этого уравнения и названия для наиболее часто применяемых звеньев приведены в таблице 3.1.

Таблица 3.1 – Значения коэффициентов уравнения (3.24).

№	Наименование звена	a0	a1	a2	b0	b1	Примечание
1	Безинерционное (пропорциональное)	0	0	1	0	k
2	Инерционное 1-го порядка (апериодическое)	0	T	1	0	k
3	Инерционное 2-го порядка (апериодическое)		T1	1	0	k	T1 ³ 2T2
4	Инерционное 2-го порядка (колебательное)		T1	1	0	k	T1 < 2T2
5	Идеальное интегрирующее	0	1	0	0	k
6	Идеальное дифференцирующее	0	0	1	k	0
7	Реальное дифференцирующее	0	T	1	k	0

Передаточные и переходные функции для наиболее часто применяемых звеньев приведены в таблице 3.2.

К элементарным звеньям можно отнести также следующие звенья:

• консервативное звено с передаточной функцией:

; (3.25)

• интегрирующее звено с замедлением с передаточной функцией: ; (3.26)

• изодромное звено с передаточной функцией: ; (3.27)

• форсирующее звено первого порядка с передаточной функцией: ; (3.28)

-форсирующее звено 2-го порядка с передаточной функцией: при T₁< 2T₂. (3.29)

В случае, когда T₁³ 2T₂ данное звено не относится к разряду элементарных и может быть представлено следующей передаточной функцией: . (3.30)

Таблица 3.2 – Передаточные и переходные функции наиболее часто применяемых звеньев.

№	Наименование звена и описывающее его уравнение	Передаточная функция	Переходная функция
1	Безынерционное (пропорциональное)
2	Инерционное 1-го порядка (апериодическое)
3	Инерционное 2-го порядка (апериодическое) T1 ³ 2T2	T1 ³ 2T2 или или 1<< x< ¥	где ; .

4	Инерционное 2-го порядка (колебательное) T1 < 2T2	T1 < 2T2 или x > 1	, где ; ; .
5	Идеальное интегрирующее
6	Идеальное дифференцирующее

7	Реальное дифференцирующее
8	Звено запаздывания

Для получения частотных характеристик типового звена используются их передаточные функции. Рассмотрим частотные характеристики следующих звеньев:

• Безынерционное (пропорциональное) звено:

частотная передаточная функция:

_{; (3.31)}

вещественная составляющая частотной передаточной функции:

; (3.32)

мнимая составляющая частотной передаточной функции: ; (3.33)

модуль частотной передаточной функции (АЧХ): ; (3.34)

аргумент частотной передаточной функции (ФЧХ): ; (3.35)

ЛАЧХ: , (3.36)

проходит параллельно оси абсцисс на расстоянии ;

ЛФЧХ совпадает с осью абсцисс.

- Инерционное 1-го порядка (апериодическое) звено:

частотная передаточная функция:

; (3.37)

вещественная составляющая частотной передаточной функции: ; (3.38)

мнимая составляющая частотной передаточной функции:

; (3.39)

модуль частотной передаточной функции (АЧХ): ; (3.40)

аргумент частотной передаточной функции (ФЧХ):

; (3.41)

ЛАЧХ: , (3.42)

причем: L (ω) =20 lg k , при 0 < ωT<< 1,

L (ω) =20 lg k – 20 lg ωT, при Тω >> 1, (3.43)

для построения ЛАЧХ необходимо найти частоту излома (частоту стыковки двух отрезков) согласно формуле:

; (3.44)

частота среза для апериодического звена находится по формуле:

(3.45)

ЛФЧХ: . (3.46)

• Инерционное 2-го порядка (апериодическое) звено:

частотная передаточная функция:

или ; (3.47)

модуль частотной передаточной функции (АЧХ):

или _{; (3.48)}

аргумент частотной передаточной функции (ФЧХ):

, при

, при ; (3.49)

для построения ЛАЧХ необходимо вычислить частоты излома по формуле (3.44) для постоянных времени Т₁ и Т₂ и величину 20 lg k. Результирующая ЛАЧХ звена: , (3.50)

где L₁(w), L₂ (w) – ЛАЧХ двух последовательно соединенных апериодических звеньев 1-го порядка;

ЛФЧХ отличается от ФЧХ только логарифмической шкалой оси частот.

• Инерционное 2-го порядка (колебательное) звено:

частотная передаточная функция:

; (3.51)

вещественная составляющая частотной передаточной функции:

; (3.52)

мнимая составляющая частотной передаточной функции:

; (3.53)

модуль частотной передаточной функции (АЧХ):

; (3.54)

аргумент частотной передаточной функции (ФЧХ):

; (3.55)

ЛАЧХ: ; (3.56)

ЛФЧХ отличается от ФЧХ только логарифмической шкалой оси частот.

• Идеальное интегрирующее звено:

частотная передаточная функция:

; (3.57)

вещественная составляющая частотной передаточной функции:

; (3.58)

мнимая составляющая частотной передаточной функции: ; (3.59)

модуль частотной передаточной функции (АЧХ): ; (3.60)

аргумент частотной передаточной функции (ФЧХ): ; (3.61)

ЛАЧХ: (3.62)

представляет собой прямую линию, которая пересекает ось абсцисс в точке (частота среза) и имеет наклон -20 дБ/дек;

ЛФЧХ не зависит от частоты и проходит параллельно оси абсцисс на расстоянии .

• Идеальное дифференцирующее звено:

частотная передаточная функция:

; (3.63)

вещественная составляющая частотной передаточной функции:

_{; (3.64)}

мнимая составляющая частотной передаточной функции: ; (3.65)

модуль частотной передаточной функции (АЧХ): ; (3.66)

аргумент частотной передаточной функции (ФЧХ): ; (3.67)

ЛАЧХ: , (3.68)

представляет собой прямую линию, которая пересекает ось абсцисс при частоте среза дифференцирующего звена: (3.69)

и имеет наклон +20 дБ/дек;

ЛФЧХ: не зависит от частоты и проходит параллельно оси абсцисс на расстоянии .

• Реальное дифференцирующее звено (дифференцирующее звено с замедлением):

частотная передаточная функция:

_{; (3.70)}

модуль частотной передаточной функции (АЧХ): ; (3.71)

аргумент частотной передаточной функции (ФЧХ): ; (3.72)

ЛАЧХ: , (3.73)

представляет собой ломанную кривую, состоящую из двух отрезков, первый отрезок пересекает ось абсцисс при частоте среза (3.45) и имеет наклон +20 дБ/дек, при частоте излома (3.44) ЛАЧХ становиться параллельной оси абсцисс и располагается на высоте ;

ЛФЧХ отличается от ФЧХ только логарифмической шкалой оси частот.

• Звено запаздывания:

частотная передаточная функция:

; (3.74)

вещественная составляющая частотной передаточной функции:

; (3.75)

мнимая составляющая частотной передаточной функции:

; (3.76)

модуль частотной передаточной функции (АЧХ): ; (3.77)

аргумент частотной передаточной функции (ФЧХ): ; (3.78)

ЛАЧХ: ; (3.79)

ЛФЧХ отличается от ФЧХ только логарифмической шкалой оси частот.

• Консервативное звено:

частотная передаточная функция:

, (3.80)

график этой функции при изменении частоты w от нуля до плюс бесконечности имеет вид двух полупрямых: при изменении частоты w от 0 до резонансной частоты первая полупрямая начинается на вещественной положительной полуоси в точке и идет в бесконечность в положительном направлении; вторая полупрямая начинается в минус бесконечности при и идет по отрицательной вещественной полуоси в начало координат при ;

вещественная составляющая частотной передаточной функции:

; (3.81)

мнимая составляющая частотной передаточной функции: ; (3.82)

АЧХ имеет разрыв на частоте имеет разрыв, соответствующий бесконечному возрастанию амплитуды;

ФЧХ при частоте скачком изменяет фазу от 0 до -p;