4.3. Інтегральна ознака Коші
ТЕОРЕМА. Нехай y=f(x) - неперервна, монотонно спадна і додатна в інтервалі 1,∞) функція, значення якої f(1),f(2), f(3) , …,f(n),… співпадають з відповідними додатними членами ряду
u1+u2+u3+…+un+… (8.15)
Тоді
для збіжності ряду необхідно і достатньо,
щоб невласний інтеграл
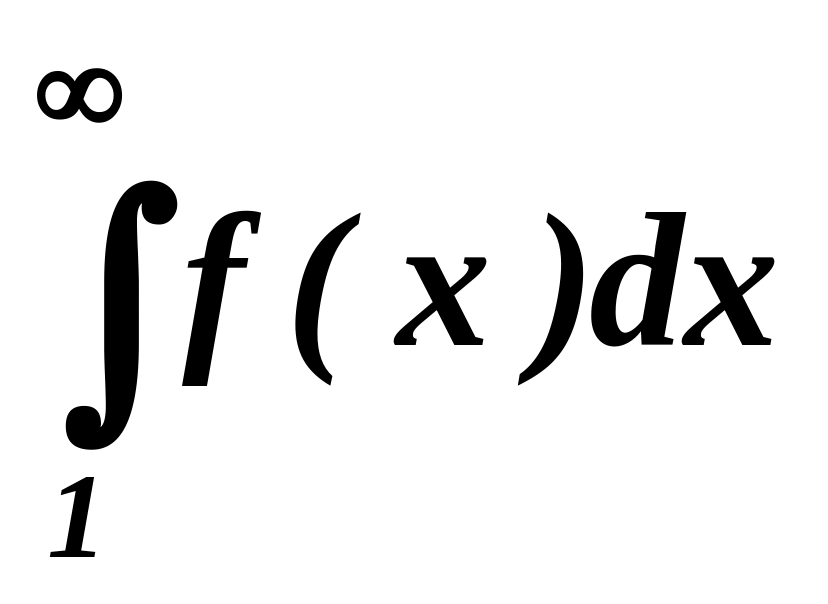мав скінчену величину.
Доведення. Розглянемо криволінійну трапецію , обмежену лінією y=f(x), з основою від x=1 до x=n, де n- довільне ціле додатне число (мал. 1)
Площа фігури, обмежена даними лініями обчислюється за
формулою
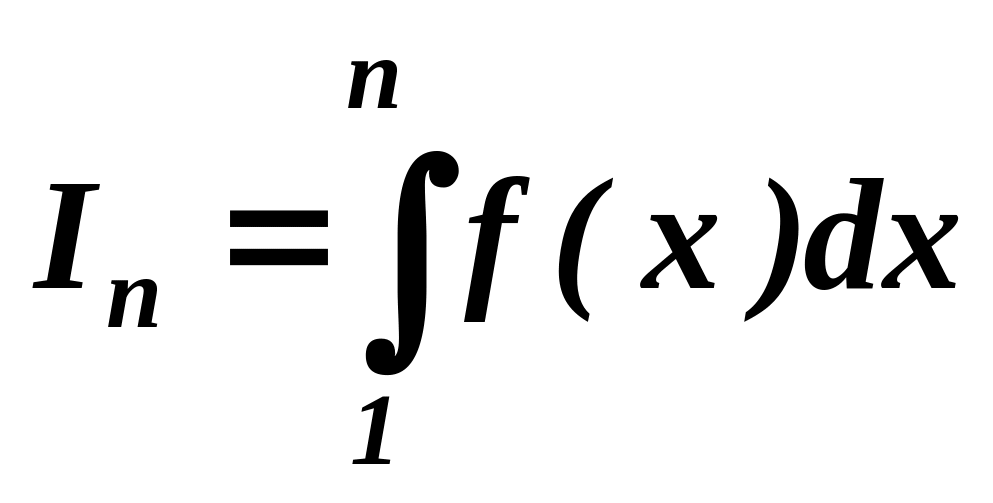(8.16)
Позначимо
цілі точки основи
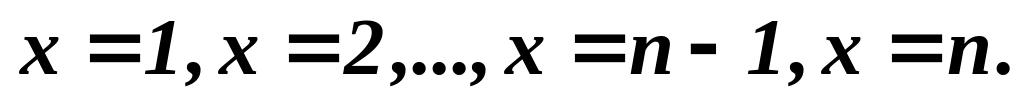
Розглянемо
дві ступінчаті фігури: одна з них
(внутрішня) має площу, яка дорівнює
,
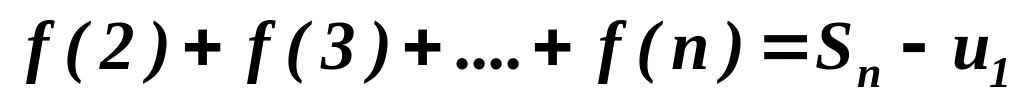а друга