§20.Загальна схема дослідження функції і побудова її графіка

Графік заданої функції можна будувати по довільно взятих

точках. При такому способі можна не виявити всіх особливостей її графіка.

Провівши попередньо дослідження, ми шукаємо характерні для даного графіка точки і тим спрощуємо розв’язок задачі про побудову графіка.

При дослідженні функції і побудові її графіка доцільно

дотримуватися такої схеми:

Перший етап (використання виду заданої функції).

1). Знаходимо область визначення функції, точки розриву;

2). Досліджуємо функцію на парність чи непарність, періодичність;

3). Знаходимо асимптоти графіка функції;

4). Знаходимо точки перетину графіка функції з осями координат.

Другий етап (використання похідної першого порядку).

5). Знаходимо критичні точки першого роду, інтервали

зростання і спадання, точки екстремумів та екстремальні значення функції.

Третій етап (використання похідної другого порядку).

6). Знаходимо критичні точки другого роду, інтервали опуклості і вгнутості, точки перегину та значення функції в цих точках.

Четвертий етап. Складемо таблицю результатів дослідження.

Наносимо отримані точки, асимптоти на координатну площину і будуємо графік функції з урахуванням точок розриву, інтервалів зростання та спадання функцій, проміжків опуклості та вгнутості графіка функцій.

Приклад 1. Дослідити функцію y=x³−3x² та побудувати її графік.

Розв’язування.

1) Область визначення функції : вся числова вісь (−∞,∞)

2). Функція ні парна ні непарна, оскільки

, а тому

Функція не періодична.

3). Вертикальних асимптот графік немає, бо нема точок розриву.

Дослідимо чи графік має похилі асимптоти

Похилих асимптот графік також немає.

4). Знайдемо точки перетину графіка функції з осями координат: при тобто точка

при і

тобто точка

Другий етап.

5). Знаходимо похідну першого порядку:

Знаходимо критичні точки першого роду:

Критичні точки розбивають область визначення на проміжки

( −∞,0)(0,2)(2,∞) (мал.19). Знаходимо знаки похідної в цих проміжках:

Отже, функція зростає на проміжках , спадає на

проміжку .

В точці функція має максимум,

В точці x=2 функція має мінімум,

Третій етап.

6). Знаходимо похідну другого порядку:

Знаходимо критичні точки другого роду: Критична точка розбиває область визначення на проміжки: (мал.20).

Знаходимо знаки другої похідної в цих проміжках:

Отже, графік функції опуклий на проміжку , вгнутий на проміжку . Точка є точкою перегину,

7). Складемо таблицю, де занесемо всі результати дослідження

х	(-∞;0)	0	(0;1)	1	(1;2)	2	(2:∞)
у′	+	0	-	-	-	0	+
у′′	-	-6	-	0	+	6	+
у	 	0 макси-мум	 	-2 перегин	 	-4 мінімум	 

З найдемо ще додатково

Наносимо всі характерні точки на координатну площину і будуємо графік (мал.21).

Приклад 2. Дослідити функцію та побудувати її графік.

Розв’язування. Перший етап.

1). Область визначення функції Функція має розрив в точці

2). Функція ні парна ні непарна, оскільки

і

Функція неперіодична.

3) Оскільки в точці розриву ,

, а

то пряма - вертикальна асимптота.

Дослідимо чи графік має похилі асимптоти

.

.

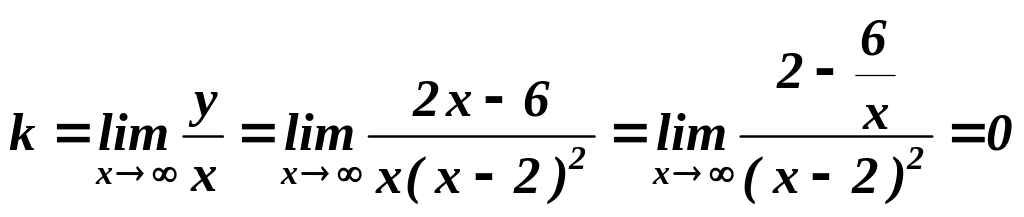Отже, - горизонтальна асимптота.

4). Знайдемо точки перетину графіка функції з осями координат: при тобто точка ; при тобто точка

Переходимо до другого етапу:

5). Знайдемо похідну першого порядку:

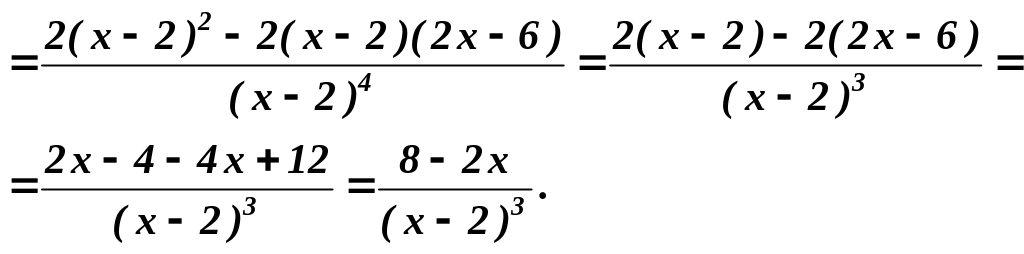
Знаходимо критичні точки першого роду:

Враховуючи точку x=2, де похідна не існує, розіб’ємо область визначення на проміжки (мал.22) і встановимо знаки першої похідної в цих проміжках:

Отже, функція зростає на проміжку , спадає на проміжках В точці функція має максимум,

. Маємо точку

Переходимо до третього етапу:

6). Знаходимо другу похідну:

Знайдемо критичні точки другого роду:

Враховуючи точку , де не існує, розбиваємо область визначення на проміжки: (мал.23).

Встановимо знаки другої похідної в цих проміжках:

Отже, графік функції опуклий на проміжках: , вгнутий на проміжку Точка є точкою перегину,

Маємо точку

7). Складемо таблицю, де занесемо результати дослідження

	(-∞;0)	0	(0;2)	2	(2;3)	3	(3;4)	4	(4;5)	5	(5:∞)
у′	-	-	-	не існує	+	+	+	0	-	-	-
у′′	-	-	-	не існує	-	-	-	-	-	0	+
у	 		 	не існує	 	0	 	0,5	 		 
висновок	Функція Спадає, Графік Опуклий	точка перетину з віссю Оу	Функція спадає, графік опуклий	вертикальна асимптота	Фунція Зростає, Графік Опуклий	точка перетину з віссю Ох	Функція зростає, графік опуклий	Точка перегину	Функція спадає графік опуклий	максимум	Функція спадає, графік опуклий

Б удуємо графік (мал.24).