Работа 7

ОПЕРАТОР ЦИКЛА С ПРЕДУСЛОВИЕМ

Цель работы:

• изучить правила работы с оператором цикла while … do;

• закрепить навыки работы в среде Turbo Pascal.

I. Теоретический раздел работы

1.Введение.

Как указывалось в предыдущей работе, одной из трех основных структур в программировании является цикл. Он используется тогда, когда некоторую часть программы необходимо выполнять многократно для различных значений входящих в нее параметров. Алгоритмы циклической структуры должны содержать следующие элементы:

• подготовка цикла, т.е. задание начальных значений переменных перед первым его выполнением;

• тело цикла, т.е. действия, повторяемые в цикле многократно;

• изменение значений переменных цикла перед каждым новым его выполнением;

• управление циклом, т.е. проверка условия продолжения или окончания цикла и переход к его началу.

В Turbo Pascal имеется несколько возможностей организации цикла в зависимости от того, например, известно или неизвестно число повторений. Отметим, что программно цикл может быть реализован с помощью операторов go to, if и присваивания. Однако, хороший стиль программирования – это программирование без употребления оператора go to. Использование специальных конструкций циклов, рассматриваемых в этой работе, позволяют обходиться без этого оператора, и является более эффективным методом программирования. При их использовании Ваша программа принимает более компактную форму, проще контролируема и более наглядна.

2. Оператор цикла while… do.

Его структура имеет вид:

while B do S;

где B – логическое (булево) выражение;

S - любой оператор языка (тело цикла);

while (пока ), do ( выполнять ) – служебные слова.

Схематически оператор цикла с предусловием можно изобразить таким образом:

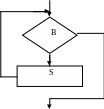
false

true

Такая конструкция цикла организует выполнение оператора S до тех пор, пока логическое выражение B – истинно. Если условие, которое вычисляется и анализируется перед каждым выполнением цикла, - ложно, то выполняется оператор, следующий за while. Заметим, что если первоначальное значение логического выражения B ложно, то оператор S не будет выполняться ни разу. Другая крайность, которую следует избегать,- логическое условие всегда истинно. В этом случае оператор S будет повторяться бесконечное число раз. Произойдет, так называемое, «зацикливание» и тогда потребуются принудительные меры выхода из него,- перезагрузка компьютера.

II. Экспериментальный раздел работы.

Пример 1. Пусть задано натуральное число m. Необходимо найти минимальное число n такое, что факториал n! > m.

По определению, n!=1*2*3*…n.Таким образом, решение поставленной задачи сводится к последовательному увеличению значения n, вычисления n! и сравнения его с заданным числом m. Как только величина n! станет больше m, вычисления нужно прекратить и вывести результат. Последовательное увеличение n организуем с помощью цикла while…do, а для вычисления факториала числа воспользуемся следующими соотношениями:

В этой последовательности первый член равен 1, а каждый последующий равен предыдущему, умноженному на k. Такое соотношение называется рекуррентным, что означает «возвращающийся».

Из школьного курса математики нам известны такого рода соотношения для членов арифметической и геометрической прогрессий, где d – разность, q – знаменатель. Рекуррентные соотношения играют важную роль в программировании, т.к. в сочетании с операторами циклов создают мощный вычислительный инструментарий.

Запишем алгоритм нашей задачи:

1. «подготовка» цикла: ввод m; k=1; p=1;

2. «управление» циклом: если p<m, то выполнять пункт 3 (тело цикла),

иначе выполнять пункт 4 (вывод результата);

3. «тело» цикла: к=к+1; p=p*k; возврат к пункту 2;

4. вывод результата n=k.

Оформим его в виде подпрограммы-функции:

program Example_71;

function Min_N(m:integer):integer;

var k,p:integer;

begin

k:= 1; p:=1;

while (p<m) do

begin Inc(k); p:=p*k end;

Min_N:=k

end;

var m : integer;

Begin

Writeln(‘Введите число m=?’); readln(m);

Writeln(‘ Минимальное значение n=’, Min_N(m)); readln;

End.

Провести отладку и тестирование программы. Вычислить значение n для случаев, когда m=MaxInt и MaxLongInt.

Пример 2. Составим программу вычисления степенной функции , где n – целое натуральное число, x – вещественное.

По определению, , т.е. искомая функция может быть вычислена с помощью цикла путем многократного умножения на х:

Запишем алгоритм вычислений:

1. «подготовка» цикла: ввод n,x; k=1; y=1;

2. «управление» циклом: если k≤n, то выполнять пункт 3 (тело цикла),

иначе выполнять пункт 4 (вывод результата);

3. «тело» цикла: к=к+1; y=y*x; возврат к пункту 2;

4. вывод результата y.

Оформим его в виде подпрограммы-функции:

function Pow_1(n:integer; x:real):real;

var k:integer; y:real;

begin

k:= 1; y:=1;

while (k<=n) do

begin Inc(k); y:=y*x end;

Pow_1:=y

end;

Проведите отладку и тестирование программы. Попытаемся улучшить составленный алгоритм. В нем нужно было выполнить n операций умножения. Заметим, что, например,

, где ,

т.е. для четного n=2*k можно, за счет последовательного применения операций возведения в квадрат, уменьшить число умножений до величины k. Если n=2*k+1, то . Запишем новый вариант программы:

function Pow_2 (n:integer; x:real): real;

var y:real; b:boolean;

begin

b:= true; y:=1;

while b do

begin

if Odd(n) then y:=y*x;

n:=n div 2;

if n>0

then x:=x*x

else b:=false

end;

Pow_2:=y

end;

Здесь введена логическая переменная b, условие n mod 2 =1 заменено логической функцией Odd(n).

Необходимо выполнить тестирование программы и сделать сравнение количества операций двух вариантов программ.

Запишем искомую функцию в виде:

, при n>1 и

, при n=1,

где u=1, если n – четно и u=x, если n нечетно.

Это позволяет составить еще один вариант программы:

function Pow_3 (n:integer; x:real): real;

var u:real;

begin

if Odd(n)

then u:=x

else u:=1;

if n=1

then Pow_3:=x

else Pow_3:=u*sqr(Pow_3(n div 2,x))

end;

Здесь функция Pow_3 вызывает саму себя. Такой прием в программировании называется рекурсивным, но о нем речь пойдем позже. Поэкспериментируйте с разными вариантами программ.

Из процесса работы над этим примером можно сделать очень важный вывод: написав программу – поэкспериментируй с ней; поэкспериментировав, - снова вернись к разработке алгоритма и подумай, как его можно улучшить. Параметры улучшения могут быть связаны с уменьшением количества операций, что приведет к сокращению времени работы программы, с уменьшением объема занимаемой в компьютере памяти, понятностью программы.

Пример 3.Напишем логическую функцию, которая будет возвращать значение true, если натуральное число n простое, и false – в противном случае.

Напомним, что натуральное число называется простым, если оно делится без остатка только на единицу и само себя. Очевидно также, что число n – составное, если оно делится хотя бы на одно из чисел 2,3,…,n-1.

Таким образом, при n>2 необходимо проверить делимость n на каждое из чисел k=2,3, … n-1. На самом деле, как показано в теории чисел, можно сократить сверху диапазон поиска до целой части корня квадратного из n: .

Составим программу на языке Turbo Pascal:

function Simple (n:integer): boolean;

var b:boolean; k,max: integer;

begin

b:= true; max:=trunc(sqrt(n)) + 1; k:=2;

while b and (k<max) do

begin

if n mod k = 0 then b:=false;

Inc(k)

end;

Simple:= b

end;

Поэкспериментируйте с программой. Простые числа 2,3,5,7,11,13,…расположены в натуральном ряду весьма загадочным образом. Двигаясь по этой последовательности чисел необходимо вычислить простое число по его номеру.

Пример 4. Используя алгоритм Евклида, составим программу определения наибольшего общего делителя числа a на b: НОД(a,b).

Один из вариантов этого алгоритма состоит в том, что необходимо последовательно находить остатки от деления :

a на b : ; r₁ = a mod b;

b на ; r₂= b mod r₁;

на ; r₃ = r₁ mod r₂;

..........................

до тех пор, пока не станет равным нулю. Итак,

НОД(a,b) = НОД(b,r₁) = НОД(r₁,r₂) =... = НОД(r_n,0) = r_n .

Например,

НОД(18,12) = НОД(12,6) = НОД(6,0) = 6 .

Напишем подпрограмму-функцию:

function GCD(a,b:integer):integer;

{ Greatest Common Divisor –наибольший общий делитель}

var r1,r2,r3:integer;

begin

if a>b

then begin r1:=a, r2:=b end

else begin r1:=b, r2:=a end;

while r2 <> 0 do

begin

r3:=r1 mod r2;

r1:=r2; r2:=r3

end;

GCD:=r1

end;

Введите, отладьте и протестируйте программу.

Пример 5. Напишем программу, в которой для заданного натурального числа n, ищется число q, записанное цифрами в обратном порядке. К примеру, если n=1965, то q=5691.

Запишем натуральное число n в виде n=a_ka_k-1...a₀ , где a_i - цифры, составляющие его в десятичной системе счисления:

a_ka_k-1...a₀ = a₀10⁰ + a₁10¹ + ... + a_k10^k

Тогда натуральное число q, записанное цифрами в обратном порядке

a₀a₁...a_k = a_k10⁰ + a_k-110¹ + ... + a₀10^k .

Значение a₀ можно найти как остаток от деления числа n на 10. Разделив n на 10, и найдя снова остаток, получим цифру а₁, ... В противоположность этому, число q формируется путем умножения на 10 , полученных остатков от деления числа n. Это последовательное умножение на 10 можно осуществить в виде:

a₀a₁...a_k = a_k + 10( a_k-1 + 10(a_k-2 + ... + 10(a₁ + 10a₀ )...)

Пусть тогда

Теперь нетрудно составить систему рекуррентных соотношений:

которую нужно «прокрутить» в цикле до тех пор пока . Начальное значение искомой величины .

Запишем алгоритм вычислений:

1. «подготовка» цикла: ввод n; k=0; p=n; q=0;

2. «управление» циклом: если p>0, то выполнять пункт 3 (тело цикла),

иначе выполнять пункт 4 (вывод результата);

3. «тело» цикла: a=p mod 10; к=к+1; p=p div 10; q=q*10 +a; возврат к пункту 2;

4. вывод результата q.

Оформим его в виде подпрограммы-функции:

function Inv_N(n:integer): integer;

var a,p,q,k:integer;

begin

k:= 0; p:=n; q:=0;

while (p>0) do

begin

a:=p mod 10; Inc(k);

p:=p div 10; q:=q*10 +a

end;

Inw_N:=q

end;

Отладить, протестировать и провести эксперимент с программой.

Напишите программу перевода чисел из двоичной системы счисления в десятичную; из системы счисления m в систему счисления n.

Ш. Раздел заданий для самостоятельной работы

A.

1. Составить программы.

   1. Дано натуральное число n. Вычислить количество цифр данного числа. Найти ( ).

   2. Определить сумму и произведение цифр целого числа. Найти сумму цифр, больших 5.

   3. Найти максимальную и минимальную цифры числа. Верно ли, что данное число заканчивается на них?

   4. Вычислить сколько раз данная цифра встречается в целом числе. Верно ли, что цифра А, введенная с клавиатуры, не встречается в этом числе?

   5. Определить, является ли данное натуральное число палиндромом, то есть таким, десятичная запись которого читается одинаково слева направо и справа налево. Например, палиндромы 234432, 089980, 5225 .

   6. Составить программу вычисления факториала числа n!=123...n.

   7. Составить программу, которая выдавала бы сообщение ‘ true ‘, если последовательность из N целых чисел, вводимых с клавиатуры, является возрастающей.

   8. Дано целое число. Приписать к нему такое же число.

   9. Найти все трехзначные числа, которые при увеличении на 1 делятся на 2, при увеличении на 2, делятся на 3, при увеличении на 3, делятся на 4, а при увеличении на 4 делятся на 5.

   10. Найти все трехзначные числа, которые при делении на 2, дают остаток 1, при делении на 3, - остаток 2, при делении на 4 – остаток 3, а само число делится на 5.

   11. Найти все делители числа 1234.

2. Составить программы.

   1. Найти наименьшее общее кратное (НОК) чисел а и в, если

НОК(a,b)= ab/ НОД(a,b).

2. Найти наибольший общий делитель трех чисел НОД(a,b,c)=НОД (НОД(a,b),c).

3. Определить, являются ли два натуральных числа a и b взаимно простыми, то есть не имеющих общих делителей, кроме единицы.

4. Некоторая сумма денег S помещается в банк под годовой процент Р. Вычислить, через сколько лет она удвоится.

5. Население города составило на начало года 82 тыс. человек, а годовой прирост, который можно считать постоянным, составил 3.7%.Оперделить, через сколько лет население города составит 150 тыс. человек.

6. В нынешнем году урожай зерновых составил 20 центнеров с гектара. В среднем каждые 2 года за счет применения передовых агротехнических приемов урожай увеличивается на 5%. Вычислить, через сколько лет урожайность достигнет 30 центнера с гектара.

7. Найти двузначное число, обладающее тем свойством, что куб суммы его цифр равен квадрату самого числа.

8. Найти все двузначные числа, сумма квадратов цифр которых делится на 17

9. Найти все трехзначные числа, средняя цифра которых равна сумме первой и второй цифр.

10. Найти все трехзначные числа, средняя цифра которых равна данному целому числу.

11. Проверить, содержит ли квадрат данного натурального числа n, цифру 3 в свой записи.

B.

1. Составить программы.

   1. Дано натуральное число n. Вычислить количество цифр данного числа с использованием цикла и при помощи формулы. Какой способ лучше?

   2. Найти первую и последнюю цифры числа, поменять их местами.

   3. Вычислить сумму четных цифр целого числа, и удалить их.

   4. Если в заданном натуральном числе содержится две одинаковые цифры, программа должна выдавать сообщение.

   5. Вычислить количество симметричных натуральных чисел в промежутке от n до m.

   6. Найти все трехзначные числа, такие, что сумма цифр равна N.

   7. Найти количество различных цифр данного натурального числа.

   8. Найти все четырехзначные числа, в которых есть три одинаковые цифры.

   9. Найти все симметричные четырехзначные числа.

   10. Найти все трехзначные числа, которые состоят из разных цифр, а их сумма равна M.

   11. Найти все натуральные числа из промежутка от 1 до 200, у которых количество делителей равно N.

2. Составить программы.

   1. Найти количество делителей натурального числа, больших K.

   2. Найти сумму четных делителей натурального числа.

   3. Разложить натуральное число на простые множители.

   4. Составить программу, проверяющую, является ли заданное натуральное число совершенным, то есть равным сумме своих положительных делителей, кроме самого этого числа.

   5. Определить, является ли данное натуральное число автоморфным. Автоморфное число равно последним разрядам квадрата этого числа.

   6. Население двух стран равно N₁ и N₂ , а прирост населения P₁ и P₂ , соответственно. Известно, что N₁ > N₂ и P₁ < P₂ . Вычислить, через сколько лет население N₂ превзойдет население N₁.

   7. Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый следующий день он увеличивал дневную норму на 10% от нормы предыдущего дня. Через сколько дней спортсмен будет пробегать в день больше 20 км и, когда суммарный путь будет больше 200 км.

   8. Вычислить, в каких двузначных числах удвоенная сумма цифр равна их произведению.

   9. Найти все трехзначные числа, представляемые в виде суммы факториалов своих цифр.

   10. Можно ли заданное натуральное число m представить в виде суммы квадратов двух натуральных чисел.

   11. Натуральное число из n цифр называется числом Армстронга, если сумма его цифр, возведенная в n-степень, равна самому числу. Составить программу поиска чисел Армстронга в диапазоне от 0 до 2000.

Работа 8

ОПЕРАТОР ЦИКЛА С ПОСТУСЛОВИЕМ

Цель работы:

• изучить правила работы с оператором цикла repeat … until;

• приобрести навыки составления, отладки и тестирования программ, использующих циклы с постусловием;

• закрепить навыки работы в среде Turbo Pascal.

I. Теоретический раздел работы

1. Введение.

Во многих областях математики, физики, техники, экономики приходится сталкиваться с задачей вычисления сумм. В данной работе, вооружившись технологией составления циклических структур repeat…until, рассмотрим некоторые примеры по составлению алгоритмов суммирования рядов на компьютере