
- •Оглавление
- •Введение………………………………………………………..……
- •I. Теоретический раздел работы………………………………………….….
- •I. Теоретический раздел работы…………………………………………….
- •I. Теоретический раздел работы……………………………………………..
- •Работа 1
- •1.Введение.
- •2. Начало работы в среде Turbo Pascal.
- •2.1. Вызов Turbo Pascal.
- •2.2. Использование меню.
- •2.3. Работа с окнами. Использование мыши.
- •2.4. Первая программа.
- •2.5. Работа с файлами
- •2.6. Основные приемы работы с текстовым редактором.
- •2.7. Меню Edit
- •3. В конце работы Вы должны уметь
- •Работа 2 ввод и вывод информации
- •I. Теоретический раздел работы
- •1. Введение.
- •2. Структура программы на языке Паскаль
- •3. Типы данных в языке Turbo Pascal.
- •4. Ввод и вывод данных.
- •II. Экспериментальный раздел работы
- •III. Дополнительный материал.
- •IV. Раздел заданий для самостоятельной работы.
- •Работа 3 расчет по формулам
- •I.Теоретический раздел работы
- •1. Некоторые понятия лексика языка Turbo Pascal.
- •2. Представление вещественных чисел на эвм.
- •3. Оператор присваивания
- •4. Алгебраические выражения.
- •5. Описание пользовательских подпрограмм-функций.
- •II.Экспериментальный раздел работы
- •III. Раздел заданий для самостоятельной работы.
- •Работа 4
- •I.Теоретический раздел работы
- •1. Некоторые сведения о целых типах данных.
- •2. Операции над целыми типами данных.
- •3. Представление целых чисел в компьютере.
- •4. Некоторые стандартные подпрограммы для работы с целыми числами.
- •II.Экспериментальный раздел работы
- •III. Раздел заданий для самостоятельной работы
- •Работа 5 Логический тип данных
- •I.Теоретический раздел работы
- •1. Некоторые сведения о логическом типе данных.
- •2. Логические выражения.
- •3. Основные законы алгебры логики.
- •4. Побитовые операции над целыми числами.
- •Работа 6
- •I.Теоретический раздел работы
- •1. Введение.
- •2. Оператор условного перехода if ... Then...Else
- •3. Условный оператор case...Of
- •II. Экспериментальный раздел работы
- •Работа 7
- •I. Теоретический раздел работы
- •1.Введение.
- •2. Оператор цикла while… do.
- •II. Экспериментальный раздел работы.
- •2. Оператор цикла repeat … until.
- •3. Суммирование рядов.
- •II. Экспериментальный раздел работы Пример 1. Пусть требуется найти сумму ряда:
- •III. Раздел заданий для самостоятельной работы
- •Работа 9 оператор цикла с параметром
- •I. Теоретический раздел работы
- •1. Введение
- •2. Оператор цикла for …do
- •3. Операторы завершения цикла
- •4. Алгоритм Горнера.
- •II. Экспериментальный раздел работы
- •III. Раздел заданий для самостоятельной работы
- •Список литературы
4. Побитовые операции над целыми числами.
Логические операции применимы и к операндам целого типа. Если операнды – целые числа, то результат логической операции тоже целое число. Они действуют побитно согласно описанию, данному в следующей таблице:
Операнды Результат операции
A B not A A and B A or B A xor B
0 0 1 0 0 0
0 1 1 0 1 1
1 0 0 0 1 1
1 1 0 1 1 0
Например,
Not 00000111 => 11111000
00011100 and 01110011 => 00010000
00011100 or 01110011 => 01111111
00011100 xor 01110011 => 01101111
П. Экспериментальный раздел работы
Пример 1. Проверка таблиц истинности.
program Example_51;
var p,q :boolean;
begin
a:=true; b:=true; {Ввод данных}
writeln (‘p=’, p,’ q=’,q,’ p and q =’, p and q); {Вывод результата}
readln
end.
Измените программу, проведите проверку таблиц истинности основных булевых операций и законов математической логики.
Пример 2. Напишем программу, в которой логическая переменная принимает значение true, если, случайным образом выбранная, точка с координатами (x,y) попадает внутрь кольца с центром в начале координат и радиусами 0.1 и 0.6, иначе - логическая переменная принимает значение false.
program Example_52;
var x,y: real;
p:boolean;
begin
{Ввод данных}
Randomize;
x:=Random; y:=Random; writeln(‘x=’,x:8:5,’ y=’,y:8:5);
{Расчет}
p:= (sqr(x) + sqr(y) > 0. 01) and (sqr(x) + sqr(y)) < 0.36);
{Вывод результата}
writeln (‘p=’, p); readln
end.
Поэкспериментируйте с программой. Замените логическое выражение на
p:= not( (sqr(x) + sqr(y) < 0. 01) or (sqr(x) + sqr(y)) > 0.36));
Основываясь на законах де Моргана, объясните полученные экспериментальные результаты.
Пример 3. Составим программу, результатом работы которой будет удаление из двоичного представления данного натурального числа i-го бита.
program Example_53;
var n,x,y,z,k: integer;
begin
{Ввод данных}
writeln(‘Введите значение натурального числа n=?’ ); readln(n);
writeln(‘Введите номер вычеркиваемого бита k=?’ ); readln(k);
{Расчет}
x:=1 shl k;
y:= not x;
z:=n and y; {Можно было написать z:=n and not(1 shl k)}
{Вывод результата}
writeln(‘x=’,x,’ y=’,y,’ z=’,z);readln
end.
Необходимо разобраться с алгоритмом программы, провести тестовый расчет.
Составьте программу, выполняющую побитовые операции not, and, or, xor с целыми числами. Поясните смысл полученных результатов.
Пример 4. Дайте объяснение результатам следующей программы.
program Example_54;
begin
writeln(1365 and 2730);
writeln(1365 or 2730);
writeln(1365 xor 2730);
writeln(1365 and $FF);
writeln(1365 and $FF0);
writeln(1365 and $FF00);
end.
Для объяснения полученных результатов переведите числа в двоичную систему счисления. Поэкспериментируйте с программой. Убедитесь, например, что -256 and 255 =0; -256 or 255 = -1; -256 xor 255 = -1. Вспомните, что для представления отрицательных чисел в компьютере используется дополнительный код.
Знак $ означает, что число записано в шестнадцатеричной системе счисления, в которой для обозначения цифр 10,11,12,13,14,15 используются буквы A, B, C, D, E, F.
Ш. Раздел заданий для самостоятельной работы
A.
Вычислить значение логического выражения при всех возможных значениях логических величин А и В:
А или В; А и В; В или С.; А или В и не С; А и не В или С; не А или не В;
А или не В;А и В или С; А и (А или не В); (не А или В) и В; не А и не В или А;
А и (не В или С);В или не(А и не В); В или не А и не В; не (не А и не В) или А;
не А и не В; не (не А или не В) или А; не (А и С) или В; А и (не (В или С));
не (не А или не В) и В; А или не (А и В) или С; не А или А и (В или С);
(А или В и не С) и С; (не А или не В) и не С; (не А или не В) и (А или В);
А и В или А и С или не С; не (А или не В и С); А и не (В или не С);.
не (А или не В и С) или С; не (не А или В и С); не (А и не В или С) и В;
не (не А или В и С) или А; не (А и В) и (не А или не С); не (А и не В) или (А или не С);
Вычислить значения логических выражении:
 при х= 1, у=-1;
при х= 1, у=-1;(
 0)
или (
0)
или ( 4)
при
4)
при

( 0) и ( 4) при
 и
и
 при
при
 ;
;или
 при
;
при
;(не (
 и (у > х) при
;
и (у > х) при
;(не ( или (у > х) при
 .
. при
при

 или (
4)
при
или (
4)
при
 ;
;(
 )
и (
)
и ( >
4) при
>
4) при

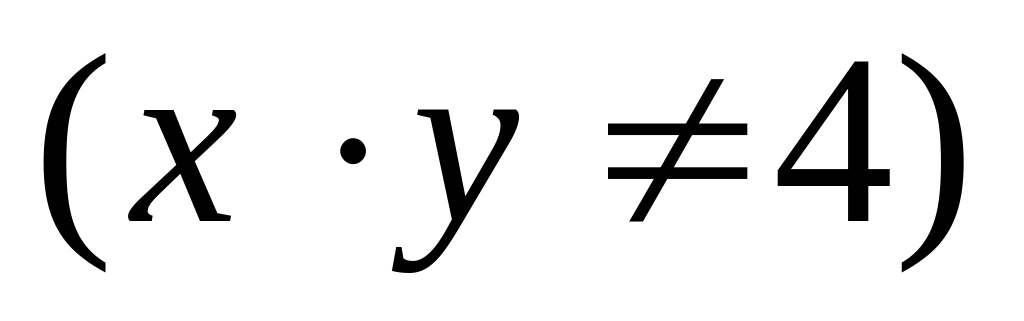 и
при
и
при
или при ;
(не (
 и (у > х) при
и (у > х) при
(не ( и (у > х) при ;
Записать условие, которое является истинным, когда
каждое из чисел А и В больше 100;
только одно из чисел А и В четное;
хотя бы одно из чисел А и В положительно;
каждое из чисел А, В, С кратно трем;
только одно из чисел А, В и С меньше 50;
хотя бы одно на чисел А, В, С отрицательно.
каждое из чисел X и У нечетное;
только одно из чисел X и У меньше 20;
хотя бы одно из чисел X и У равно нулю;
каждое из чисел X, У, Z отрицательное;
только одно из чисел X, Y и Z кратно пяти;
хотя бы одно из чисел X, Y, Z больше 100.
целое А кратно двум или трем;
целое А не кратно трем и оканчивается нулем.
целое N кратно пяти или семи;
B.
Вычислить значение логического выражения при всех возможных значениях логических величин X, Y и Z:
не (X или Y); не X и Y; X и не Y; X или Z; (не X или Y) и Y; X или (не X и Y);
X или не Y; X или Y и Z; не(X и не Y) или X; Y и не X или не
 ;
не Y и не X
или Y;
;
не Y и не X
или Y;не X и не Y; не (не X и Y) или не X; не (не X и не Y) и X; не (X или не Y) или не Y;
не (X и Z) или Y; е) X и (не (Y или Z)). не X и не Y; X и (не Y или Z);
X или Y и не Z; X и не Y или Z; X и не (Z или Y) или не Z; не X или X и (Y или Z);
(X или Y и не Z) ; не X или не Y или не Z; (не X или не Y) и (X или Y);
X и Y или X и Z или не Z; не (X или не Y и Z); Y или (X и не Y или Z);
не (не X и Y или Z); не (У или не X и Z) или Z; X и не (не Y или Z) или Y;
не (X или Y и Z) или не X; не (X или Y) и (не X или не Z);
не (не X и Y) или (X и не Z); в) X или не Y и не (X или не Z).
Составьте программу проверки эквивалентности двух логических функций. Постройте соответствующие таблицы истинности(программно).
Проверьте что X → Y эквивалентна not (x) or y
Проверьте что X │ Y (Функция Шеффера) эквивалентна not (x) or not(y)
Проверьте что X ↓ Y (Функция Вебба, или стрелка Пирса) эквивалентна not (x) and not (y)
Дана некоторая логическая функция, например, ( x→y)→z. Постройте таблицу истинности данной функции. Преобразуйте эту формулу в эквивалентную ей. Составьте программу проверки эквивалентности этих двух логических формул.
Дана логическая функция ( x │ y) │ z. Постройте таблицу истинности данной функции. Преобразуйте эту формулу в эквивалентную ей. Составьте программу проверки эквивалентности этих двух логических формул.
Дана логическая функция ( x ↓ y) ↓ z. Постройте таблицу истинности данной функции. Преобразуйте эту формулу в эквивалентную ей. Составьте программу проверки эквивалентности этих двух логических формул.
Дана логическая функция ( x → y) and z. Постройте таблицу истинности данной функции. Преобразуйте эту формулу в эквивалентную ей. Составьте программу проверки эквивалентности этих двух логических формул.
Дана логическая функция not ( x or not y and z). Постройте таблицу истинности данной функции. Преобразуйте эту формулу в эквивалентную ей. Составьте программу проверки эквивалентности этих двух логических формул.
Дана логическая функция x and not ( y or not z). Постройте таблицу истинности данной функции. Преобразуйте эту формулу в эквивалентную ей. Составьте программу проверки эквивалентности этих двух логических формул.
Дана логическая функция not ( not x or y and z). Постройте таблицу истинности данной функции. Преобразуйте эту формулу в эквивалентную ей. Составьте программу проверки эквивалентности этих двух логических формул.
Дана логическая функция ( x ↓ y ) ↓ ( z ↓ v). Постройте таблицу истинности данной функции. Преобразуйте эту формулу в эквивалентную ей. Составьте программу проверки эквивалентности этих двух логических формул.
Вывести на экран True при выполнении условия
х принадлежит отрезку [2,5] или [-1,1];
x лежит вне отрезков [2,5] и [-1,1];
только одно из чисел x, y и z положительно;
из чисел x, y и z только два равны между собой;
уравнение ax2+bx+c=0 не имеет вещественных корней;
a = max (a, b, c, d) ;
целые n и k имеют одинаковую чётность;
поля (г1, в1) и (г2, в2) шахматной доски имеют одинаковый цвет.
ферзь, расположенный на поле (г1, в1) шахматной доски, "бьет" поле(г2, в2).
число n нечетное.(Напишите свой вариант функции odd, возвращающей значение "Истина", если её целочисленный аргумент имеет нечетное значение).
