
- •Математика
- •8 Класс
- •8 Класс Решения
- •9 Класс. Время выполнения 2 часа. Задача 1.
- •Задача 2.
- •З адача 3.
- •З адача 4.
- •Районная олимпиада по физике 2012/2013 уч. Г.
- •9 Класс
- •9 Класс
- •8 Класс
- •9 Класс
- •Муниципальный этап 2011–2012 уч. Г.
- •8 Класс
- •8 Класс
- •8 Класс
- •Ключи школьной олимпиады.
- •8 Класс
8 Класс
8.1. Вычислить
![]()
8.2. При каких значениях m уравнения mx – 1010 = 1001 и 1001x = m – 1010x имеют общий корень?
8.3. Через вершины А и С треугольника АВС проведены прямые, перпендикулярные биссектрисе угла АВС. Они пересекают прямые СВ и ВА в точках К и М соответственно. Найдите длину АВ, если ВМ = 8 см, KC = 1 см и АВ > ВС.
8.4. В трех ящиках лежат орехи. В первом ящике на 6 кг орехов меньше, чем в двух других вместе. А во втором — на 10 кг меньше, чем в двух других вместе. Сколько орехов в третьем ящике? Решить логически.
Для каждой из изображенных на рисунке фигур придумайте способ разрезать ее на две части, из которых можно сложить квадрат.

Ключи школьной олимпиады.
8 Класс
1. Обозначим за x = 201120112011. Вычислим знаменатель рассматриваемой дроби: x² – (x – 1)(x + 1) = x² – (x² – 1) = 1. Значит, величина дроби равна ее числителю, то есть 2011.
Ответ: 2011.
2. Корнями данных уравнений являются числа 2001/m и m/2001 соответственно. Тогда 2001/m =m/2001 , m2 = 20112 , m = ±2011.
Ответ: при m = ±2011.
3. В треугольниках ABK и MBC биссектрисы одновременно являются и высотами (см. рис.), поэтому эти треугольники — равнобедренные. Так как АВ > ВС, то точка M лежит на стороне АВ, а точка K — продолжении стороны ВС. Значит, BC = BM = 8 (см); AB = BK = BC + CK = 9 (см).
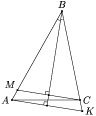
Ответ: AB = 9 см.
4. Соединим оба заданных условия и получим следующее утверждение: "В первом и втором ящиках орехов на 6 кг+10 кг меньше, чем в первом, втором и двух третьих". Отсюда следует, что в двух третьих ящиках 16 кг орехов, т.е. в третьем ящике 8 кг орехов.
Ответ: 8 кг.
5. Обратим внимание, что каждая из указанных фигур состоит из 16=4·4 клеток, значит, квадрат получится размера 4×4. Дальше надо постараться «увидеть» часть этого квадрата на рисунке и часть фигуры, которую надо отрезать и передвинуть.

