ИСХОДНЫЕ ДАННЫЕ

Таблица 1 – Исходные данные к контрольной работе

Параметры группы генераторов Г1	Параметры генератора Г2	Параметры группы трансформаторов Т1	Параметры трансформатора Т2

где: , – номинальная активная мощность генератора Г1;

, – номинальные коэффициенты мощности генераторов Г1, Г2;

, – синхронные сопротивления по продольной оси генераторов Г1, Г2;

, – переходные сопротивления по продольной оси генераторов Г1, Г2;

, – сопротивления обратной последовательности генераторов Г1, Г2;

, – постоянные времени генераторов Г1, Г2;

, – номинальная мощность трансформаторов Т1, Т2;

, – коэффициенты трансформации трансформаторов Т1, Т2;

, – напряжение короткого замыкания трансформаторов Т1, Т2;

– сопротивление нулевой последовательности нагрузки в относительных единицах при базисной мощности

Напряжение на шинах потокораздела системы .

Параметры линии электропередачи (одна цепь) ; ; . Длина ЛЭП = 375 км.

Параметры нагрузки: – активная мощность нагрузки; – коэффициент мощности нагрузки;

– мощность, передаваемая от группы генераторов Г1 в исходном режиме.

– коэффициент мощности группы генераторов Г1 в исходном режиме.

1. РАСЧЕТ СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ СИСТЕМЫ

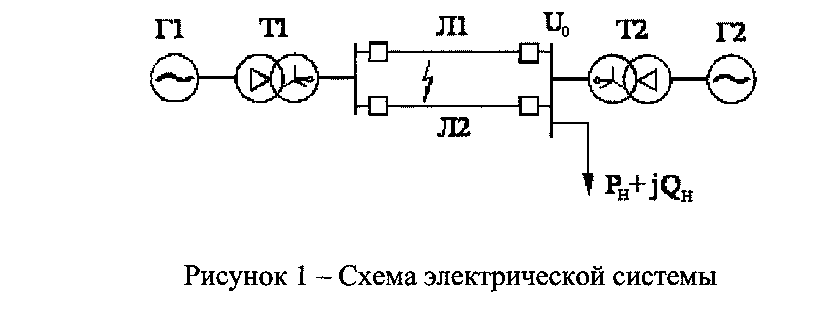
Для электрической системы, схема которой приведена на рисунке 1, определим идеальные пределы мощности генераторов Г1 первой станции ЭС-1 и коэффициенты запаса статической устойчивости при передаче мощности от первой станции к точке потокораздела. Примем напряжение в точке потокораздела неизменным.

1.1 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ СХЕМЫ ЗАМЕЩЕНИЯ СИСТЕМЫ ЭЛЕКТРОСНАБЖЕНИЯ

Расчет будем вести в относительных единицах. Для этого примем следующие базисные величины:

• базисное напряжение ;

• базисная мощность .

Составим схему замещения электрической системы:

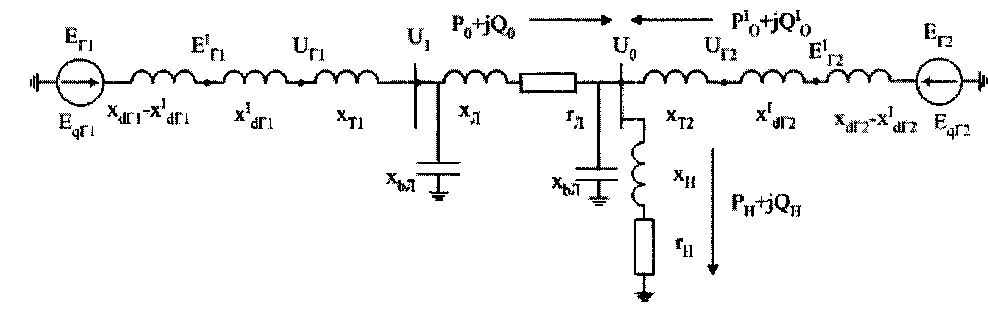
Рисунок 2 - Схема замещения электрической системы

Определим параметры схемы замещения. При этом модули индуктивных сопротивлений будем умножать на , а модули емкостных сопротивлений на .

Синхронные сопротивления генераторов Г1:

Сопротивления генератора Г2:

Сопротивление трансформатора Т1:

Сопротивление трансформатора Т2:

Параметры ЛЭП:

Проводимость и зарядная мощность линии:

Напряжение на нагрузке:

Определим параметры режима работы системы в относительных единицах.

Мощность первого генератора:

(здесь ).

Мощность второго генератора:

(здесь ).

Мощность нагрузки:

(здесь ).

Сопротивление нагрузки:

Мощность, поступающая от генераторов Г1 в рабочем режиме:

(здесь ).

Мощность, поступающая от генератора Г2:

Сопротивления от генераторов до нагрузки:

Так как дальнейший расчет будем производить в относительных единицах, то символ (*) можно опустить.

1.2 Определение характеристик системы при условии пренебрежения активным сопротивлением линии и зарядной мощностью ( )

В этом случае схема замещения (рисунок 2) примет вид, показанный на рисунке 3.

Определим ток, протекающий от генераторов Г1 до точки потокораздела:

Полное сопротивление цепи от генераторов до точки потокораздела составляет:

Сопротивление от точки потокораздела до шин генераторов Г1:

Определим напряжение на шинах генераторов Г1:

ЭДС генераторов Г1:

(здесь – угол нагрузки в рабочем режиме).

Для определения переходной ЭДС генераторов Г1 необходимо представить схему замещения (рисунок 2)в виде, изображенном на рисунке 4.

Рисунок 4 – Схема замещения для определения переходной ЭДС генераторов Г1

Определим переходное сопротивление цепи от точки потокораздела до генераторов Г1:

Определим переходную ЭДС генераторов Г1:

( – угол переходной ЭДС в рабочем режиме)

На основании полученных данных строим векторную диаграмму генераторов Г1 (рисунок 5).

Рисунок 5 – Векторная диаграмма системы при условии r_л = 0 и Q_З = 0

1.2.1 ХАРАКТЕРИСТИКИ СИСТЕМЫ ПРИ ОТКЛЮЧЕННОМ АРВ

Определим угловую характеристику генераторов Г1 для выбранных условий (АРВ отключено):

График угловой характеристики представлен на рисунке 6.

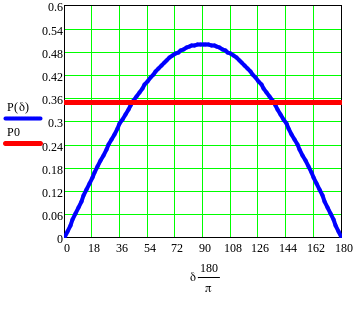
Рисунок 6- Угловая диаграмма генераторов Г1 при условии (АРВ отсутствует) (здесь мощность, отдаваемая генераторами Г1 в рабочем режиме)

Определим идеальный предел мощности

Определим коэффициент запаса устойчивости генераторов Г1:

1.2.2 ХАРАКТЕРИСТИКИ СИСТЕМЫ ПРИ ВКЛЮЧЕННОМ АРВ ПД

При включенном АРВ ПД считаем, что переходная ЭДС генераторов Г1 постоянна (действует схема замещения, изображенная на рисунке 4)

Определим проекцию вектора на ось (см. векторную диаграмму на рисунке 5):

Проекция вектора на ось :

Характеристика мощности генератора:

Угловая характеристика генераторов Г1 представлена на рисунке 7.

Рисунок 7- Угловая диаграмма генераторов Г1 при условии (включено АРВ ПД) в сравнении с угловой диаграммой без АРВ

Определим максимум полученной зависимости. Для этого найдем первую производную по углу и приравняем ее к нулю

Уравнение равно нулю при .

При этом функция , т.е. достигает максимума.

Определим коэффициент запаса статической устойчивости по активной мощности.

1.2.3 Характеристики системы при включенном арв пд

АРВ СД поддерживает постоянным напряжение на шинах генератора . При этом схема замещения (рисунок 2) примет вид, представленный на рисунке 7.

Рисунок 7 – Схема замещения электрической системы при включенном АРВ СД

Угловая характеристика мощности генераторов Г1 в этом случае имеет вид:

График угловой характеристики генератора при включенном АРВ СД в сравнении с угловыми характеристиками генератора с включенным АРВ ПД и без АРВ представлен на рисунке 8.

Рисунок 8 – Характеристика мощности генератора при включенном АРВ СД (верхняя линия) (максимальное значение мощности Рм = 1,616) в сравнении с характеристикой с АРВ ПД (средняя линия) и без АРВ (нижняя линия)

Определим максимум полученной зависимости. Для этого найдем первую производную по углу δ и приравняем ее к нулю. Коэффициент запаса статической устойчивости

1.3 ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК СИСТЕМЫ ПРИ УСЛОВИИ УЧЕТА АКТИВНОГО СОПРОТИВЛЕНИЯ ЛИНИИ И ПРЕНЕБРЕЖЕНИЯ ЗАРЯДНОЙ МОЩНОСТЬЮ

1.3.1 ХАРАКТЕРИСТИКИ СИСТЕМЫ ПРИ ОТКЛЮЧЕННОМ АРВ

Активное сопротивление линии электропередачи равно . При учете активного сопротивления схема замещения примет вид, представленный на рисунке 9.

Рисунок 9 ­ Схема замещения при учете активного сопротивления линии электропередачи

Полное сопротивление цепи от генератора до точки потокораздела равно:

ЭДС генераторов Г1 равно:

здесь – угол нагрузки генератора в рабочем режиме.

Векторная диаграмма системы при учете активного сопротивления ЛЭП представлена на рисунке 10.

Рисунок 10 – Векторная диаграмма системы при учете активного сопротивления ЛЭП

Для определения угловой характеристики системы представим линию электропередачи в качестве четырехполюсника, состоящего из одного сопротивления Коэффициенты такого четырехполюсника (см. приложение 2) таковы:

Собственные проводимости равны:

Взаимные проводимости равны:

Определим углы и :

Угловая характеристика определяется выражением:

График угловой характеристики представлен на рисунке 11.

Рисунок 11 – Угловые характеристики генераторов Г1 (с отключенным АРВ) с учетом активного сопротивления линии (верхняя кривая) и без учета (нижняя кривая)

Из характеристики видно, что наличие активного сопротивления линии электропередачи увеличивает максимальную передающую мощность генератора (в нашем случае максимальная передающая мощность достигает )Кроме того, график мощности немного смещается вправо в сторону больших углов нагрузки.