1 Вопрос

Предмет, первичные понятия теоретической механики.

Все явления природы представляют собой движение, и всякое изменение материи называют движением.

Теоретическая механика является естественной наукой о наиболее общих законах механического движения. Под механическим движением подразумевают изменение положения материальных тел в пространстве относительно друг друга с течением времени. Материальным телом, или макротелом, называют тело, размеры которого можно измерить измерительными инструментами, например, обычной ученической линейкой, электронным микроскопом или радиотелескопом.

Первичными называют понятия, которые, как и аксиомы, принимают без определения. Первичными понятиями теоретической механики являются пространство и время. Пространство в теоретической механике принято трехмерным, подчиняющимся геометрии Евклида. Время принято одинаковым во всех точках пространства, не зависящим от движения. В результате получена картина мира, которая для современного образованного человека стала обыденной.

Система отсчета.

В теоретической механике системой отсчета называют тело, относительно которого исследуется движение (тело отсчета), и связанную с ним систему координат. Часы в систему отсчета не входят, так как время во всех точках пространства одинаково и не зависит от движения (абсолютное время).

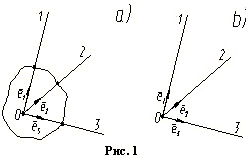   Пространство трехмерное, поэтому систему координат образуют три оси 1,2,3 со своими единичными векторами . Оси связаны с телом и пересекаются в одной точке O (рис. 1, a). Ниже будет показано, что движение системы координат полностью определяет движение тела отсчета, поэтому обычно тело отсчета на рисунках не изображают, считая, что оно находится в начале координат - точке O. В результате изображение системы отсчета совпадает с изображением системы координат (рис. 1, b). А так как часы в систему отсчета не входят, то в теоретической механике систему отсчета часто называют просто системой координат.

На рис. 1, b изображена косоугольная система координат. Она неудобна для применения на практике. Самой удобной в этом смысле является прямоугольная или декартова система координат (рис. 2). Она широко используется в науке и технике, ее оси получили специфические названия. Ось 1 названа осью абсцисс и обозначена X, ось 2 названа осью ординат и обозначена Y, ось 3 названа осью аппликат и обозначена Z. Единичные векторы названы ортами и обозначены как соответственно.

Р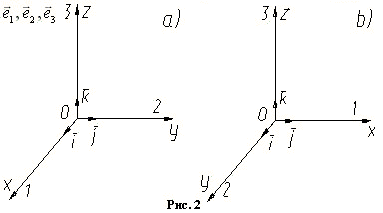 азличают правые и левые декартовы системы координат. В правой системе координат вращение оси X к оси Y по кратчайшему угловому расстоянию наблюдается с конца оси Z против хода часов, а в левой - по ходу часов. На рис. 2, a изображена правая система координат, а на рис. 2, b - левая.

Для механических явлений безразлично, какая система координат используется. Однако для микромира, как показано в теоретической физике, в правых системах координат картина мира описывается более правильно. Это обусловило более широкое применение правых систем координат. Поэтому при изложении материала, если не оговорено специально, будем называть системой отсчета тело отсчета и связанную с ним правую прямоугольную или декартову систему координат, а правую прямоугольную или правую декартову систему координат - просто системой координат.

Следует отметить, что механическое движение исследуется и в других системах координат - сферической, цилиндрической, полярной, которые относятся к криволинейным системам координат. Из них, например, сферическая система координат широко используется в географии, астрономии, навигации и в военном деле.

Методы и модели теоретической механики.

Основным методом теоретической механики, как любой естественной науки, является диалектический метод.

Суть метода заключается в переходе от живого созерцания к абстрактному мышлению, а затем к практике, что происходит в непрерывном развитии. Применительно к механике это означает опыты и наблюдения за механическими явлениями с целью выявления закономерностей в них. Затем закономерности осмысливаются, некоторые из них принимаются за истины, не требующие доказательств - первичные понятия и аксиомы. На основании первичных понятий и аксиом доказываются теоремы и законы теоретической механики, истинность которых проверяется на практике путем проведения опытов и наблюдений.

Иными словами, теоремы и законы теоретической механики построены на многовековом опыте наблюдения за механическими явлениями и постоянно проверяются практической деятельностью человечества, начиная с эксплуатации простейших механизмов - клина и рычага, кончая полетами в пределах Солнечной системы. Здесь же отметим, что в ходе исторического развития механические опыты и наблюдения за механическими явлениями выделились в наблюдательную (экспериментальную) механику. В настоящее время наблюдательная механика прямо не входит в теоретическую механику, однако ее разделы существуют в экспериментальной физике, астрономии и технических науках.

Вторым по значимости методом теоретической механики является метод абстракций. Суть метода станет ясна, если мы раскроем смысл слова абстрагировать. В переводе с греческого языка абстрагировать - выделять основное, существенное и отбрасывать второстепенное, несущественное.

Применение метода для исследования механического движения привело к тому, что в теоретической механике изучается движение не реальных материальных тел, а их абстрактных моделей. Таких моделей три.

Материальная точка - точка, обладающая массой и инерционными свойствами.

Система материальных точек - любая совокупность материальных точек.

Абсолютно твердое тело - тело, в котором расстояние между двумя любыми точками не изменяется.

В ряде разделов механики тело рассматривается как система материальных точек, непрерывно заполняющих объем тела. За абсолютно твердое тело принимается неизменяемая система материальных точек, непрерывно заполняющих объем тела.

Сравнивая модели с реальными материальными телами, видим, что уровень абстракции моделей высок. Трудно себе представить тело, не имеющее размеров, обладающее массой и участвующее в механических взаимодействиях.

Третьими по значимости методами теоретической механики являются математические методы. Особенно широко применяются методы аналитической геометрии, векторной алгебры, дифференциального и интегрального исчисления.

Границы применения законов теоретической механики.

Границы применения законов теоретической механики, как и любой естественной науки, устанавливаются опытом. На современном этапе развития науки и техники экспериментально установлено, что для макротел законы теоретической механики истинны на расстояниях от разрешающей способности электронного микроскопа до предела дальности современного радиотелескопа на скоростях до скорости выхода за пределы Солнечной системы.

Наука и техника все время развиваются. По мере углубления наших знаний изменяются и границы истинности теоретической механики. Выяснилось, что теоретическая механика ограниченно применима для изучения микромира и, что для изучения движения элементарных частиц - электрона, протона и др. нужно применять релятивистскую механику. В релятивистской механике приняты иные первичные понятия. Пространство подчиняется геометрии Римана, время не абсолютно, а зависит, как и пространство, от движения. В результате была получена картина мира иная, чем в классической механике.

Следует отметить, что к настоящему времени экспериментального подтверждения истинности законов релятивистской механики для движения макротел не получено. Сейчас законы и методы теоретической механики с высокой точностью удовлетворяют требованиям современных отраслей техники.

Место теоретической механики среди естественных наук

Сегодня под механикой следует понимать совокупность достаточно обособленных отраслей знаний, базирующихся на первичных понятиях и аксиомах классической или теоретической механики.

В самой же современной теоретической механике изучается сравнительно узкий круг вопросов механики, а именно: механика материальной точки, механика абсолютно твердого тела и механика их систем.

Это произошло потому, что в ходе исторического развития ряд разделов теоретической механики, вследствие специфики объектов исследования и применяемых математических методов, становятся вполне самостоятельными науками. В этих науках обычно к моделям и законам теоретической механики добавляются новые модели и законы, характеризующие дополнительные свойства материальных тел.

В механике сплошной среды добавляется новая абстрактная модель - сплошная среда. В теории упругости и сопротивлении материалов учитываются деформации тел и добавляется закон о связи деформаций с силами. В гидродинамике учитывается скорость деформации и используется дополнительный закон о связи скоростей деформации и сил. В газовой динамике или аэродинамике, кроме того, учитывается сжимаемость газа.

В теоретической механике зародилась теория автоматического управления. Ее связывают с механикой не только исторические корни и общие методы, в ее основе лежат разделы теоретической механики - устойчивость равновесия и движения, теория колебаний. Указанные разделы часто излагаются в современном курсе теоретической механики, хотя они достаточно давно стали самостоятельными науками.

Механика вообще и теоретическая механика, в частности, имеют свою историю становления и непрерывно развиваются. Наибольший вклад в основу современной теоретической механики внесли великие ученые Галилей (1564 - 1642) и Ньютон (1643 - 1727). Вклад Ньютона настолько велик, что классическую механику часто называют ньютоновой механикой. Он обобщил знания в области механических явлений, сформулировал первичные понятия и аксиомы классической механики.

Дальнейшее развитие теоретической механики связано с именами многих ученых, наиболее выдающиеся из которых Даламбер (1717 - 1783), Эйлер (1707 - 1783), Лагранж (1736 - 1813). Русские ученые также внесли свой вклад в развитие теоретической механики. Из них более известны М.В. Остроградский (1801 - 1862), Н.Е. Жуковский (1847 - 1921), А.М. Ляпунов (1851 - 1918).

В последние десятилетия развитие механики связано с ракетостроением, практической космонавтикой или аэронавтикой. Здесь вклад русских и советских ученых велик. Основополагающие работы в этой области принадлежат И.В. Мещерскому (1859 - 1935), К.Э. Циолковскому (1857 - 1935), С.П. Королеву (1906 - 1966).

Разделы теоретической механики.

Теоретическая механика делится на три раздела: статику, кинематику и динамику.

Статика - учение о равновесии под действием сил.

Кинематика - учение о движении без учета сил.

Динамика - учение о движении под действием сил.

Так как равновесие - частный случай движения, то статику и динамику часто объединяют в один раздел, который называют кинетикой.