§ 2. Годографы волн.

Годограф - это график зависимости времени вступления (экстремума) волны от координат точек наблюдений. Уравнение годографа

Кажущаяся скорость (V*) - скорость распространения волны вдоль линии наблюдений

(1.14)

Для плоской волны

(1.15)

где - угол выхода волны на поверхность;

- истинная скорость волны в среде.

Годограф прямой волны в однородной среде при наблюдении на прямолинейном продольном профиле является наклонной прямой линией (рис. 3). Уравнение годографа

(1.16)

Кажущаяся скорость прямой волны равна истинной скорости

Годограф отраженной волны от плоской отражающей границы, нак­лоненной под углом к линии наблюдений, и при однородной покрывающей толще со скоростью представляет собой гиперболу. Уравнение годографа (рис. 3)

(1.17)

в случае горизонтальной границы принимает вид

(1.18)

Кажущаяся скорость отраженной волны

(1.19)

меняется от при до при .

Годограф преломленной (головной) волны.

При условии, что > (рис. 3), лучи сферической волны, падающие на границу под критическим углом ( ), во второй среде скользят вдоль границы. Так как > , то волна, рас­пространяющаяся во второй среде вдоль границы, обгонит прямую вол­ну в первой среде. По принципу Гюйгенса, каждая точка фронта этой волны является источником вторичных сферических волн в первой среде. Фронты и лучи вторичных волн в первой среде определяются нес­ложным геометрическим построением. Вторичная (головная или прелом­ленная) волна распространяется в первой среде коническим фронтом под углом i к границе. Начальный луч головной волны, проходящий через точку М, совпадает с лучом отраженной волны. На участке 0В (рис. 3) головная волна отсутствует - "мертвая зона". Точка F является начальной точкой годографа головной волны, она совпадает с точкой годографа отраженной волны. Угол выхода лучей головной волны на поверхность наблюдений

и кажущаяся скорость имеют постоянные значения. Отсюда следует, что годограф головной волны представляет собой прямую линию, начи­нающуюся от точки F и имеющую угловой коэффициент

(1.20)

Уравнение годографа головной волны

(1.21)

где - точка пересечения продолжения годографа с осью времен. Значение можно определить через координаты точки F ( [5], стр. 168)

(1.22)

Необходимо отметить, что угол берется со знаком "+" по падению пласта и со знаком "-" - по восстанию, т.е. кажущаяся ско­рость головной волны по восстанию пласта выше, чем по падению, мо­жет равняться и может принимать даже отрицательные значения.

В случае горизонтальной границы

(1.23)

кажущаяся скорость головной волны равна скорости во второй среде.

В интервале 0В головная волна Г₁ не существует, в интервале ВС она приходит позже прямой волны, при x > С головная волна Г₁ приходит раньше всех других волн - это область первых вступлений головной волны. На больших удалениях (x > D) в область первых вступлений могут выходить преломленные волны Г₂, Г_З и т.д. от более глубоких границ.

Годограф отраженной волны в горизонтально-слоистой среде.

Пока мы рассматривали простейший случай, когда покрывающая толща однородная и изотропная. В действительности же скорость в покрывающей толще может меняться скачком или плавно, как в верти­кальном, так и в горизонтальном направлениях, а также может зависеть от направления распространения волны (в анизотропных средах).

Следующим приближением к реальным средам является горизонталь­но-слоистая среда. Траектории лучей отраженной волны в такой среде имеют вид, представленный на рис. 4. Уравнения годографа можно записать в параметрической форме ( [5] , стр. 178):

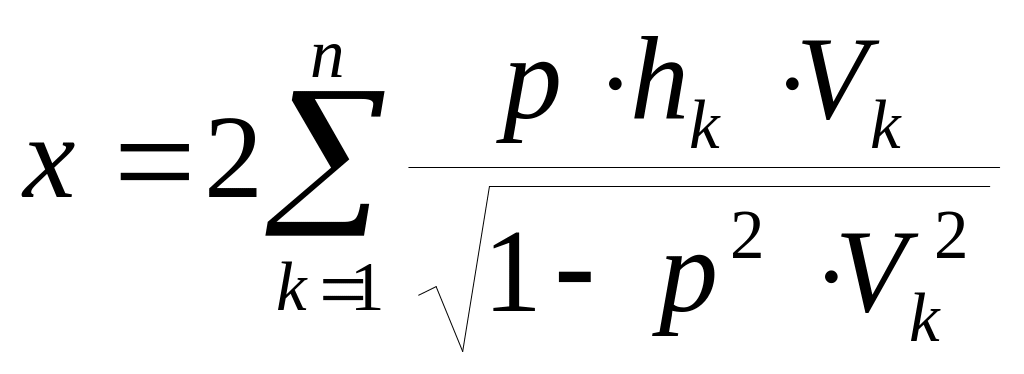(1.24)

(1.25)

где , - скорость в k-ом пласте.

В точке возбуждения ( , )

(1.26)

Годограф симметричен относительно пункта возбуждения. Кажущая­ся скорость уменьшается по мере увеличения расстояния от источника, от бесконечности до наибольшей из пластовых скоростей

Годограф рефрагированной волны.

По современным представлениям головные волны в реальных сре­дах имеют незначительную интенсивность, а в первых вступлениях часто регистрируются рефрагированные волны, которые возникают при плавном возрастании скорости с глубиной (рис. 5).

В общем случае, для произвольного закона изменения скорости с глубиной, уравнения лучей и годографов могут быть записаны лишь в параметрическом виде. Для линейного закона изменения скорости мож­но представить уравнения лучей и годографа аналитически в зависи­мости от .

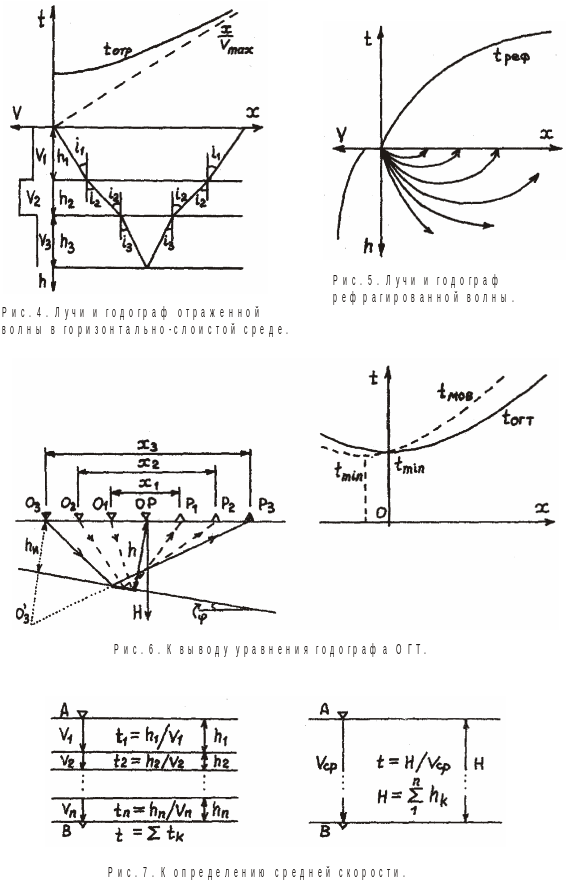
Пусть скорость изменяется с глубиной по закону:

(1.27)

где - скорость вблизи поверхности земли,

- коэффициент, размерность его [ ] .

Тогда уравнение годографа прямой рефрагированной волны будет иметь вид:

(1.28)

Можно записать уравнения годографов отраженной и головной волн для случая линейного закона изменения скорости с глубиной ( [7] , стр. 115).

Для многих реальных сред кинематические параметры головных и рефрагированных волн близки. Поэтому иногда наблюденные годо­графы рефрагированных волн ошибочно интерпретируют как годографы головных волн. Однако в некоторых случаях слабой рефракции можно допускать это и специально, так как аппарат интерпретации годо­графов головных волн более простой и удобный, а разница в резуль­татах построения может быть не существенной [§ 10].

Близость кинематических параметров головных и рефрагированных волн приводит также к очень важному практическому выводу: методика приема и регистрации этих волн одинаковая, и практически существу­ет единый метод, использующий эти два типа волн - метод преломлен­ных волн (МПВ).

Годограф общей глубинной точки.

В настоящее время широкое распространение в сейсморазведке получил метод общей глубинной точки (МОГТ), или методика многократ­ных перекрытий. Для наблюдений методом общей глубинной точки источ­ник и приемник постепенно удаляют от некоторой средней точки OP в противоположные стороны (рис. 6), и многократно возбуждают коле­бания. В случае горизонтальной границы приемник каждый раз будет принимать волну, отраженную от одной и той же точки границы. Отсю­да и появилось название метода. В случае наклонной границы отраже­ние волн происходит не от одной точки, а от некоторой площадки, но размеры площадки при этом значительно меньше, чем при наблюдениях в том же интервале профиля при фиксированном пункте возбуждения. Благодаря этому записи МОГТ оказываются более удобными для подчер­кивания полезных волн и подавления волн-помех в процессе обработки их на ЭВМ. Уравнение годографа ОГТ легко получить из уравнения го­дографа отраженной волны (1.17), если фиксированное значение глу­бины h заменить на переменное значение глубины под пунктом воз­буждения в МОГТ

Подставляя

где - эхо-глубина границы в центральной точке, получаем

(1.29)

где - время минимума годографа,

- фиктивная или эффективная скорость ОГТ.

Годограф ОГТ, вне зависимости от наклона границы, представля­ет собой гиперболу, абсцисса минимума которой равна нулю (рис. 6). Крутизна годографа определяется, кроме глубины залегания границы и скорости в покрывающей толще, также и углом наклона границы.