Глава 2 основы теории сигналов

1. Математическое представление сигналов

1.1 Сообщения, сигналы и помехи как случайные процессы

Детерминированное сообщение не содержит никакой информации. Источник информации рассматривается как устройство, осуществляющее выбор из некоторого множества возможных сообщений.

Сообщение возникает с определенной вероятностью. Множество, на котором задана вероятностная мера, называется ансамблем. Ансамбль {x(t)} функций времени есть случайный процесс. Входящая в него функция x(t) называется выборочной функцией или реализацией случайного процесса [8].

Для переноса информации необходимо установить соответствие между каждым сообщением из ансамбля и определенной реализацией сигнала. Помехи воздействуют на сигнал и по сигналу о сообщении можно судить с определенной вероятностью.

Сообщение, сигнал, помеха являются случайными процессами, которые задаются на конечном отрезке времени.

Скалярный случайный процесс может быть задан вероятностью того, что x(t) в моменты времени t₁,t₂,…t_n, не превышает значений x₁,x₂,…,x_n (см. рис.2.1.) [9]:

.

Случайная величина x(t_k) - есть сечение случайного процесса.

Рис.2.1

Если существуют частные производные функции распределения вероятностей по x_i, i=1,2,…,n, то можно определить n–мерную плотность распределения вероятностей

.

Например, достаточно распространенным сигналом является сигнал, плотность которого имеет вид

,

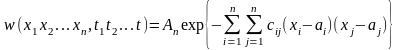где A_n, c_ij, a_i, a_j - некоторые постоянные. При n=1 одномерная плотность распределения имеет вид (нормальное распределение)

.

Среднее значение процесса по ансамблю (математическое ожидание) определится формулой

,.

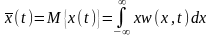где w(x,t) - одномерная плотность распределения для сечения t.

Разность между случайным процессом и его математическим ожиданием называют центрированным процессом и обозначают .

Математическое ожидание квадрата центрированного процесса называется дисперсией и определяется формулой

.

Функцией корреляции (автокорреляции) B_x(t₁,t₂) называется математическое ожидание произведения двух сечений центрированного случайного процесса в точках t₁ и t₂

,

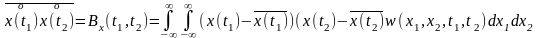где w(x₁,x₂,t₁,t₂) - двумерная плотность распределения сечения по t₁ и t₂.

Функция взаимной корреляции двух случайных процессов определится формулой

,

где w(x₁,y₂,t₁,t₂) - двумерная плотность распределения сечения по t₁ процесса X и сечения по t₂ процесса Y.

Случайный процесс, у которого математическое ожидание и дисперсия не зависят от t, а функция корреляции зависит от =t₂-t₁ и не зависит от t₁ и t₂, называется стационарным.

Помимо средних значений по ансамблю, можно определить средние значения случайного процесса по времени. Для финитного случайного процесса, заданного на (t₁,t₂), постоянная составляющая определится по формуле [10]

.

Если случайный процесс задан на (t,), то в этом случае

.

Процесс называется переменной составляющей.

Среднее по времени значение квадрата переменной составляющей

также является случайной величиной, не зависящей от t, и называется мощностью переменной составляющей.

Стационарные процессы называют эргодическими, если для них усреднение во времени приводит к тем же результатам, что и статистическое усреднение. Математическое ожидание для этих процессов равно постоянной составляющей, а дисперсия равна мощности переменной составляющей. Грубо говоря, эргодичность процесса состоит в том, что все его реализации похожи друг на друга. Функция коррекции эргодического процесса вычисляется по одной реализации усреднением во времени:

.

Функция корреляции стационарного случайного процесса имеет обозначение B_x(), где  - разность между двумя сечениями. Функция симметрична, т.к.

.

При =0 значение функции автокорреляции равно дисперсии

.

При любом  B_x()D{x(t)}, т.е. B_x() максимальна при =0.

Нормированная функцией корреляции или коэффициент корреляции случайного процесса x(t) определится

.

Для случайного стационарного процесса R_x()=B_x()/D{x(t)}, R_x()=R_x(-),R_x(0)=1, R_x()1.

Величина R_x() является в известной степени мерой статистической зависимости между сечениями процесса, отстоящими на интервале .