Завдання №2.

Тема: Метод координат. Пряма лінія на площині.

Завдання: задані вершини А(х₁,у₁), В(х₂,у₂), С(х₃,у₃) трикутника.

Знайти :

1. Рівняння сторони АВ;

2. Рівняння медіани, яка проходить через вершину С;

3. Рівняння висоти, яка проходить через вершину С;

4. Довжину висоти, проведеної через вершину с;

5. Кут В трикутника АВС;

6. Побудувати малюнок.

Зразок розв’язування завдання:

Задано трикутник АВС координатами своїх вершин А(2;2), В(5;8), С(7;1).

1.Запишемо рівняння в’язки прямих, які проходять через точку А за формулою у-у_А=k(х-х_А). У нашому випадку: у-2=k_АD(х-2). З умови перпендикулярності AD i AB одержуємо, що k_AD=-1/k_BC. Для знаходження кутового коефіцієнта k_BC запишемо рівняння сторони АВ, як прямої яка проходить через дві точки: - рівняння сторони ВС. Якщо змінну у виразити через х, то отримаємо: .

Звідси k_BC=-7/2, а отже k_AD=2/7. Тому рівняння висоти має вигляд

.

Довжину висоти AD знайдемо як відстань від точки А(2;2) до прямої ВС (7х+2у-51=0) за формулою:

. Тоді в нашому завданні матимемо такий результат .

в) Медіана СЕ ділить сторону АВ трикутника АВС навпіл, тому

отже, точка E(3,5; 5 ) – середина відрізка АВ .Запишемо рівняння медіани СЕ, як рівняння прямої , яка проходить через дві точки С(7;1) і Е(3,5; 5).

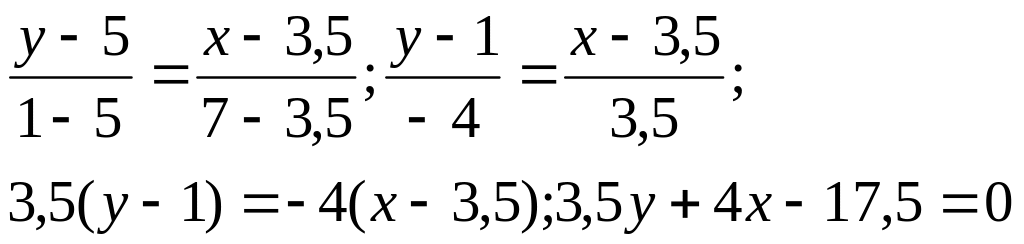
г)значення кута В знаходимо за формулою рахуючи кут від прямої з кутовим коефіцієнтом k₁ до прямої з кутовим коефіцієнтом k₂ проти годинникової стрілки. Обчислюємо кутові коефіцієнти сторін:

Звідси B=arctg 0,916. д)площу трикутника АВС знаходимо за формулою: S_ABC=

Довжину сторони ВС знаходимо за формулою:

Довжину сторони ВС знаходимо як відстань між двома точками

d=

S_ABC=

BC=

S_ABC= (кв.од).

Завдання для самостійного виконання:

1. А(10;2), В( 2; 8), С(3;3);

2. А(6;4), В(- 2; 2), С(8;-3);

3. A(7;3), В( -1; 9), С(0;4);

4. А(12;-2), В( 4; 4), С(5;-1);

5. А(7;5), В(-1; 9), С(-3;-2);

6. А(8;3), В( 0; 9), С(1;4);

7. А(6;3), В(- 2; 9), С(-3;-1);

8. А(13;3), В( 5; 9), С( 6; 4);

9. А(5;-1), В( -3; 5), С(-2; 0);

10. А( 6;2), В( -2; 8), С( -1;3);

11. А(11;0), В( 3; 6), С( 4; 1);

12. А(6;6), В( -2; 12), С( 0;2);

13. А( 2;-1), В( -6; 5), С( -1; -3);

14. А( -3;2), В( 5; -4), С( 4; 0);

15. А( 3; 3), В( -5; 9), С(-3;-1);

16. А( 4; 8), В( -4; 2), С( 2; -2);

17. А( -2; 0), В( 2; 4), С( 4; 0);

18. А( -2; 0), В( 2; 6), С( 4; 2);

19. А(14;-1), В( 6; 5), С( 7;0);

20. А(0;7), В( 6; -1), С ( 2; 1);

21. А(10;8), В( -2; 8), С(-3;-3);

22. А(1;5), В( 12;- 8), С( 6; 4);

23. А(0;8), В( 1; 7), С(5;3);

24. А(8;6), В( 4; 8), С( 6;3);

25. А(-4; 4), В( 3; -1), С( 7;2);

26. А( 4;1;), В(2;-3) , С( 3;-5);

27. А( 4;4), В(0;0) , С( 0;6);

28. А( 2;5), В(-2;-6) , С( 2; 2;);

29. А( -5;-4), В( -5; 6) , С(- 3;-4);

30. А(-7; 1), В(2;-1) , С( -1;-5);

Завдання № 3

Тема. Границі функції. Знаходження границь функцій.

Розкриття невизначеностей.

Приклад.

Знайти границю:

.

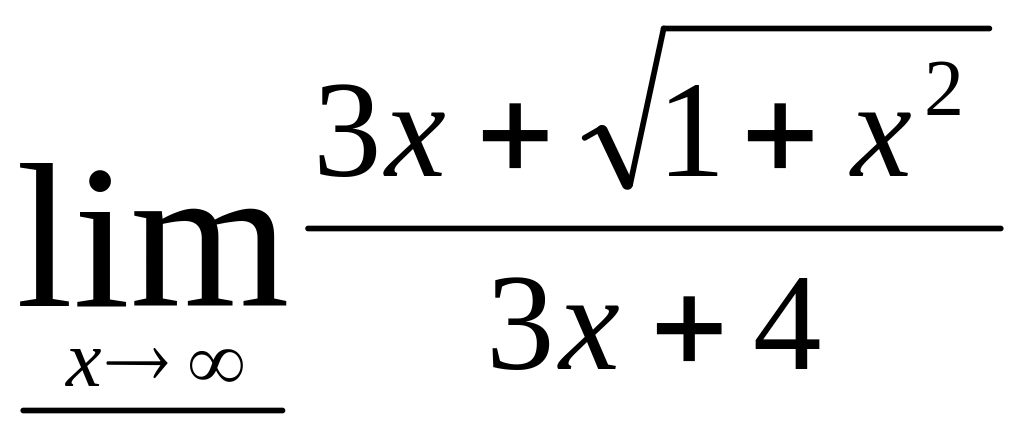Розділивши знаменник і чисельник на х, одержимо

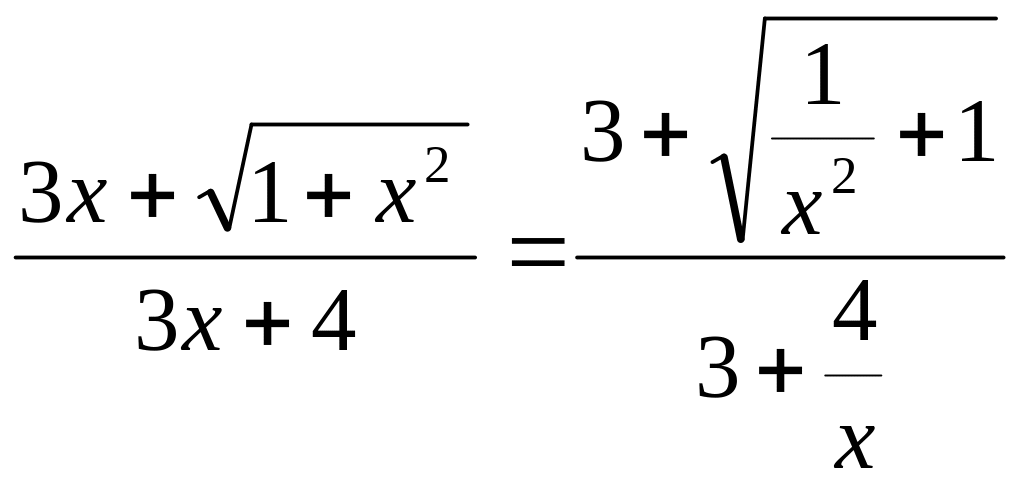. Дальше переходимо до границі, коли х ∞