3. Системи числення

Система числення – це спосіб представлення чисел і відповідні йому правила дії над числами. Різноманітні системи числення, які існували раніше і які використовуються у наш час, можна розділити на непозиційні та позиційні. Знаки, які використовуються під час запису чисел, називаються цифрами.

У непозиційних системах числення від положення цифри в запису числа не залежить величина, яку вона позначає.

Прикладом непозиційної системи числення є римська система (римські цифри). У римській системі замість цифр використовуються латинські літери:

I V X L С D М

1 5 10 50 100 500 1000

Приклад 1. Число ССХХХП складається з двох сотень, трьох десятків і двох одиниць, та дорівнює двомстам тридцяти двом.

У римських числах цифри записуються зліва направо у порядку убування. У такому разі їх значення складаються. Якщо ж зліва записана менша цифра, а праворуч – велика, то їх значення віднімаються.

Приклад 2

VI = 5 + 1 = 6, а IV = 5–1 = 4.

Приклад 3

MCMXCVIII = 1000 + (–100 + 1000) + (–10 + 100) + 5 +1 +1 +1 = = 1998.

У позиційних системах числення величина, позначається цифрою в запису числа, залежить від її позиції. Кількість використаних цифр називається основою позиційної системи числення. Система числення, застосовувана в сучасній математиці, є позиційною десятковою системою. Її основа дорівнює десяти, тому що запис будь-яких чисел проводиться за допомогою десяти цифр:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Позиційного характеру цієї системи легко зрозуміти на прикладі будь-якого багатозначного числа. Наприклад, в числі 333 перша трійка означає три сотні, друга – три десятки, третя – три одиниці.

Для запису чисел в позиційній системі з основою n потрібно мати алфавіт з n цифр. Зазвичай для цього при n <10 використовують n перших арабських цифр, а при n> 10 до десяти арабським цифрам додають літери. Ось приклади алфавітів кількох систем:

Основа вимагається вказати основу системи, до якої відноситься число, то воно приписується нижнім індексом до цього числа. Наприклад: Якщо вімагається вказаті основу системи, до якої відносіться число, то воно пріпісується ніжнім індексом До цього числа. Наприклад: По–украински (Редактировать) Основа	Назва	Алфавіт
n = 2	двійкова	01
n = 3	трійкова	012
n = 8	вісімкова	01234567
n=16	шістнадцяткова	0123456789ABCDEF

Якщо необхідно вказати основу системи, до якої відносіться число, то воно приписується нижнім індексом до цього числа. Наприклад:

101101₂, 3671₈, 3B8F₁₆.

У системі числення з основою q (q-ічная система числення) одиницями розрядів служать послідовні ступені числа q. q одиниць будь-якого розряду утворюють одиницю наступного розряду. Для запису числа в q-ічній системі числення потрібно q різних знаків (цифр), що зображують числа 0, 1, ..., q–1. Запис числа q в q-ічной системі числення має вигляд 10.

Розгорнутою формою запису числа називається запис у вигляді

A_q=(a_n–1q^n–1+a_n–2q^n–2++a₀q⁰+a_–1q^–1+a_–2q^–2++a_–mq^–m).

Маємо А_q – саме число, q – заснування системи числення, a_i – цифри даної системи числення, n – число розрядів цілої частини числа, m – число розрядів дробової частини числа.

 

Приклад 4. Отримати розгорнуту форму десяткових чисел 32478; 26,387.

32478₁₀ = 3 * 10000 + 2 * 1000 + 4 * 100 + 7 * 10 +

+ 8 = 3 * 10⁴ + 2 * 10³ + 4 * 10² + 7 * 10¹ + 8 * 10°.

26,387₁₀ = 2 * 10¹ + 6 * 10° + 3 * 10^–1 + 8 * 10^–2 + 7 * 10^–3.

Зверніть увагу, що в будь-якій системі числення її основа записується як 10.

Якщо всі складові в розгорнутій формі недесятічного числа представити в десятковій системі і обчислити отриманий вираз за правилами десяткової арифметики, то вийде число в десятковій системі, рівне даному. За цим принципом проводиться переклад з не десяткової системи в десяткову.

Переклад цілих чисел.

1. Основу нової системи числення виразити в десятковій системі числення і всі подальші дії робити в десятковій системі числення;

2. послідовно виконувати поділ даного числа і одержуваних неповних часток на основу нової системи числення до тих пір, поки не отримаємо неповну частку, менше дільника;

3. отримані залишки, які є цифрами числа в новій системі числення, привести у відповідність з алфавітом нової системи числення;

4. скласти число в новій системі числення, записуючи його починаючи з останнього залишку.

Приклад 1. Провести число 3710 в двійкову систему.

Для позначення цифр у записі числа використовуємо символіку:

а₅а₄а₃а₂а₁а₀

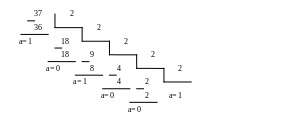
Звідси: 37 = 100101

Приклад 2. Привести десяткове число 315 до вісімкової та шістнадцяткової системи:

Звідси: 315 = 473 = 13В .

Нагадаємо, що 11 = В .

Переклад дробових чисел.

1) Основу нової системи числення виразити в десятковій системі і всі подальші дії робити в десятковій системі числення;

2) послідовно множити дане число і отримані дробові частини добутків на основу нової системи до тих пір, поки дробова частина добутку не стане рівною нулю або не буде досягнута необхідна точність представлення числа в новій системі числення;

3) отримані цілі частини добутків, які є цифрами числа в новій системі числення, привести у відповідність з алфавітом нової системи числення;

4) скласти дробову частину числа в новій системі числення, починаючи з цілої частини першого добутку.

Приклад 3. Провести десяткову дріб 0,1875 у двійкову, вісімкову та шістнадцяткову системи.

Тут вертикальна межа відокремлює цілі частини чисел від дрібних частин.

Звідси: 0,1875₁₀ = 0,0011₂ = 0,14₈ = 0,3₁₆.

Переклад змішаних чисел, що містять цілу і дробову частини, здійснюється у два етапи. Ціла та дробова частини вихідного числа переводяться окремо за відповідними алгоритмами. У підсумковому запису числа, в новій системі числення, ціла частина відділяється від дробової комою (крапкою).

Приклад 4. Провести десяткове число 315,1875 в вісімкову та в шістнадцяткову системи числення. З розглянутих вище прикладів слід: 315,1875₁₀ = 473,14₈ = 13В,3₁₆.

Переклад з двійкової в десяткову:

110100101₂ = 1*10₂⁸+1*10₂⁷+ 0*10₂⁶+1*10₂⁵+0*10₂⁴+0*10₂³+ 1*10₂²+0*10₂¹+1*10₂⁰= 1*2₁₀⁸+1*2₁₀⁷+0*2₁₀⁶+1*2₁₀⁵+ 0*2₁₀⁴+0*2₁₀³+1*2₁₀²+0*2₁₀¹+ 1*2₁₀⁰=421₁₀

Рішення задач.

Рішення задач на дошці з групою.

Завдання:

№ 1

Які числа записані за допомогою римських цифр:

MMMD, IV, XIX, MCMXCIVII?

№ 2

Запищіть рік, місяць і число свого народження з допомогою римських цифр.

№ 3

Виконайте дії і запишіть результат римськими цифрами:

XXII–V; CV–LII; XX: V; X × IV;

№ 4

Запишіть перші 20 чисел натурального числового ряду в двійковій системі числення.

№ 5

Провести цілі числа з десяткової системи числення в двійкову:

1) 523; 65; 7000; 2307; 325;

2) 12; 524; 76; 121; 56.

№ 6

Представити десяткові дробі в двійкову систему числення. У двійковому запису числа зберегти шість знаків.

1) 0,654; 0,321; 0,6135; 0,9876;

2) 0,555; 0,333; 0,1213; 0,453.

№ 7

Перевести змішані десяткові числа в двійкову та восьмирічну системи числення, залишивши п'ять знаків у дробовій частині нового числа:

1) 21,5; 432,54; 678,333;

2) 12,25; 97,444; 7896,2.

№ 8

Перекласти з десяткової системи числення наступні числа:

1)345 А₅, 0,125А₈, 45,65А₄;

2) 675А₁₂, 0,333А₃, 23,15А₅.

№ 9

Перекласти з десяткової системи числення наступні числа:

1) 1,25А₁₆, 675А₇, 0,355А₄;

2) 890А₆, 0,675 А₈, 12,35А₇.

№ 10

Перекласти з десяткової системи числення наступні числа:

1) 425А₆, 0,425А₁₂, 98,45А₃;

2) 0,55Ад, 765А₃, 765,75А₄.

Домашнє завдання.

№ 1

Перекласти з десяткової системи числення наступні числа:

1) 98А₂, 0,545А₁₆, 87,325А₈;

2) 0,755А₅, 907А_б, 566,225А₁₆.

№ 2

Виконайте дії і запишіть результат римськими цифрами:

IC + XIX; МСМ + VIII;

LXVI: XI; XXIV · VII